Разработке урока "Геометрический смысл производной функции" позволяет:
1. Ввести понятие физический смысл производной функции.
2. Повторить понятия линейная функция, угловой коэффициент прямой.
3. Дать определения секущей и касательной к графику функции.
4.Ввести понятие геометрический смысл производной функциии.
5. Научиться находить значение производной функции по графику функции.
Просмотр содержимого документа
«Геометрический смысл производной функции»

ФИЗИЧЕСКИЙ СМЫСЛ
ПРОИЗВОДНОЙ

Мгновенная скорость – величина пути за мгновение

Мгновенная скорость движения
Если s (t) - закон прямолинейного движения тела, то производная
выражает мгновенную скорость в момент времени t .

1

2

3

Определение
Функция заданная с помощью формулы у=кх+b называется линейной.
Число k=tg называется угловым коэффициентом прямой.
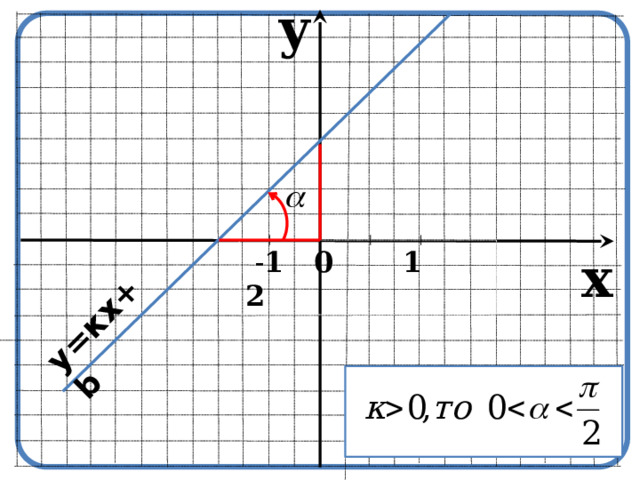
y
y=кх+b
- 1 0 1 2
x
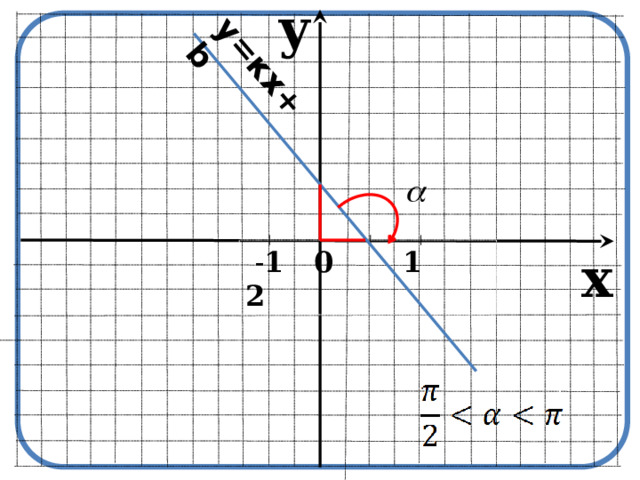
y
y=кх+b
- 1 0 1 2
x
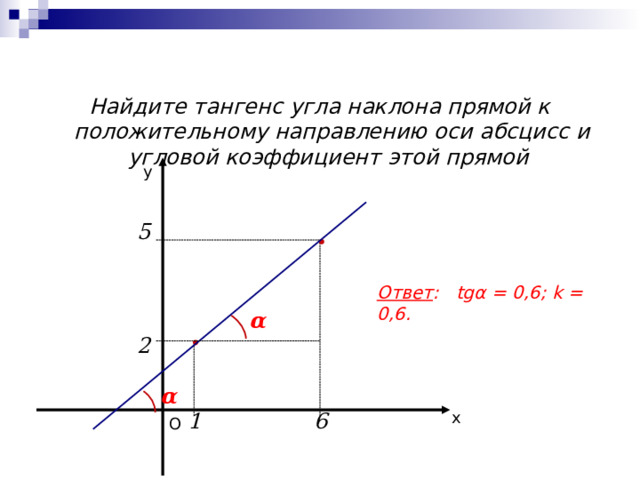
Найдите тангенс угла наклона прямой к положительному направлению оси абсцисс и угловой коэффициент этой прямой
у
5
Ответ : tgα = 0,6; k = 0,6.
α
2
α
х
6
1
О
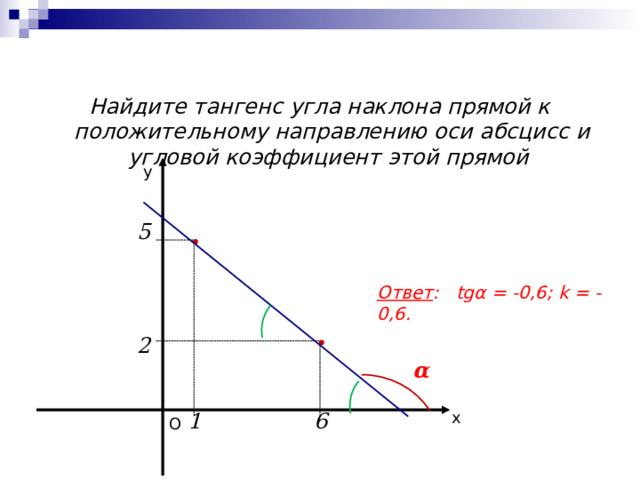
Найдите тангенс угла наклона прямой к положительному направлению оси абсцисс и угловой коэффициент этой прямой
у
5
Ответ : tgα = -0,6; k = -0,6.
2
α
х
1
6
О
y
y=кх+b
- 1 0 1 2
x
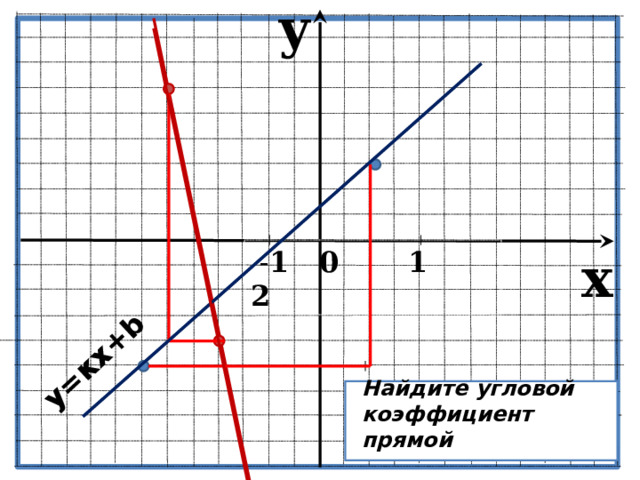
Найдите угловой коэффициент прямой
касательная
секущая
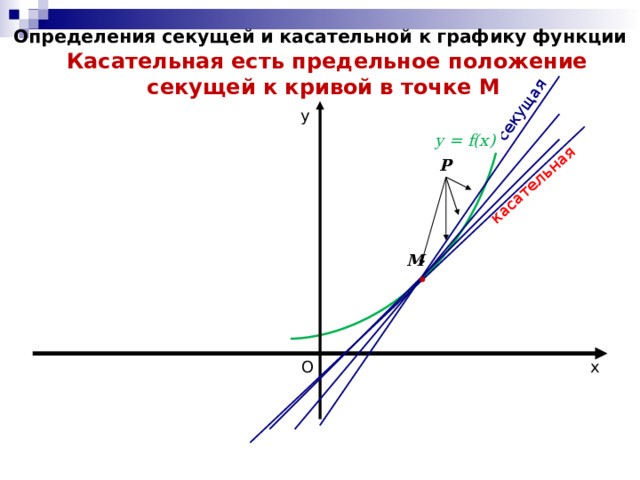
Определения секущей и касательной к графику функции
Касательная есть предельное положение секущей к кривой в точке М
у
у = f(x)
P
M
О
х
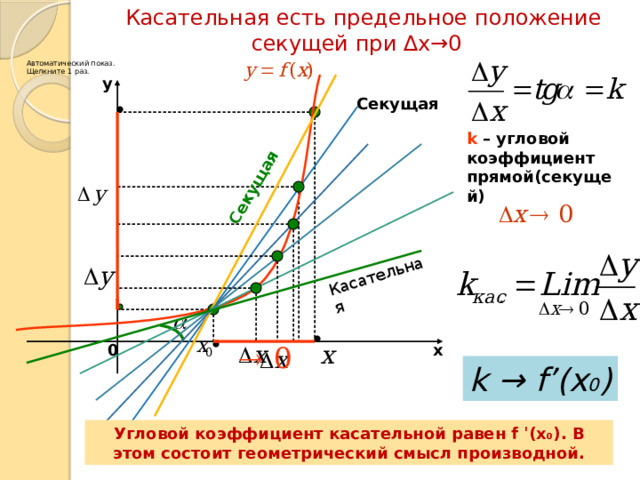
Касательная есть предельное положение секущей при ∆х →0
Секущая
Касательная
Автоматический показ. Щелкните 1 раз.
y
Секущая
k – угловой коэффициент прямой(секущей)
0
х
k → f’(x 0 )
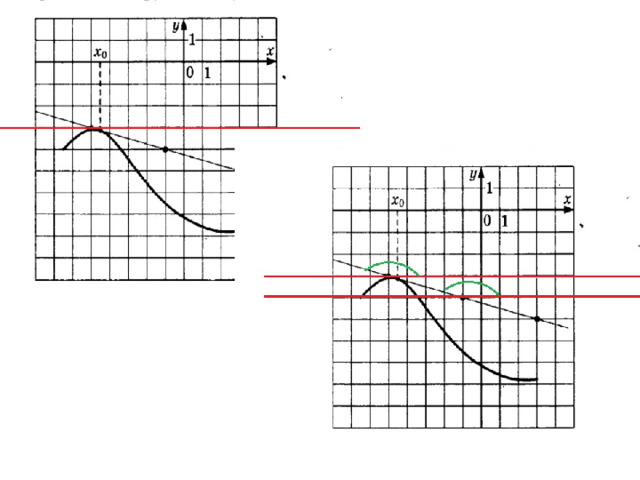
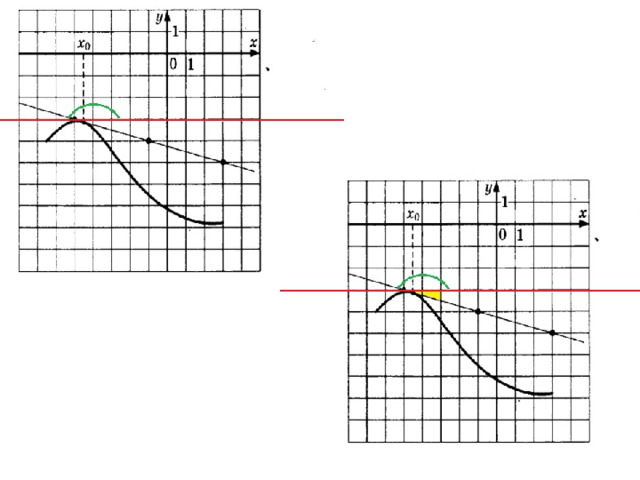
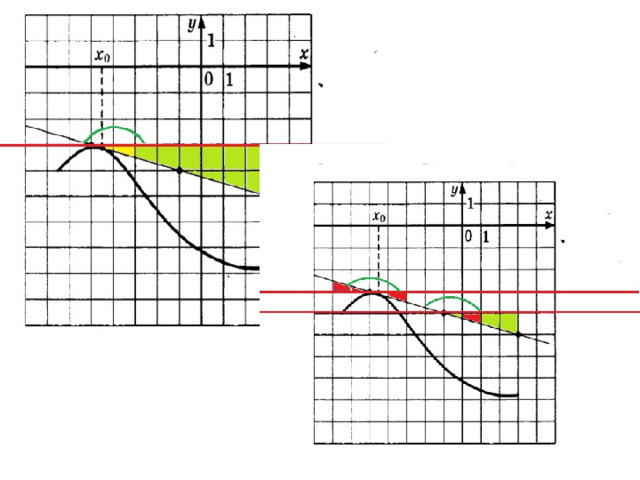
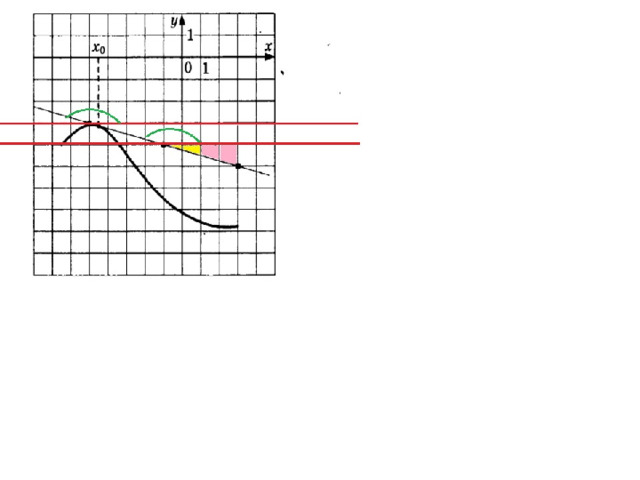
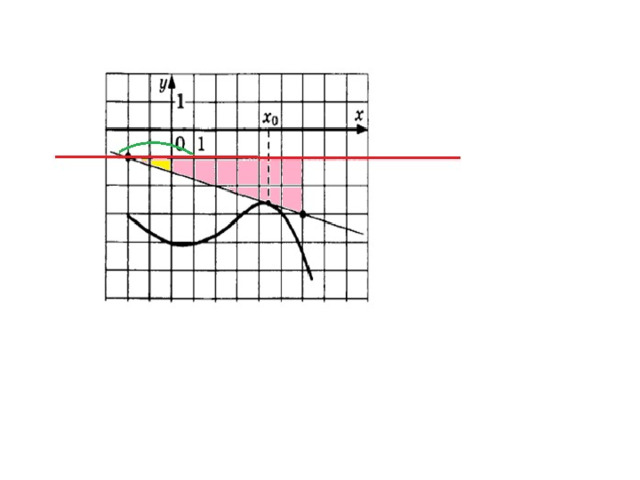
Угловой коэффициент касательной равен f ˈ(х 0 ). В этом состоит геометрический смысл производной.
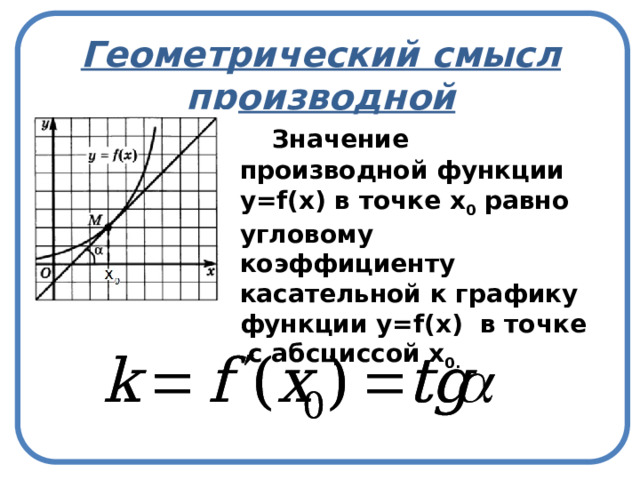
Геометрический смысл производной
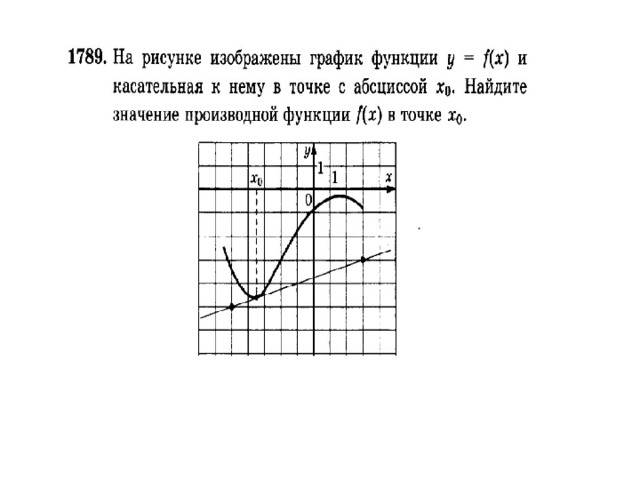
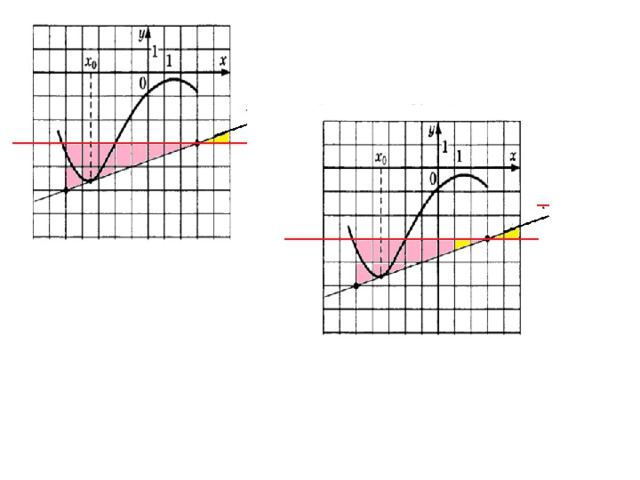
Значение производной функции y=f(х) в точке х 0 равно угловому коэффициенту касательной к графику функции y=f(х) в точке с абсциссой х 0.
14

Как связаны между собой непрерывность и дифференцируемость функции в точке?
Пусть функция дифференцируема в точке х 0, тогда к графику этой функции можно провести касательную в точке с абсциссой х 0 . Причем
Такой график не может иметь разрыв в точке с абсциссой х 0.
14
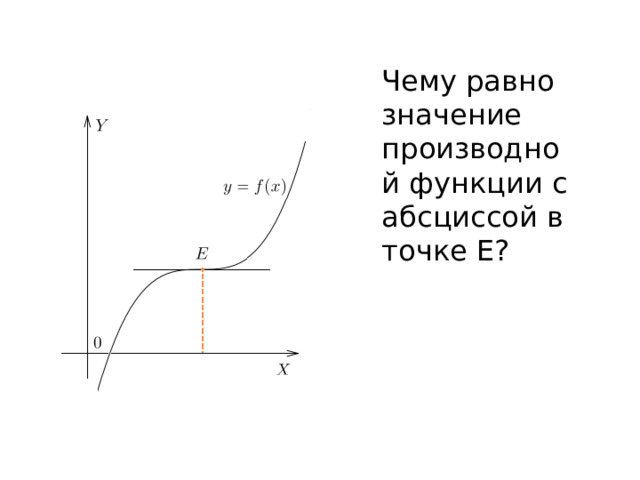
Чему равно значение производной функции с абсциссой в точке Е?
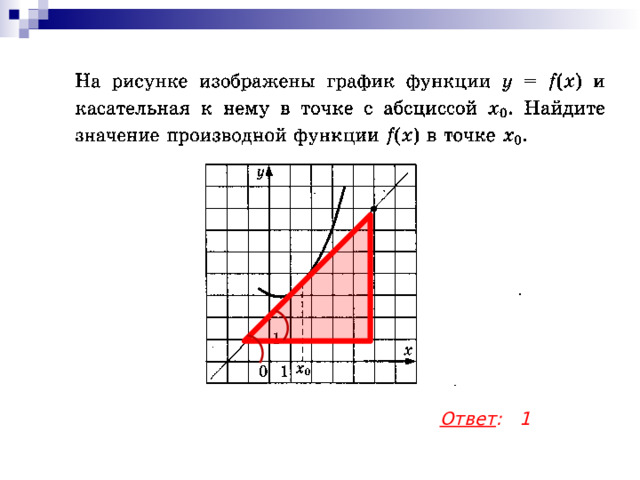
Ответ : 1
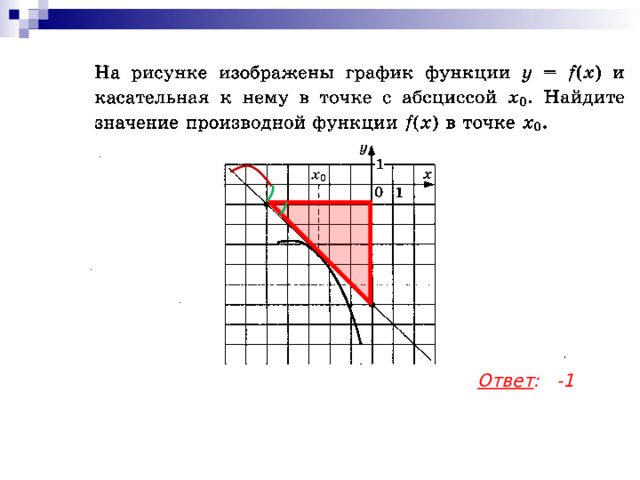
Ответ : -1
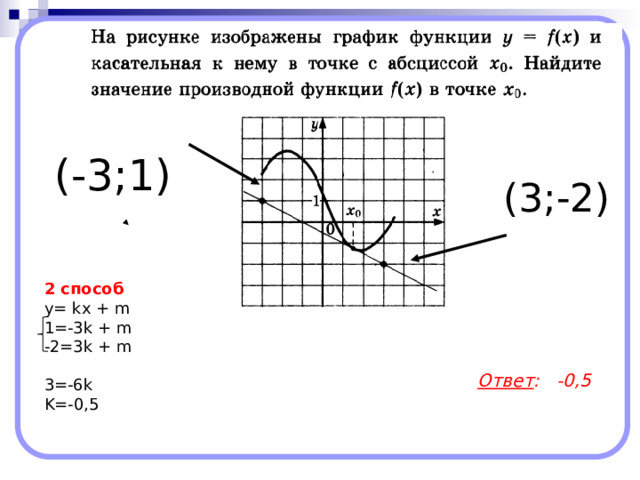
(-3;1)
(3;-2)
2 способ
у= kx + m
1=-3k + m
-2=3k + m
3=-6k
K=-0,5
Ответ : -0,5
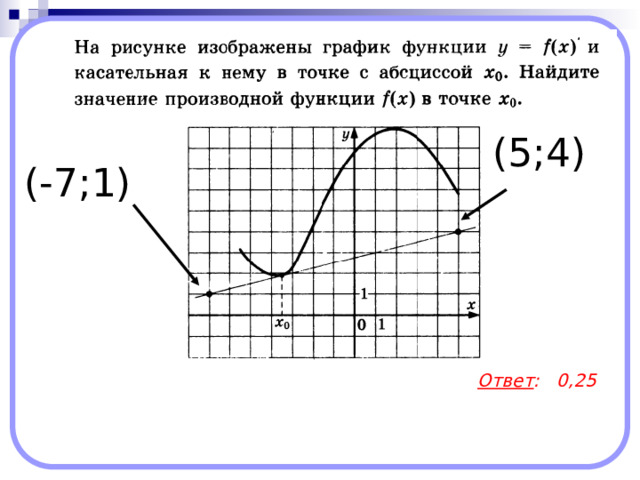
(5;4)
(-7;1)
Ответ : 0,25
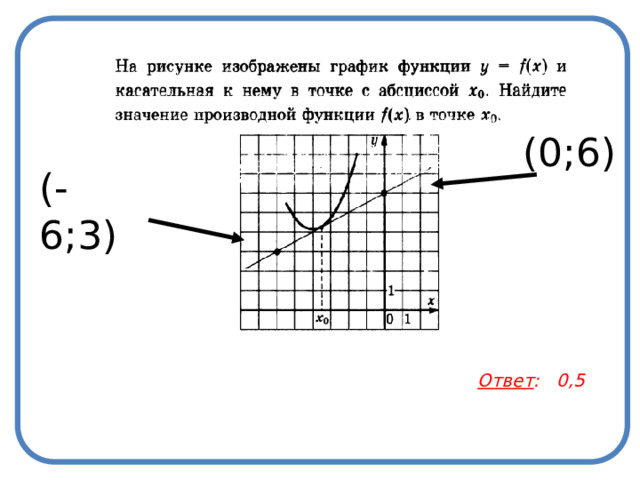
(0;6)
(-6;3)
Ответ : 0,5
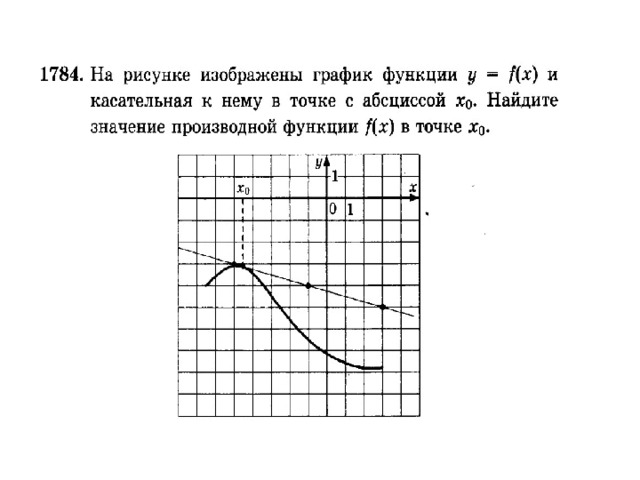

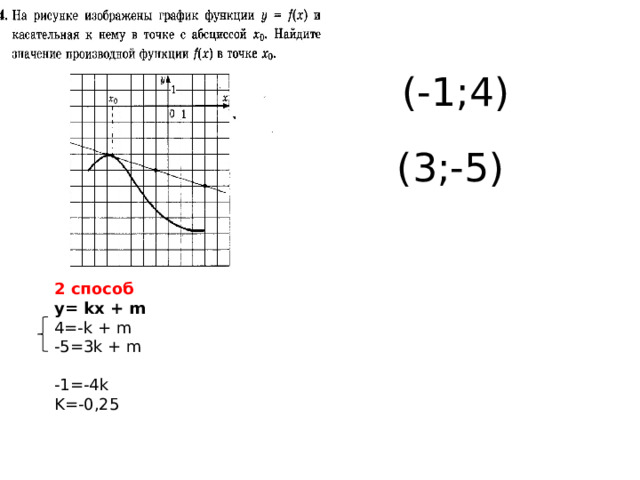
(-1;4)
(3;-5)
2 способ
у= kx + m
4=-k + m
-5=3k + m
-1=-4k
K=-0,25

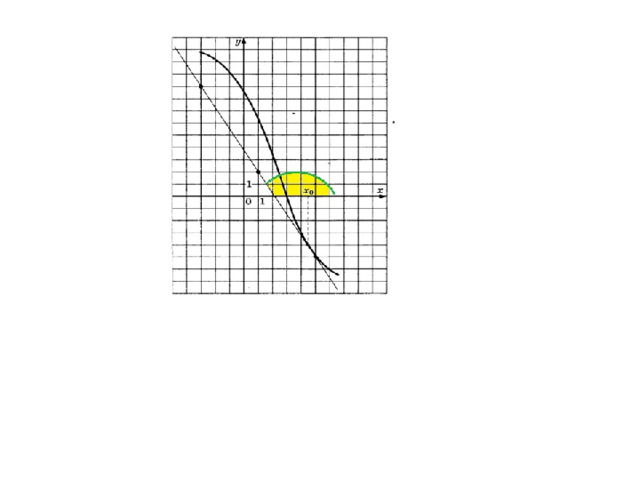
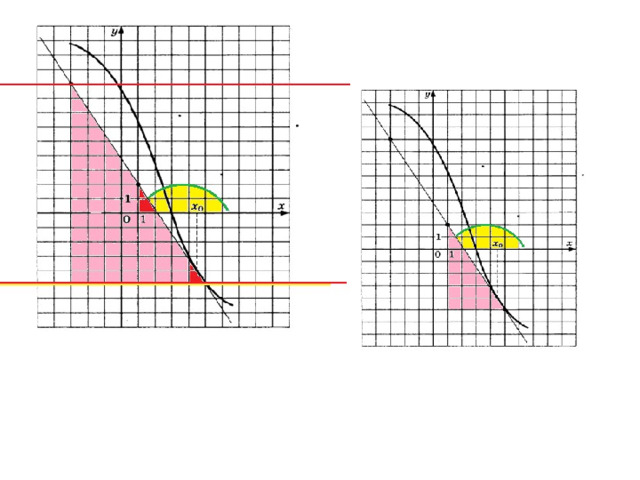
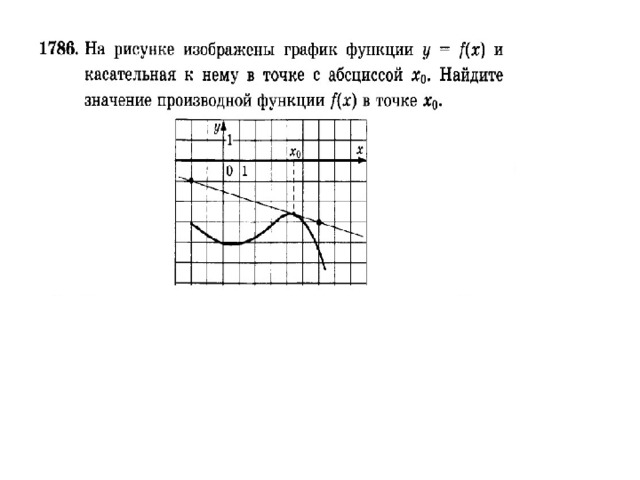
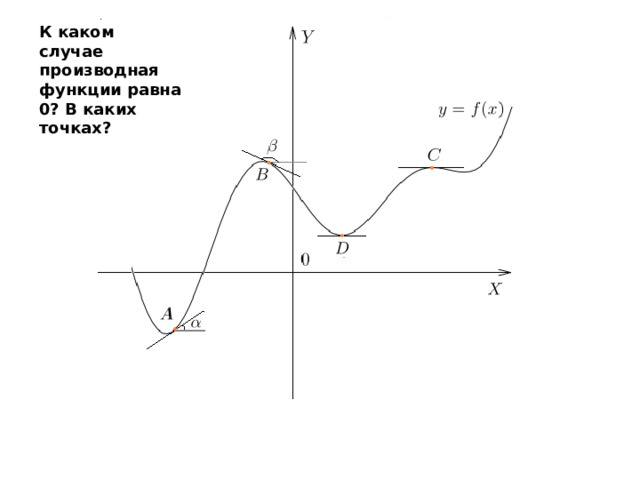
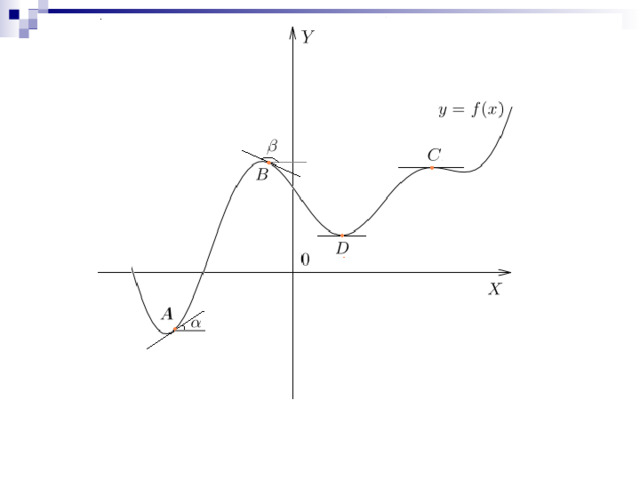
К каком случае производная функции равна 0? В каких точках?
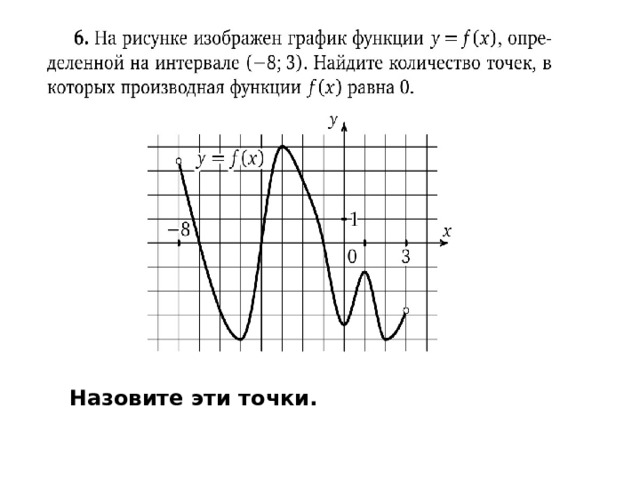
Назовите эти точки.

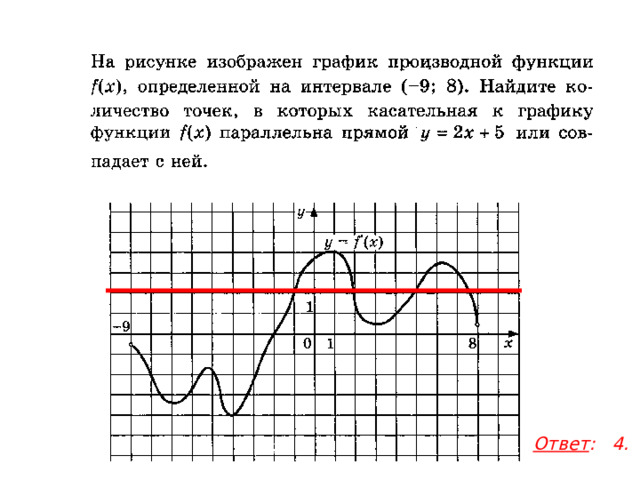
Ответ : 4.
14

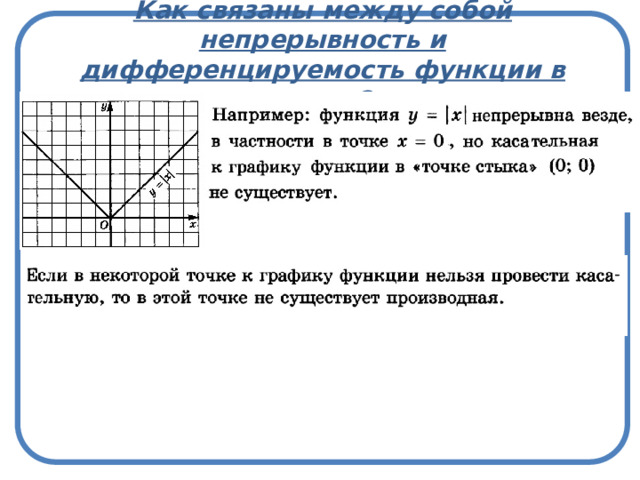
Как связаны между собой непрерывность и дифференцируемость функции в точке?
14

Как связаны между собой непрерывность и дифференцируемость функции в точке?
14
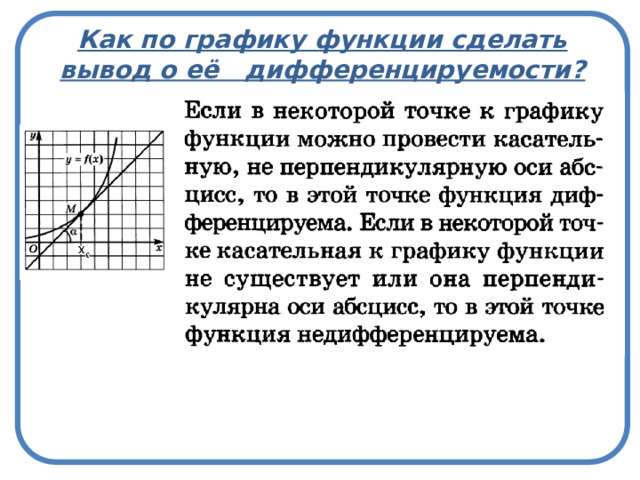
Как по графику функции сделать вывод о её дифференцируемости?
14
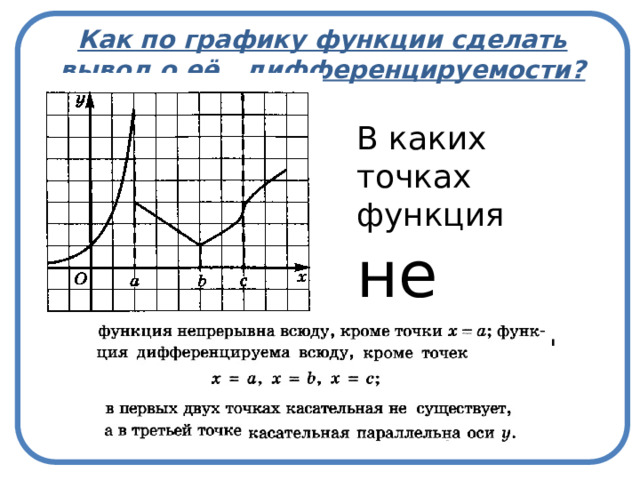
Как по графику функции сделать вывод о её дифференцируемости?
В каких точках функция не дифференцируема?
14






























































