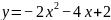Регулятивные УУД: владеть способами самопроверки, самоконтроля процесса и результата решения математической задачи; оценивать соответствие результата деятельности поставленной цели и условиям, объяснять причины достижения или недостижения цели, находить ошибку, давать оценку приобретённому опыту; принимать и сохранять учебную задачу, определять цели и формулировать задач; планировать действия в соответствии с поставленной задачей (свои и группы), выбирая наиболее эффективные способы и пути достижения целей.
Коммуникативные УУД: воспринимать и формулировать суждения в соответствии с условиями и целями общения; ясно, точно, грамотно выражать свою точку зрения в устных и письменных текстах, давать пояснения по ходу решения задачи, комментировать полученный результат; принимать цель совместной деятельности, планировать организацию совместной работы, распределять виды работ, договариваться, обсуждать процесс и результат работы; обобщать мнения нескольких людей.
Познавательные УУД: выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями; формулировать определения понятий; устанавливать существенный признак классификации, основания для обобщения и сравнения, критерии проводимого анализа.
| Этап урока | Деятельность учителя | Деятельность обучающихся | Используемые методы, приемы, формы | Формируемые УУД | Результат взаимодействия (сотрудничества) | Планируемое время |
| 1. Этап мотивации к коррекционной деятельности |
|
| - Здравствуйте, ребята. Сегодня мы с вами будем искать сокровища. Озвучить правила игры. Выдать индивидуальные маршртные листы Капитанам команды выдает конверты с номерами, внутри которых содержатся задания для первого этапа и правила. Выполнив задания очередного конверта, команда узнает номер следующего конверта. Смысл игры – последовательно выполняя задания, дойти до конверта с последним этапом, после выполнения которого детям выдается сокровища. | Поприветсвовать Разделиться на 3 команды. Выбрать капитана. Получить индивидуальные маршртные листы Прослушать правила. Капитаны команд берут конверт с заданием на первый этап. | Методы и приемы: словесный (объяснение). Формы: фронтальная.
| Регулятивные УУД: принимать и сохранять учебную задачу, определять цели и формулировать задач. Коммуникативные УУД: принимать цель совместной деятельности, планировать организацию совместной работы, распределять виды работ, договариваться, обсуждать процесс и результат работы.
| Совершенствовать умения, навыки учащихся при работе в группе.
| 3 мин |
Этап актуализации и пробного учебного действия |
|
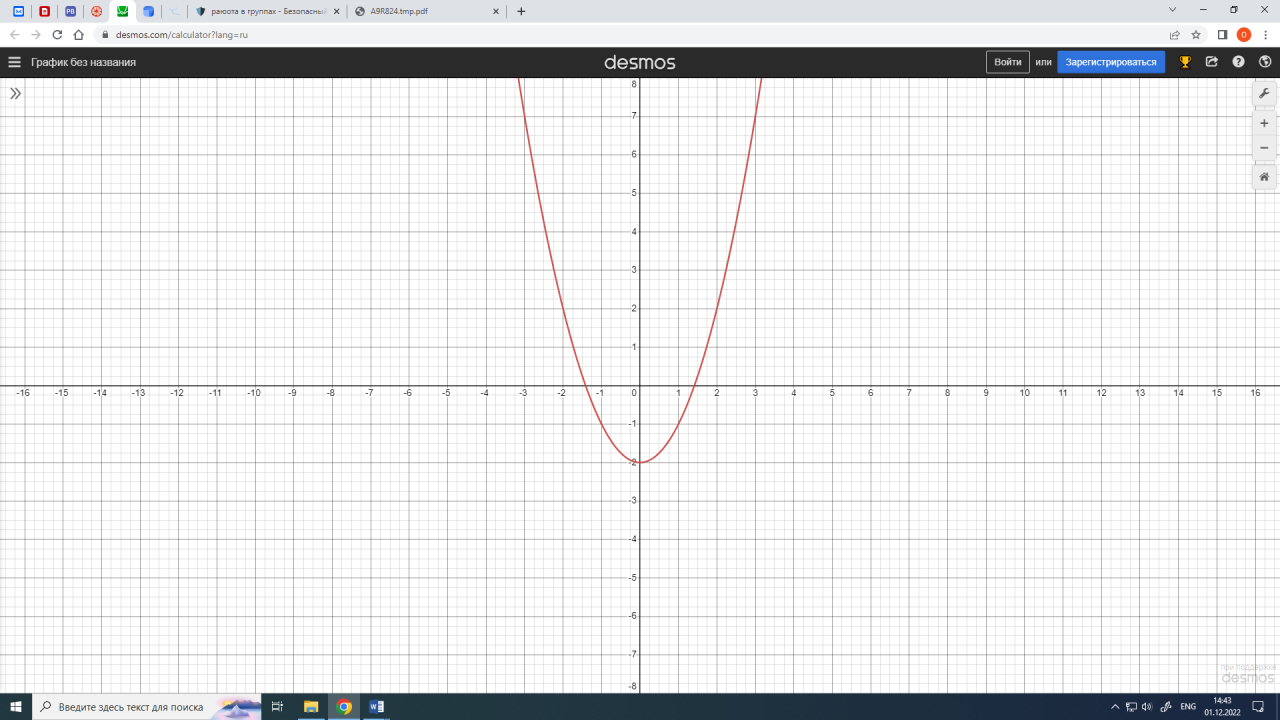
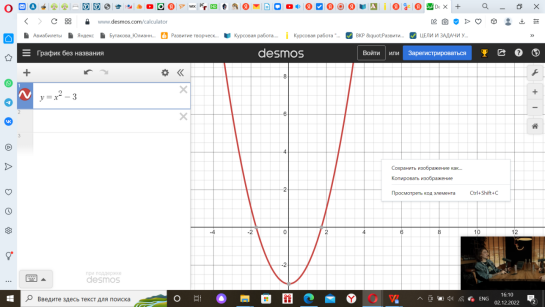
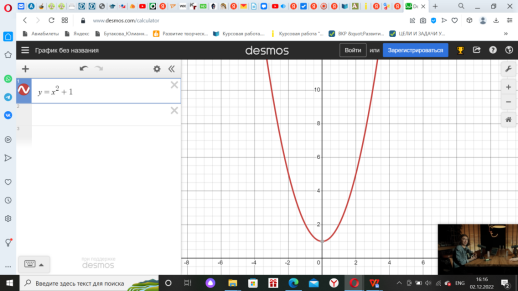
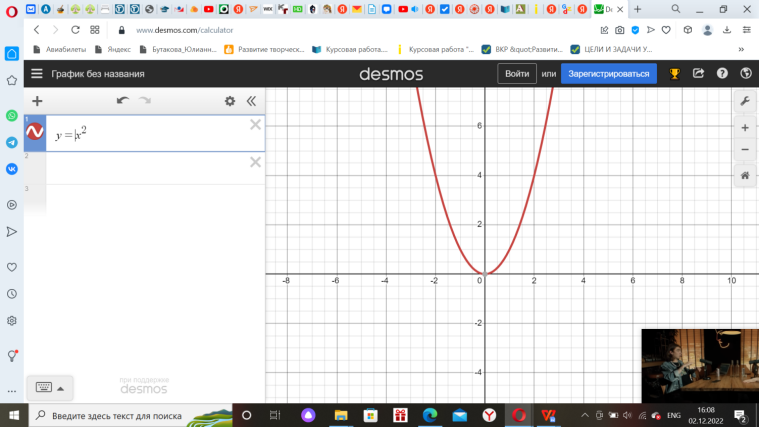
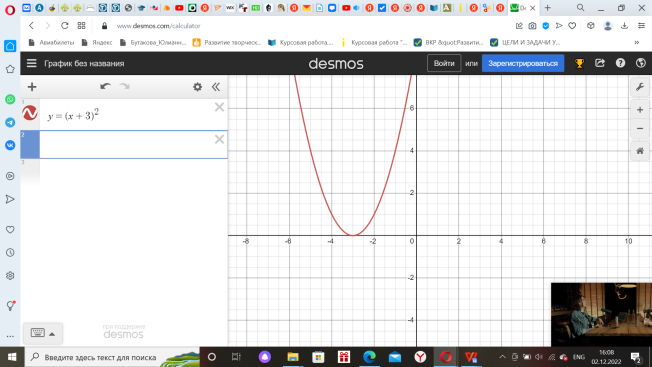
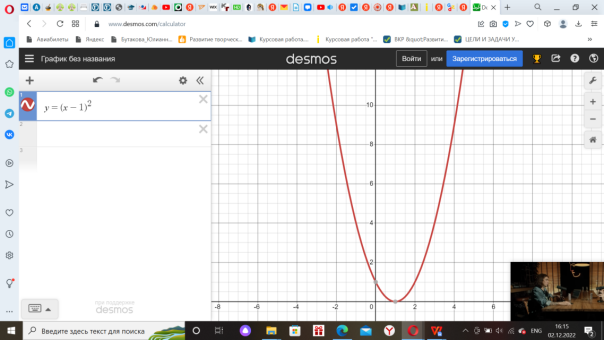
| Наблюдает за активностью детей в командах, делает отметки на листах наблюдения. | Выполняют задания по каждому этапу получают числа и берут следующие конверты. Задание 1 на свойства описанной формулой. (Приложение 1) Задание 2 на чтение графиков квадратичных функций (Приложение 2) Задание 3 на нахождение аргумента x (Приложение 3)
| Методы и приемы: практический метод (выполнение заданий). Формы: групповая. | Регулятивные УУД: планировать действия в соответствии с поставленной задачей (свои и группы), выбирая наиболее эффективные способы и пути достижения целей. Коммуникативные УУД: воспринимать и формулировать суждения в соответствии с условиями и целями общения; ясно, точно, грамотно выражать свою точку зрения в устных и письменных текстах, давать пояснения по ходу решения задачи, комментировать полученный результат; принимать цель совместной деятельности, планировать организацию совместной работы, распределять виды работ, договариваться, обсуждать процесс и результат работы; обобщать мнения нескольких людей. Познавательные УУД: выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями; формулировать определения понятий; устанавливать существенный признак классификации, основания для обобщения и сравнения, критерии проводимого анализа. | Повторить определение и свойства квадратичной функции, как влияют коэффициенты а, с и дискриминант квадратного трехчлена на расположение графика квадратичной функции; Закрепить умения построения графика квадратичной функции и нахождения: области определения и области значений функции; нулей функции; промежутков знакопостоянства и промежутков монотонности по графику квадратичной функции. Воспитывать аккуратность в работе при построении графиков. | 20 мин |
Этап локализации индивидуальных затруднений |
|
| Наблюдает за активностью детей в командах, делает отметки на листах наблюдения. | Рассматривают возникшие ошибки во время выполнения какого-то из этапов. | Методы и приемы: практический метод (выполнение заданий). Формы: групповая. | Регулятивные УУД: владеть способами самопроверки, самоконтроля процесса и результата решения математической задачи. Коммуникативные УУД: воспринимать и формулировать суждения в соответствии с условиями и целями общения; ясно, точно, грамотно выражать свою точку зрения в устных и письменных текстах, давать пояснения по ходу решения задачи, комментировать полученный результат; принимать цель совместной деятельности, планировать организацию совместной работы, распределять виды работ, договариваться, обсуждать процесс и результат работы; обобщать мнения нескольких людей. Познавательные УУД: выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями; формулировать определения понятий; устанавливать существенный признак классификации, основания для обобщения и сравнения, критерии проводимого анализа. | Развивать умения сравнивать, обобщать, делать выводы. | 2 мин |
Этап построения проекта коррекции затруднения |
|
| В случае, если дети затруднются в выполнении какого-либо задания, задает вопросы, и если обучающиеся правильно на него отвечают, выдает подсказку. | Совместно строят план решения возникших затруднений или отвечают на вопрос для получения подсказки как можно решить. | Методы и приемы: практический метод (выполнение заданий), словесный (беседа). Формы: фронтальная, групповая. | Регулятивные УУД: планировать действия в соответствии с поставленной задачей (свои и группы), выбирая наиболее эффективные способы и пути достижения целей. Коммуникативные УУД: воспринимать и формулировать суждения в соответствии с условиями и целями общения; ясно, точно, грамотно выражать свою точку зрения в устных и письменных текстах, давать пояснения по ходу решения задачи, комментировать полученный результат; принимать цель совместной деятельности, планировать организацию совместной работы, распределять виды работ, договариваться, обсуждать процесс и результат работы; обобщать мнения нескольких людей. Познавательные УУД: выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями; формулировать определения понятий; устанавливать существенный признак классификации, основания для обобщения и сравнения, критерии проводимого анализа. | Развивать у учащихся самостоятельность в мышлении и учебной деятельности.
| 2 мин |
Этап реализации построенного проекта |
|
| Наблюдает за активностью детей в командах, делает отметки на листах наблюдения. | Выходят из затруднения с помощью построенного плана и выполняют задания дальше. | Методы и приемы: практический метод (выполнение заданий). Формы: групповая. | Регулятивные УУД: владеть способами самопроверки, самоконтроля процесса и результата решения математической задачи. Коммуникативные УУД: воспринимать и формулировать суждения в соответствии с условиями и целями общения; ясно, точно, грамотно выражать свою точку зрения в устных и письменных текстах, давать пояснения по ходу решения задачи, комментировать полученный результат; принимать цель совместной деятельности, планировать организацию совместной работы, распределять виды работ, договариваться, обсуждать процесс и результат работы; обобщать мнения нескольких людей. Познавательные УУД: выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями; формулировать определения понятий; устанавливать существенный признак классификации, основания для обобщения и сравнения, критерии проводимого анализа. | Совершенствовать умения, навыки учащихся при работе в группе.
| 2 мин |
Этап обобщения затруднений |
|
| Задать вопросы после выполнения заданий: - Какие затруднения возникали? Как находили выход из затруднений? Что необходимо знать, чтобы исправить ошибки? Что не получалось? | Отвечают на вопросы, делают выводы. | Методы и приемы: словесный (беседа). Формы: фронтальная. | Регулятивные УУД: оценивать соответствие результата деятельности поставленной цели и условиям, объяснять причины достижения или недостижения цели, находить ошибку, давать оценку приобретённому опыту. Коммуникативные УУД: воспринимать и формулировать суждения в соответствии с условиями и целями общения; ясно, точно, грамотно выражать свою точку зрения. | Развивать умения сравнивать, обобщать, делать выводы.
| 7 мин |
Этап рефлексии учебной деятельности |
|
| Подвести итоги урока. Поставить оценки по трем пунктам: Активность в команде Командная работа Индивидуальная работа по маршрутному листу. Команды справившаяся первой выбирает сокровища первой, в коробке бриллианты с оценкой 5 по алгебре. Вторая команда получает монеты с оценкой 4 по алгебре. Третья команда получает утешительный приз. Рефлексию провести при помощи небольшой анкеты. (Приложение 4) Дать домашнее задание на выбор. | Ответить на вопросы рефлексии. | Методы и приемы: словесный (беседа). Формы: фронтальная, индивидуальная. | Регулятивные УУД: оценивать соответствие результата деятельности поставленной цели и условиям, объяснять причины достижения или недостижения цели, находить ошибку, давать оценку приобретённому опыту. Коммуникативные УУД: воспринимать и формулировать суждения в соответствии с условиями и целями общения; ясно, точно, грамотно выражать свою точку зрения. | Развивать у учащихся самостоятельность в мышлении и учебной деятельности.
| 4 мин |
| Вопросы | ДА | НЕТ | Вопросы | ДА | НЕТ |
| Я знаю определение квадратичной функции. |
|
| Я знаю определение квадратичной функции. |
|
|
| Я знаю, какая линия является графиком квадратичной функции. |
|
| Я знаю, какая линия является графиком квадратичной функции. |
|
|
| Я умею строить график квадратичной функции. |
|
| Я умею строить график квадратичной функции. |
|
|
| Я знаю свойства квадратичной функции. |
|
| Я знаю свойства квадратичной функции. |
|
|
| Я умею определять промежутки знакопостоянства. |
|
| Я умею определять промежутки знакопостоянства. |
|
|
| Я умею определять промежутки монотонности по графику квадратичной функции. |
|
| Я умею определять промежутки монотонности по графику квадратичной функции. |
|
|
| Я знаю как влияют коэффициенты а, с и дискриминант квадратного трехчлена на расположение графика квадратичной функции. |
|
| Я знаю как влияют коэффициенты а, с и дискриминант квадратного трехчлена на расположение графика квадратичной функции. |
|
|
| Я умею преобразовывать график квадратичной функции. |
|
| Я умею преобразовывать график квадратичной функции. |
|
|
| Я умею определять значения аргумента и значение функции. |
|
| Я умею определять значения аргумента и значение функции. |
|
|
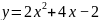
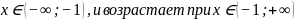
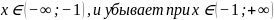
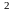 +2х +8
+2х +8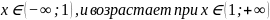
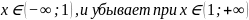
 )
)