8.1.1.2 санның квадрат түбірі және арифметикалық квадрат түбірі ұғымдарын біледі және ажыратады;
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Квадрат түбірлер
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Квадрат түбірлер»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1990 руб.
3320 руб.
1990 руб.
3320 руб.
1800 руб.
3000 руб.
1990 руб.
3310 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
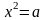 , мұндағы
, мұндағы 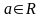 түріндегі теңдеулерді шешеді.
түріндегі теңдеулерді шешеді.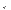 » символы туралы қысқаша тарихи ақпарат енгізілген.
» символы туралы қысқаша тарихи ақпарат енгізілген. 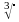 » математикалық символы көрсетіледі.
» математикалық символы көрсетіледі.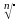 » математикалық символы арқылы жазылады.
» математикалық символы арқылы жазылады.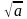 жазылымы «a санының квадрат түбірі» деп оқылатынын мұғалім көрсетеді («арифметикалық» сөзі айтылмайды).
жазылымы «a санының квадрат түбірі» деп оқылатынын мұғалім көрсетеді («арифметикалық» сөзі айтылмайды).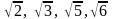 және т.б. сандары сияқты.
және т.б. сандары сияқты.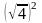 ,
, 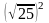 ,
, 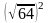 . Алғашқы екі мысалды шығарғаннан кейін мұғалім оқушыларға келесі сұрақты қояды: «Сіздер нені байқадыңыздар?». Осыдан кейін, байқалған заңдылықты формула түрінде жазып алып, осы формуланы үшінші мысалды шешуде қолдану ұсынылады. Осыдан кейін оқушылар сұраққа жауап береді «Бұл қасиет қандай жағдайларда дұрыс болады?» және өз жауаптарын негіздейді.
. Алғашқы екі мысалды шығарғаннан кейін мұғалім оқушыларға келесі сұрақты қояды: «Сіздер нені байқадыңыздар?». Осыдан кейін, байқалған заңдылықты формула түрінде жазып алып, осы формуланы үшінші мысалды шешуде қолдану ұсынылады. Осыдан кейін оқушылар сұраққа жауап береді «Бұл қасиет қандай жағдайларда дұрыс болады?» және өз жауаптарын негіздейді. 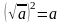 және арифметикалық квадрат түбір анықтамасынан, егер
және арифметикалық квадрат түбір анықтамасынан, егер  және
және 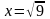 бен
бен 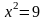 теңдеулерінің нақты сандар жиынында қандай мағынасы болатынын анықтау.
теңдеулерінің нақты сандар жиынында қандай мағынасы болатынын анықтау. 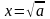 мен
мен 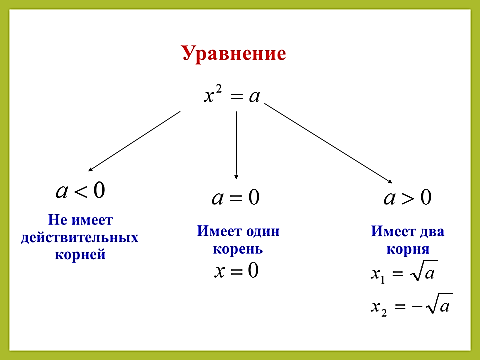
 болатынына аударады, ал егер
болатынына аударады, ал егер 















