Использование проблемных ситуаций на уроках математики
Согласно высказываниям американского философа, психолога и педагога Джона Дьюи (1859-1952), мыслить человек начинает тогда, когда сталкивается с трудностями, преодоление которых имеет для него большое значение. Впоследствии, за «трудностями», которые нужно преодолеть, размышляя над поиском решения, закрепилось название «проблема».
Учитель осуществляет проблемное обучение, если не даёт информацию в готовом виде, а организовывает работу так, что ребята сами открывают новое знания. От учителя требуется лишь правильное использование всех тех ресурсов, которые скрыты в курсе преподаваемого предмета.
На основании обобщения собственного опыта с учетом передового педагогического опыта1 (под передовым педагогическим опытом понимают опыт, позволяющий получить наиболее высокие и качественно новые результаты) можно указать несколько основных приёмов создания проблемных ситуаций:
учитель подводит школьников к противоречию и предлагает им самим найти способ его разрешения;
излагает различные точки зрения на один и тот же вопрос;
сталкивает противоречия практической деятельности;
предлагает классу рассмотреть явление с различных позиций;
побуждает учащихся делать сравнения, обобщения, выводы из ситуации, сопоставлять факты;
ставит конкретные вопросы (на обобщение, обоснования, конкретизацию, логику рассуждения;
определяет проблемные теоретические и практические задания;
ставит проблемные задачи (с недостаточными или избыточными исходными данными; с неопределенностью в постановке вопроса; с противоречивыми данными; с заведомо допущенными ошибками; с ограниченным временем решения; на преодоление психической инерции и другим);
предлагает составить задачи самостоятельно.
Покажу эти приёмы на конкретных заданиях.
Учитель подводит школьников к проблеме и предлагает им самим найти способ её разрешения.
Побуждение к осознанию противоречия осуществляется вопросами учителя: «Что вас удивило? Что интересного заметили? Какое противоречие налицо?».
Тема: «Прямая. Луч. Отрезок»
а) Проведи прямую линию так, чтобы она пересекала кривую линию:
в двух точках; в трех точках; в пяти точках; в шести точках;
б) Проведи луч так, чтобы он пересекал кривую линию:
в двух точках; в трех точках; в пяти точках; в шести точках;
в) Проведи отрезок так, чтобы он пересекал кривую линию:
в двух точках; в трех точках; в пяти точках; в шести точках;

Тема: «Простые и составные числа»
Прочитай “лишнее” число: 2, 3, 5, 7, 9, 11,13,17.
Сталкивает противоречия практической деятельности
Побуждение к осознанию противоречия осуществляется репликами: «Вы смогли выполнить задание? В чем затруднение? «Почему так получилось? Чего мы еще не знаем?».
Тема: «Построение треугольника по трем элементам. Неравенство треугольника»
Построить с помощью циркуля и линейки треугольник со сторонами:
а) 5см; 6см; 7см;
б) 9см; 5см; 6см;
в) 1см; 2см; 3см;
г) 3см; 4см; 10см.
Тема: «Сумма внутренних углов треугольника»
Построить треугольник по трем заданным углам:
1)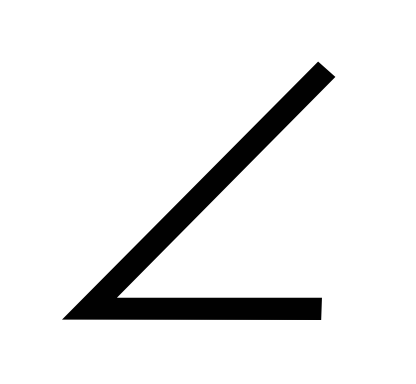 А=90°,
А=90°, 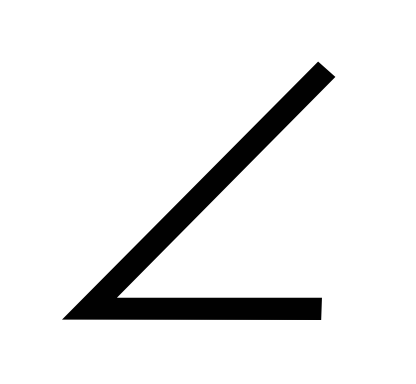 B=60°,
B=60°, 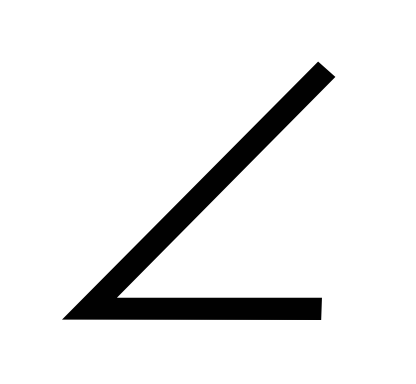 С=40°.
С=40°.
2) 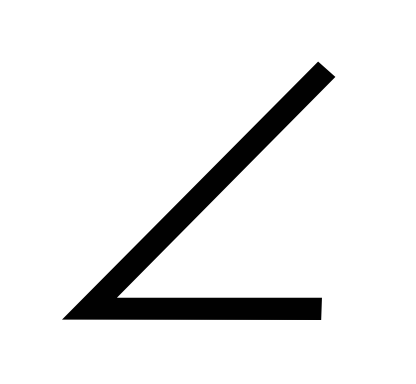 А=70°,
А=70°, 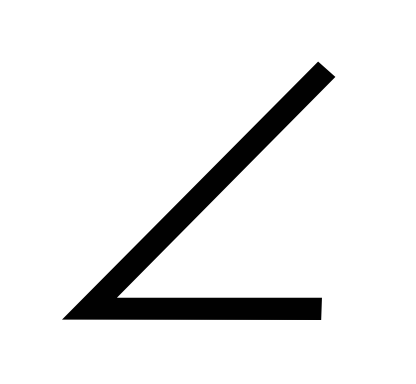 B=30°,
B=30°,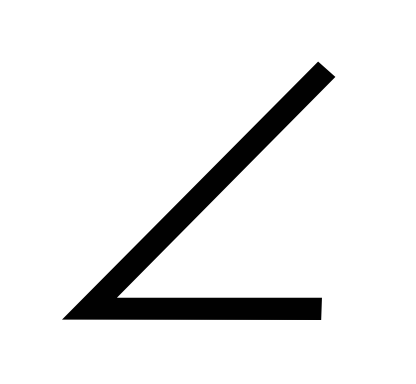 С=50°.
С=50°.
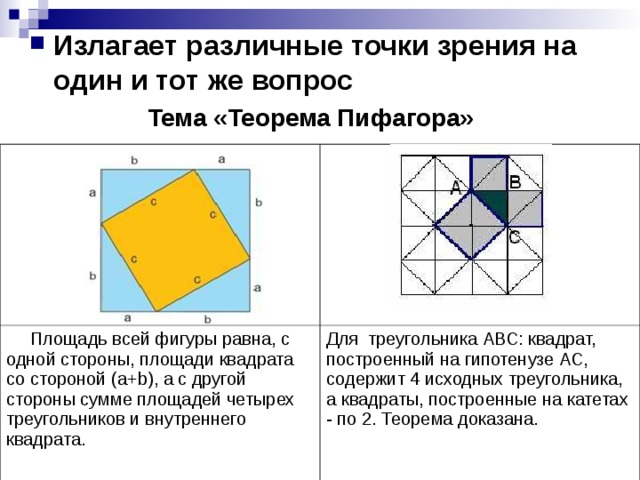
Излагает различные точки зрения на один и тот же вопрос
Тема «Теорема Пифагора»
| 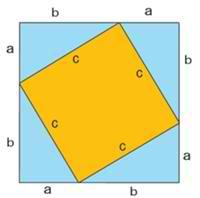
Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны сумме площадей четырех треугольников и внутреннего квадрата. 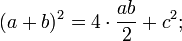 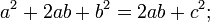 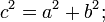 Что и требовалось доказать. | 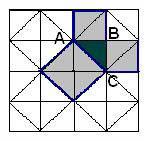
Для треугольника АВС: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах - по 2. Теорема доказана.
|
Ставит проблемные задачи (например, с недостаточными или избыточными исходными данными; с неопределенностью в постановке вопроса; с противоречивыми данными; с заведомо допущенными ошибками; с ограниченным временем решения), анализирует умение применять полученные знания
"Обманные задачи"
Постройте прямоугольник со сторонами 2; 3 и 5 см.
Больший угол треугольника равен 50°. Найдите остальные углы.
Диагональ ромба в два раза больше его стороны. Найдите углы ромба.
Найди ошибку:
| (-2)2 = -4 | -23 = -6 | (-5)2 = -25 | -32 = -9 | (-8)2 = 64 | -33 = -9 |
Задача с недостающими данными.
1.Банка с медом весит 500 г. Такая же банка с керосином - 350 г. Сколько весит пустая банка? (Нужно знать отношение веса меда и керосина.)
2. Даны две окружности, радиус одной из них - 3 см, расстояние между их центрами - 10 см. (Требуется знать радиус другой окружности.)
Тема «Формулы сокращённого умножения».
Учитель рассказывает: «Вчера по телевизору я смотрела передачу с участием экстрасенса, который произвёл на меня огромное впечатление. Я научилась быстро выполнять в уме операции над числами. Хотите я продемонстрирую свои способности?» Получив утвердительный ответ, учитель предлагает посоревноваться с ним в вычислениях.
І тур. Учитель просит кого – нибудь из ребят назвать два последовательных натуральных числа. Пусть школьник назовёт 129 и 130. Теперь учитель и класс вычисляют на скорость 1302 – 1292. Победителем, причём мгновенно, выходит учитель.
ІІ тур. Вновь учитель обращается к одному из учеников и просит того назвать любые два числа. Пусть ученик назвал 1,43 и 2,51. Теперь класс и учитель соревнуются при вычислении значения выражения:
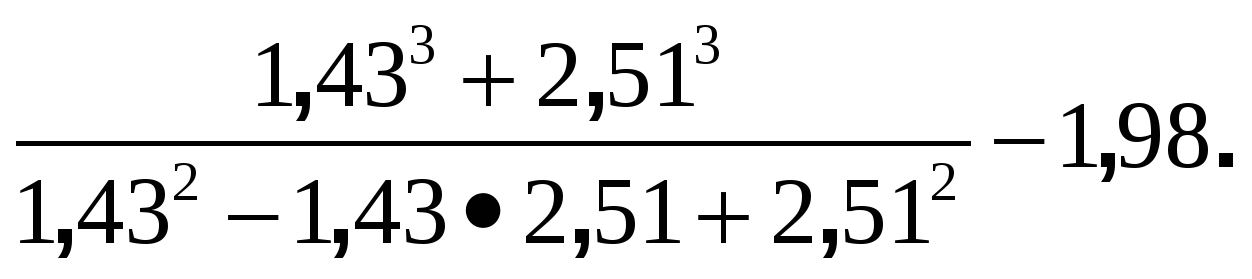
Понятно, что учитель, пользуясь формулами сокращённого умножения, легко побеждает в соревновании. Изменяя задания, неизменно побеждая, учитель, в конце концов, добьётся от ребят фразы типа: «Вы что-то знаете!»
«Да, я действительно что-то знаю,- заявляет учитель. – Вы также узнаете это что-то на сегодняшнем уроке и сможете быстро выполнять такие вычисления».
Заключение.
Организация проблемного обучения действительно способствует развитию умственных сил учащихся (противоречия заставляют задуматься, искать выход из проблемной ситуации, ситуации затруднения), самостоятельности (самостоятельное видение проблемы, формулировка проблемного вопроса, проблемной ситуации, самостоятельность выбора плана решения), развитию творческого мышления (самостоятельное применение знаний, способов действий, поиск нестандартного решения). Следовательно, оно обеспечивает особый тип мышления, глубину убеждений, прочность усвоения знаний и творческое их применение в практической деятельности.
Но существуют и слабые стороны проблемного обучения:
значительно большие расходы времени на изучение учебного материала;
малая эффективность их при усвоении принципиально новых разделов учебного материала, где не может быть применен принцип опоры на прежний опыт;
в меньшей мере применимо при изучении сложных тем, где крайне необходимо объяснение учителем, а самостоятельный поиск оказывается недоступным для большинства школьников.
Вечно изобретать, пробовать, совершенствовать и совершенствоваться - вот единственный курс учительской жизни...
К.Д.Ушинский
5