Золотое сечение

Разработка от крытого урока «Золотое сечение»

ЗОЛОТОЕ СЕЧЕНИЕ

…Геометрия владеет двумя

сокровищами – теоремой

Пифагора и золотым сечением, и

если первое из них можно

сравнить с мерой золота, то

второе - с драгоценным

камнем…

Иоганн Кеплер

Содержание:

«золотое сечение», «золотой треугольник», «золотой прямоугольник», «золотая спираль»; числовое значение золотого отношения; деление отрезка в золотом отношении.

Цели изучения:

1. расширить кругозор учащихся, способствовать развитию познавательного интереса

2. показать школьникам общеинтеллектуальное значение математики

3. способствовать познанию законов красоты и гармонии окружающего мира.

Прогнозируемый результат:

1. знать понятия «золотое сечение», «золотой

треугольник»,»золотой прямоугольник».

2. знать числовое значение золотого соотношения

3. уметь делить отрезок в золотом соотношении.

Оборудование:

Чертежные инструменты, мультимедиа

Ход урока:

Окружающий нас мир многообразен.

Вы, наверное, обращали внимание на то, что мы неодинаково относимся к предметам и явлениям окружающей действительности. Беспорядочность, бесформенность несоразмерность воспринимается нами как нечто безобразное и производят отталкивающее впечатление. А предметы и явления, которым свойственна мера, целесообразность и гармония воспринимаются как красивые и вызывают у нас чувство восхищения, радости и поднимают настроение…

Людей с давних времен волновал вопрос: подчиняются ли такие неуловимые вещи, как красота и гармония математическим расчетам…? Это будет основной вопрос, ответ на который мы должны будем получить в конце нашего урока.

Сегодня на уроке мы познакомимся с одним из математических соотношений, в котором присутствует красота. А ваша задача состоит в том, чтобы приняв активное участие на уроке, сделать для себя вывод относительно поставленного вопроса.

Итак, тема нашего сегодняшнего урока – «Золотое сечение как гармония форм природы и искусства». Откройте свои тетради, запишите число и тему урока.

Эпиграфом к нашему уроку будут слова немецкого астронома и математика – исследователя Иоганна Кеплера (слайд №2)

Теорему Пифагора знают почти все… а «золотое сечение далеко не все» Сегодня мы познакомимся с этим понятием. Мы увидим где оно встречается в природе.

Что же такое золотое сечение? Это есть деление отрезка в определенном отношении, а в каком именно сейчас рассмотрим. Как правило способов деление отрезка АВ точкой С бесчисленно много… однако, говорят, что точка С производит золотое сечение, если выполняется пропорция: длина меньшего отрезка относится к длине большего также как и длина большего отрезка относится к длине всего отрезка АВ. т.е. СВ:АС=АС:АВ.

Термин «золотое сечение» было введено в 16 веке ученым изобретателем, художником, Леонардо да Винчи. Золотое сечение также называли «божественным сечением», потому что оно вызывает ощущение красоты и гармонии. Но об этом чуть позже

Чтобы и вы могли увидеть золотое сечение в природе, в произведениях искусства, мы сейчас рассмотрим методику деления отрезка по золотому сечению…(слайд №3)

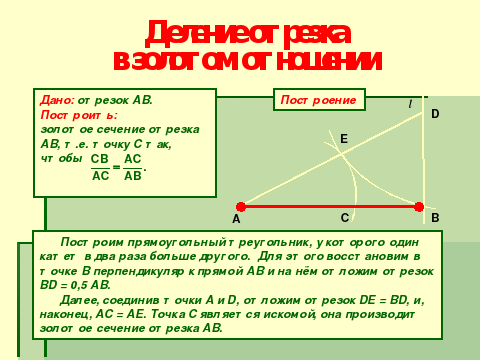
Рассмотрим конкретный пример, разделим отрезок АВ=4см по золотому сечению. ( ученики самостоятельно делят, один выполняет деление у доски)И найдем значение отношения. Что получилось? Интереееснооо… а давайте разделим отрезок АВ=9 см по золотому сечению … найдите значение отношения. Что получилось….. Оказывается какой бы отрезок мы не взяли, то отношение получаемое при золотом сечении практически не изменяется и всегда приблизительно равно 0,62… Такое отношение называют золотым.

Скажите, так в каком случае точка С производит золотое сечение?

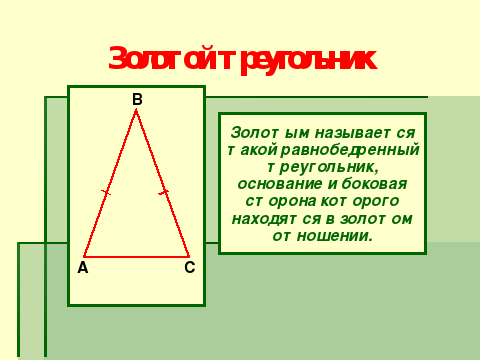
Оказывается существует так называемый золотой треугольник, золотой четырехугольник и золотая спираль. (слайд №4)

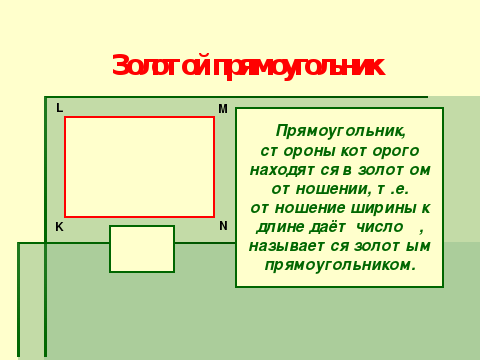
А сейчас проведем психологический опыт. Начертите прямоугольник, красивый, такой как вам понравится… и найдите отношение ширины к длине… (учитель проходит между рядами) что получилось? У большинства получилось число, близкое к значению золотого отношения. И это не случайно. Многим людям кажутся красивыми именно те фигуры, в которых есть элементы, связанные друг с другом золотым отношением. (слайд №5)

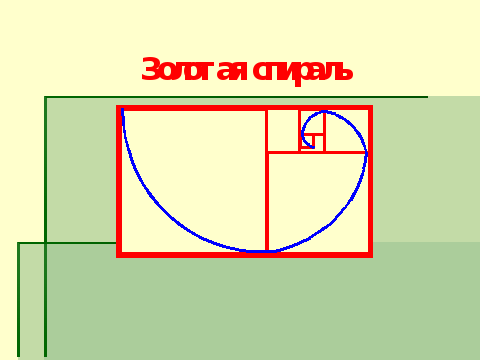
А теперь продолжим работу с золотым прямоугольником. В нем построим квадрат со стороной равной меньшей стороне прямоугольника, имеющий общий угол с золотым прямоугольником. . Оказывается мы снова получим золотой прямоугольник меньших размеров. Возьмем полученный золотой прямоугольник и проведем несколько аналогичных построений. ( Слайд 6)

Видим что весь прямоугольник оказался из вращающихся квадратов. Соеденим противолежащие вершины квадратов плавной кривой. Получаем кривую, которая золотой спиралью.

Где в природе встречается золотая спираль нам расскажет…….

(Доклад ученика)

« Здравствуйте, меня зовут….. я заметил(а) рассматривая расположение листьев на общем стебле многих растений , что между каждыми двумя парами листьев, третья расположена на месте золотого сечения.

Точка С делит отрезок АВ в золотом отношении итд.

Рассмотрим расположение семечек в корзине подсолнуха. Они выстраиваются вдоль спиралей, которые закручиваются как справа налево, так и слева направо. В одну сторону у среднего подсолнуха закручено 13 спиралей, а в другую – 21. Отношение 13:21 есть золотое отношение. В случае более крупного подсолнуха это отношение такое же. Похожее спиральное расположение чешуек сосновых шишек и ячеек ананаса.

По золотой спирали свернуты раковины многих улиток и моллюсков, некоторые пауки, сплетая паутину закручивают нити вокруг центра по золотым спиралям.

По золотым спиралям закручиваются многие галактики, в частности галактика Солнечной системы.

Из всего вышесказанного можно сказать, что золотое сечение - это один из основных основополагающих принципов природы. Спасибо » (доклад завершен»

Установлено, что золотое сечение можно найти и в пропорциях человека . Об этом нам расскажет ……(доклад ученика)

«Здравствуйте, меня зовут ….. я начну сразу с пропорции головы человека.

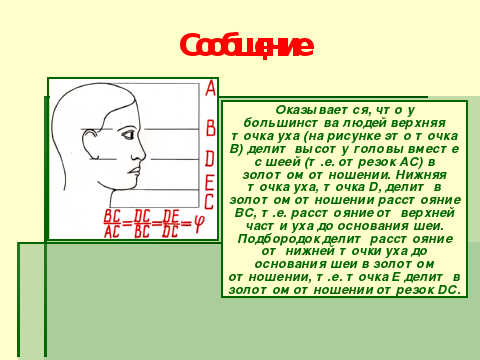
Перейду к пропорциям тела.

Спасибо» доклад завершен .

Проведем еще один психол.опыт. представьте, что вы собрались нарисовать пейзаж. Проведите линию горизонта. Найдите отношение высоты линии горизонта к высоте всей картины. Что получилось?

Итог урока:

ответьте на вопрос, который мы поставили в начале урока…( Людей с давних времен волновал вопрос: подчиняются ли такие неуловимые вещи, как красота и гармония математическим расчетам…?) Ответ?

Вам понятно значение золотого отношения в природе? В архитектуре итд? Надеюсь, теперь вы сможете увидеть золотую пропорцию в окружающем вас предметах. Спасибо…