Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Урок математики в 9 классе по теме: задачи на сложные проценты
Урок математики в 9 классе использовался в Витемлянской СОШ Погарского района с целью повторить и систематизировать знания в изучении задач на проценты
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Урок математики в 9 классе по теме: задачи на сложные проценты»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2100 руб.
3000 руб.
2000 руб.
2860 руб.
2000 руб.
2860 руб.
2220 руб.
3170 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
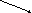
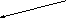
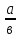 ·100%
·100% 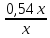 · 100% = 54% .
· 100% = 54% .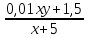 = 0,56
= 0,56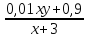 = 0,6
= 0,6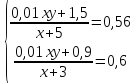
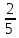 х
х 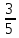 х
х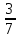 у
у 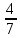 у
у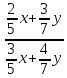 = 22
= 22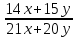 =
=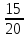 ,
, 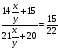 ,
, 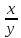 = t ,
= t , 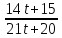 =
= 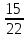
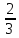 всей задолженности за первый год. Через два года долг фермера составил 64 % от первоначально взятой суммы. Сколько процентов берет банк за кредит на второй год.
всей задолженности за первый год. Через два года долг фермера составил 64 % от первоначально взятой суммы. Сколько процентов берет банк за кредит на второй год.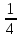 (х +0,01ху) (р)
(х +0,01ху) (р)
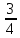 (х + 0,01ху) (р)
(х + 0,01ху) (р)