ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ДОПОЛНИТЕЛЬНОГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
(ПОВЫШЕНИЯ КВАЛИФИКАЦИИ)
«МОРДОВСКИЙ РЕСПУБЛИКАНСКИЙ ИНСТИТУТ ОБРАЗОВАНИЯ»
Курсовая работа
«ЭЛЕМЕНТЫ КОМБИНАТОРИКИ В КУРСЕ МАТЕМАТИКИ ОСНОВНОЙ ШКОЛЫ»
Выполнила: Самкина Т.Н..,
учитель математики
МБОУ «Поселковская СШ»
Атяшевского муниципального района Республики Мордовия
Руководитель: Куканов М.А.
САРАНСК 2015
СОДЕРЖАНИЕ:
ВВЕДЕНИЕ………………………………………………………………………..3
Общие сведения ……………………………………………………….…..5
Содержание вопроса комбинаторики и теории вероятностей в учебной литературе……………………………………………………………….….7
Анализ учебно-методической литературы по комбинаторике………….9
Заключение……………………………………………………………………….20
Список литературы………………………………………………………………21
ВВЕДЕНИЕ
«Число, место и комбинация – три взаимно перекрещивающиеся, но отличные сферы мышления, к которым можно отнести все математические идеи».
Дж. Сильвестр
Изучение вероятностно-статистического материала продиктовано самой жизнью. Современной России нужны люди, способные принимать нестандартные решения, умеющие творчески мыслить, хорошо ориентироваться в обычных житейских ситуациях и производственной деятельности. Вероятностный характер многих явлений действительности во многом определяет поведение человека, и курс должен формировать соответствующие практические ориентиры, вооружать учащихся, как общей вероятностной интуицией, так и конкретными способами оценки данных. Дети должны научиться извлекать, анализировать и обрабатывать разнообразную, порой противоречивую информацию, принимать обоснованные решения в ситуациях со случайными исходами, оценивать степень риска и шансы на успех. Необходимость формирования вероятностного мышления обусловлена и тем, что вероятностные закономерности универсальны: современная физика, химия, биология, демография, социология, лингвистика, весь комплекс социально-экономических наук развивается на базе вероятностно-статистической математики.
Вероятностно-статистический материал обладает огромным воспитывающим потенциалом, его изучение влияет на развитие интеллектуальных способностей, усиливает прикладной аспект курса математики, способствует развитию интереса к предмету.
Введение элементов статистики и теории вероятностей в содержание математического образования является одним из важнейших аспектов модернизации содержания образования, так как роль этих знаний в современном мире повышается.
Основными целями изучения курса являются следующие.
Способствовать формированию и развитию умений решения комбинаторных задач, позволяющих ученикам разумно организовать перебор ограниченного числа данных, подсчитать всевозможные комбинации элементов, составленных по определённому правилу.
Способствовать формированию и развитию вероятностного мышления, вероятностной интуиции.
Способствовать развитию творческих способностей и дарований.
Создать условия для развития умений самостоятельно приобретать и применять знания.
Создать условия для расцвета личности школьника с учётом его возрастных особенностей.
ОБЩИЕ СВЕДЕНИЯ
В обыденной жизни нам нередко встречаются задачи, которые имеют несколько различных вариантов решения. Чтобы сделать правильный выбор, важно не упустить ни один из них. Для этого надо уметь осуществлять перебор всех возможных вариантов или подсчитывать их число. Задачи, требующие такого решения, называются комбинаторными. Область математики, в которой изучают комбинаторные задачи, называется комбинаторикой.
Комбинаторика возникла в XVI веке и первоначально в ней рассматривались комбинаторные задачи, связанные в основном с азартными играми. В процессе изучения таких задач были выработаны некоторые общие подходы к их решению, получены формулы для подсчета числа различных комбинаций.
В настоящее время комбинаторика является одним из важных разделов математической науки. Ее методы широко используются для решения практических и теоретических задач. Установлены связи комбинаторики с другими разделами математики.
В начальном обучении математике роль комбинаторных задач постоянно возрастает, поскольку в них заложены большие возможности не только для развития мышления учащихся, но и для подготовки учащихся к решению проблем, возникающих в повседневной жизни.
Комбинаторные задачи в начальном курсе математики решаются, как правило, методом перебора. Для облегчения этого процесса нередко используются таблицы и графы. В связи с этим учителю необходимы определенные умения и навыки решения комбинаторных задач.
Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Комбинаторику можно рассматривать как введение в теорию вероятностей, поскольку методы комбинаторики используются для решения многих вероятностных задач, в которых речь идет о подсчете числа возможных исходов и числа благоприятных исходов в различных конкретных случаях.
Выбором объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности.
С аналогичными задачами, получившими название комбинаторных, люди сталкивались в глубокой древности. Уже несколько тысячелетий назад в Древнем Китае увлеклись составлением магических квадратов, в которых заданные числа располагались так, что их сумма по всем горизонталям, вертикалям и главным диагоналям была одной и той же. В Древней Греции подсчитывали число различных комбинаций длинных и коротких слов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей особым образом разрезанного квадрата и т.д.
Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д.
Комбинаторика становится наукой лишь в 18 веке - в период, когда возникла теория вероятностей. Чтобы решать теоретико-вероятностные задачи, нужно было уметь подсчитывать число различных комбинаций, подчиненных тем или иным условиям. После первых работ, выполненных в 18 веке итальянским ученым Дж. Кардано, Н. Тартальей, и Г. Галилеем, такие задачи изучали французские математики Б. Паскаль и П. Ферма. Первым рассматривал комбинаторику как самостоятельную ветвь науки немецкий философ и математик Г. Лейбниц, опубликовавший в 1666 году работу " Об искусстве комбинаторики", в которой впервые появляется сам термин "комбинаторный".
Замечательные достижения в области комбинаторики принадлежат Л.Эйлеру. Комбинаторными задачами интересовались и математики, занимавшиеся составлением и разгадыванием шифров, изучением древних письменностей. Теперь комбинаторика находит применение во всех областях науки и техники: в биологии, где она применяется для изучения состава белков и ДНК, в химии, в механике и т.д.
По мере развития комбинаторики выяснилось, что, несмотря на внешнее различие изучаемых ею вопросов, многие из них имеют одно и то же математическое содержание и сводятся к задачам о конечных множествах и их подмножествах. Постепенно выяснилось несколько основных типов задач, к которым сводится большинство комбинаторных проблем. Важную область комбинаторики составляет теория перечислений. С ее помощью можно пересчитать число решений различных комбинаторных задач.
СОДЕРЖАНИЕ ВОПРОСА КОМБИНАТОРИКИ И ТЕОРИИ ВЕРОЯТНОСТИ В УЧЕБНОЙ ЛИТЕРАТУРЕ
На рубеже третьего тысячелетия становится очевидной универсальность вероятностно-статистических законов, они стали основой описания научной картины мира. И ребенок в своей жизни ежедневно сталкивается с вероятностными ситуациями, ведь игра и азарт составляют существенную часть его жизни. Круг вопросов, связанных с осознанием соотношения понятий вероятности и достоверности, проблемой выбора наилучшего из нескольких вариантов решения, оценкой степени риска и шансов на успех, представлением о справедливости и несправедливости в играх и в реальных жизненных коллизиях – все это, несомненно, находится в сфере реальных интересов становления и развития личности.
Подготовку человека к таким проблемам и осуществляет школьный курс математики. Принципиальные решения о включении вероятностно-статистического материала как равноправной составляющей обязательного школьного математического образования приняты ныне и в нашей стране. Все перспективные государственные образовательные документы последних лет содержат вероятностно-статистическую линию в курсе математики 5-9 классов наравне с такими привычными линиями, как «Числа», «Функции», «Уравнения и неравенства», «Геометрические фигуры». Продолжение изучения этой линии предполагается в старших классах.
Современные стандарты и программы математического образования в основной школе предполагают пропедевтику основных понятий, знакомство на наглядном, интуитивном уровне с вероятностно-статистическими закономерностями в 5-6 классах, определение основных понятий, построение и изучение базовых вероятностно-статистических моделей – в 7-9 классах.
Первые учебники, в которых последовательно с 5 по 9 класс проводится вероятностно-статистическая линия, органично связанная с другими темами курса - это новый учебный комплект «Математика 5-6» по ред. Г.В. Дорофеева и И.Ф. Шарыгина, «Математика 7-9» под ред. Г.В. Дорофеева. в этих учебных комплектах принят статистический подход к понятию вероятности, который методически и психологически соответствует возрастным особенностям учеников основной школы.
Следует отметить, что наиболее подходит для реализации оптимального обучения школьников 10-11 лет математике учебный комплект под редакцией Г.В Дорофеева, а также комплект «Арифметика 5-6 класс» под редакцией С.М. Никольского. Был проведен сравнительный анализ обучения школьников 5-6 классов решению комбинаторных задач, обучающихся с помощью учебника С.М. Никольского и с помощью учебника Г.В. Дорофеева. Дети, наученные составлять дерево возможных вариантов, более осмысленно решали предложенные задачи, отсекая, если нужно, повторяющиеся комбинации. Так, решение задачи, с применением специальных методов, привело к правильному ответу на 37% учащихся больше, чем решение простым перебором.
Сохранение интереса к изучению математики при использовании новых комплектов учебников обеспечивается не только через дополнительные темы, но и через достаточное количество занимательных задач.
Занимательные задачи — инструмент для развития мышления, ведущего к формированию творческой деятельности школьника. К таким задачам относятся задачи «на соображение», «на догадку», головоломки, нестандартные задачи, логические задачи, творческие задачи. Например, задача 6-го класса: Восемь подружек решили обменяться фотографиями так, чтобы у каждой из них оказались фотографии остальных подруг. Сколько фотографий для этого потребуется.
Занимательный материал многообразен, но его объединяет следующее:
1. способ решения занимательных задач не известен;
2. занимательные задачи способствуют поддержанию интереса к предмету. Для решения занимательных задач характерен процесс поисковых проб. Появление догадки свидетельствует о развитии у детей таких качеств умственной деятельности как смекалка и сообразительность. Смекалка – это особый вид проявления творчества. Она выражается в результате анализа, сравнений, обобщений, установления связей, аналогий, выводов, умозаключений.
Систематизированный набор нестандартных задач применяется по индивидуальному плану учителя на уроках и во внеурочной работе. Конкретно можно рассмотреть некоторые темы: 5 класс, тема «Перебор возможных вариантов», в которой начинается изучение новой содержательной линии «Анализ данных»; 6 класс, тема «Вероятность события». Представлены характерные для комбинаторики задачи на размещения, сочетания, перестановки, но сами термины и формулы не рассматриваются. Предлагается более доступный детям данного возраста метод решения - построение дерева.
АНАЛИЗ УЧЕБНО-МЕТОДИЧЕСКОЙ ЛИНЕРАТУРЫ ПО КОМБИНАТОРИКЕ
В учебном пособии для проведения факультативного курса по теории вероятностей Лютикаса В.С. вначале даны сведения из прошлого теории вероятностей, затем достаточно подробно и систематично рассматриваются вопросы комбинаторики, вероятности события, операций над вероятностями, независимые повторные испытания (формулы Бернулли, Муавра-Лапласа, Пуассона и Лапласа), дискретные и непрерывные случайные величины, а также рассмотрены различные интересные задачи (например, задача Бюффона, парадокс Бертрана и т.д.). Эта книга интересна как с методической, так и с познавательной точек зрения. Она может быть одинаково доступна как учителю, так и ученику, так как написана простым, понятным языком, в ней дано много таблиц, диаграмм, все главы находятся во взаимосвязи. Материал систематичен и постепенно усложняется.
Книга предназначена для учителей, работающих в школах и классах с углублённым изучением математики. Она содержит методические рекомендации по изучению некоторых теоретических вопросов и решению задач, планирование уроков, образцы самостоятельных и контрольных работ по всем темам; эти материалы написаны в соответствии с учебным пособием Виленкина Н.Я., Ивашева-Мусатова О.С. и Шварцбурда С.И.
Книга посвящена элементарной комбинаторике, теории вероятностей и их приложениям, в ней систематически используется теоретико-множественный язык. Абстрактность этого языка компенсируется большим количеством подробно разобранных примеров. Задачи собраны в отдельные части, которые можно читать независимо. Там рассматриваются простые модели, связанные с приложениями комбинаторики и теории вероятностей. Книга предназначена для и преподавателей, учащихся, а также для студентов.
Авторы книги для внеклассного чтения Балк М.Б., Балк Г.Д. в интересном изложении дают комбинаторику и теорию вероятностей, кроме теории в этой книге есть исторические сведения, которые предлагается дать детям на занятиях кружков или факультативе по математике. После теории представлен набор занимательных задач на соединения без повторений и с повторениями. В отличие от пособия Лютикаса В.С. на занятия по теории вероятностей представлен материал только для одного или двух тематических занятий, а комбинаторика рассматривается без связи с теорией вероятностей. Но в книге представлен большой список литературы по комбинаторике и теории вероятностей.
Книга является пособием для факультетов подготовки учителей начальных классов. В ней дан достаточно большой объём материала по комбинаторике и, преимущественно, теории вероятностей. Этот материал отличается высоким уровнем сложности, он постепенно усложняется, в книге даны обширные исторические сведения.
В статье М.В. Ткачёвой под названием “Анализ данных в учебниках Н.Я. Виленкина и других” приводится пример того, как можно ввести в изучение математики V-IX классов новую содержательную линию, основная цель которой – формирование у учащихся элементарных статистических знаний, а также развитие комбинаторного и вероятностно-статистических стилей мышления. М.В. Ткачёва говорит о том, что вопросы статистики и комбинаторики можно вводить в изучение уже сейчас, на базе учебников и учебных пособий Виленкина Н.Я., Жохова В.И., Чеснокова А.С., Шварцбурда С.И. и др. “Математика 5” и “Математика 6” (М.: Мнемозина, 1996 и далее), которые сейчас наиболее распространены в школах России. Так, предлагается в практически каждой теме решать с детьми комбинаторные задачи при изучении натуральных чисел, операциях над ними, обыкновенных, десятичных дробей, операций над десятичными дробями (5 кл.); при изучении делимости чисел, умножение и деление натуральных и отрицательных чисел, при решении уравнений (6 кл.), далее эта линия усложняется введением элементов статистики и теории вероятностей (систематизация и подсчёт данных в частотных таблицах, столбчатые диаграммы, среднее значение и мода как характеристики совокупности числовых данных (5 кл.); нахождение частот данных по их относительным частотам в выборке заданного объёма и обратно, систематизация и представление данных в частотных таблицах, представление распределения данных в выборке в виде полигона частот (6 кл.). В статье приведён вариант планирования (для 5-6 классов), даны способы адаптации материала учебника к введению элементарных комбинаторных и статистических знаний. Т.е. комбинаторный материал даётся применительно к темам, изучаемым в нынешнем школьном курсе математики. Элементы теории вероятностей вводятся на практических занятиях (например, практическая работа по сбору, распределению данных по признакам, представление их в виде частотных таблиц) и в задачах.
Также в журнале “Математика в школе” есть статья от министерства образования, в которой говорится о том, что одним из важнейших аспектов модернизации содержания математического образования состоит во включении в программы элементов статистики и теории вероятностей. Изучение элементов комбинаторики, статистики и теории вероятностей в основной и старшей школе станет обязательным после утверждения федерального компонента государственного стандарта общего образования. Но в связи с тем, что внедрение в практику этого нового материала требует несколько лет и накопления методического опыта, Министерство образования РФ рекомендовало образовательным учреждениям начинать его преподавание в основной школе уже в 2003-2004 учебном году перечислен примерный круг вопросов, на которые следует ориентироваться учителям при введении комбинаторики, статистики и теории вероятностей в основной и старшей школе. Причем рекомендуется начинать изучение этих вопросов уже в 5 классе, т.к., по мнению психологов, дети этого возраста способны усвоить комбинаторный и статистический материал наиболее продуктивно. Кроме этого, в статье приведён достаточно большой список литературы по данной теме (включая учебники, вкладыши к ним, дополнительную литературу по данной теме и материалы для организации подготовки учителей).
В 2003 году издательство «Просвещение» опубликовало учебное пособие Макарычев Ю.Н., Миндюк Н.Г. «Элементы статистики и теории вероятностей» (под редакцией С.А. Теляковского). Книга предназначена для учащихся VII-IX классов и дополняет учебно-методический комплект: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. «Алгебра 7», «Алгебра 8», «Алгебра 9» (под редакцией С.А. Теляковского), который сегодня является самым массовым, наиболее широко используемым учебным пособием по математике в основной школе. Поэтому выход в свет дополнения к указанному комплекту, предназначенного для изучения вероятностно-статистического материала, свидетельствует о том, что введение новой вероятностно-статистической линии в школьное математическое образование уже стало реальностью и данное пособие является основным для изучения этой линии.
Учебное пособие «Элементы статистики и теории вероятностей» содержит теоретический и практический материал по элементам статистики и теории вероятностей, а также методический комментарий и планирование, составленное из расчета, что на изучении математики в VII-IX классах отводится 5 часов в неделю.
Небольшое по объему пособие состоит из четырех параграфов и дополняет учебники:
1. Статистические характеристики.
2. Статистические исследования.
3. Элементы комбинаторики.
4. Начальные сведения из теории вероятностей.
Структура пособия аналогична структуре указанных выше учебников. Параграфы делятся на пункты. В каждом пункте содержатся теоретические сведения и соответствующие упражнения. В конце пункта приводятся упражнения для повторения. К каждому параграфу даются дополнительные упражнения более высокого уровня сложности по сравнению с основными упражнениями.
Концепция введения элементов статистики и теория вероятностей в основной школе, которой придерживаются авторы нового пособия, в основном совпадает с концепцией, реализованной в рамках учебного комплекта «Математика 7», «Математика 8», «Математика 9» под редакцией Г.В.Дорофеева, но материал несколько сокращен. Исключением является только параграф об элементах комбинаторики. Он помещен в курс IX класса (а не в VII класс, как это сделано в УМК под ред. Г.В.Дорофеева) и содержит гораздо больше и теоретических сведений и практических упражнений, чем соответствующий материал в учебнике «Математика 7» под ред. Г.В.Дорофеева.
Остановимся подробнее на особенностях предлагаемых подходов к изучению элементов статистики в курсе алгебры 7-8 классов.
В VII классе учащиеся знакомятся с такими простейшими статистическими характеристиками, как среднее арифметическое, мода, медиана, размах. Их содержательный смысл разъясняется на примерах. Учащиеся должны знать соответствующие определения, научиться находить эти характеристики в несложных случаях, понимать их практический смысл в конкретных ситуациях. На изучение этого материала рекомендуется выделить 4 урока в конце учебного года за счет времени, отводимого на итоговое повторение.
Среднее арифметическое ряда данных является одним из основных статистических показателей. Оно используется в статистике наряду с такими средними величинами, как средняя квадратичная, средняя гармоническая.
Авторы подробно рассматривают графические способы представления статистических данных. При этом предлагают использовать столбчатую диаграмму для изображения распределения частот дискретных данных.
Наибольший объем материала запланирован для изучения в IX классе. Этот материал объединен в два параграфа: «Элементы комбинаторики» и «Начальные сведения из теории вероятностей», причем второй параграф включает два пункта, один из которых – обязательный, а решение об изучении второго пункта принимает учитель. На изучение вероятностно-статистического материала в IX классе выделяется 12 уроков (или, по решению учителя, 15 уроков), из них 8 уроков – на комбинаторику, 3 урока (или, по решению учителя, 6 уроков) – на теорию вероятностей и 1 урок – контрольная работа.
Элементы комбинаторики излагаются традиционно. Сначала на простых примерах демонстрируется решение комбинаторных задач методом перебора возможных вариантов. Затем разъясняется и формулируется комбинаторное правило умножения (которое чаще называют правилом произведения).
Далее последовательно вводятся понятия перестановки, размещения из n элементов по k и сочетания из n элементов по k. С помощью комбинаторного правила умножения выводятся формулы для вычисления числа всевозможных перестановок, размещений и сочетаний из данного числа п элементов. Изложение материала сопровождается большим числом задач для самостоятельного решения. Комбинации с повторением элементов не рассматриваются (кроме нескольких несложных примеров).
Соответствующее планирование приведено в «Методическом комментарии» в конце указанного пособия.
В §3 «Элементы комбинаторики» содержится четыре пункта:
1. Примеры комбинаторных задач.
2. Перестановки.
3. Размещения.
4. Сочетания.
Последний параграф пособия «Начальные сведения из теории вероятностей» включает в себя два пункта:
Вероятность случайного события.
Сложение и умножение вероятностей.
Как указывают авторы в методическом комментарии к пособию, в пункте «Вероятность случайного события» вводятся начальные понятия теории вероятностей, формируется представление о случайных, достоверных и невозможных событиях, приведены статистическое и классическое определение вероятности. При вычислении вероятностей используются формулы комбинаторики.
Авторы пособия использовали тот же подход к введению базовых понятий теории вероятностей, который реализован в УМК под редакцией Г.В. Дорофеева: школьникам показывают, что понимать под словом «вероятность» и как оценивать вероятность наступления несложных случайных событий сначала на качественном уровне – по результатам простейших экспериментов, а позднее происходит количественный подсчет вероятностей. Однако, при реализации этого подхода авторы пособия, будучи жестко ограниченными выделенным на изучение временем и, как следствие, малым объемом пособия, проявили определенную непоследовательность – не смогли избежать некоторых противоречий и не дали четкого понятия о вероятности случайного события и способах ее нахождения в различных частных случаях. Пункт «Вероятность случайного события» начинается с рассмотрения эксперимента и его результата.
В последнем пункте пособия «Сложение и умножение вероятностей» рассматриваются теоремы сложения и умножения вероятностей и связанные с ними понятиями. Авторы вводят понятие несовместных событий и рассматривают случаи наступления одного из двух несовместных событий, не вводя понятия «сумма случайных событий». Далее разъясняется понятие «противоположные события» и формулируется утверждение о сумме вероятностей противоположных событий.
В заключении авторы формулируют утверждение о вероятности события, состоящего в совместном появлении двух независимых событий. При этом не вводится понятие «произведение случайных событий», не вводится и понятие условной вероятности.
В заключении отметим, что пособие содержит большое количество интересных, хорошо подобранных упражнений разного уровня сложности, к большинству из которых даны ответы и указания по решению. К сожалению, в ответах много опечаток, есть неточности и ошибки (подробное рассмотрение ошибок имеется в статье В.Н. Студенецкой, О.М. Фадеевой «Статистика и теория вероятностей на пороге основной школы»).
Материал пункта 1 является подготовительным к пунктам 2-4. в нем рассматриваются примеры комбинаторных задач, при решении которых требуется непосредственно составлять те или иные комбинации и лишь после этого подсчитывать число возможных вариантов. Этот этап очень важный. В процессе составления различных комбинаций учащиеся начинают понимать структуру той или иной комбинации, а также усваивают способы рассуждений и подсчета вариантов. Здесь же разъясняется и формулируется комбинаторно правило умножения, которое неоднократно используется при изучении последующего материала.
Для того чтобы разъяснить учащимся смысл этого правила, рассматривается такая задача: «Сколько трехзначных чисел можно составить из цифр 1, 3, 5, 7, используя в записи числа каждую из них не более одного раза?».
При решении этой задачи сначала составляется древо всех возможных вариантов.
| Первая цифра | 1   | 3   | 5   | 7   |
| Вторая цифра |
3 |
5 |
7 |
1 |
5 |
7 |
1 |
3 |
7 |
1 |
3 |
5 |
| Третья цифра | 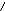
5 | 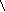
7 | 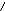
3 | 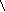
7 | 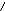
3 | 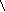
5 | 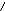
5 | 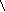
7 | 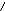
1 | 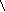
7 | 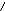
1 | 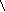
5 | 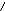
3 | 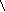
7 | 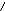
1 | 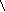
7 | 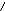
1 | 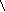
3 | 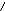
3 | 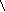
5 | 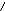
1 | 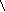
5 | 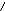
1 | 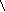
3 |
Далее делается важное замечание, что ответ на поставленный вопрос в задаче можно получить, не выписывая сами числа и не строя дерево возможных вариантов. Рассуждать будем так. Первую цифру трехзначного числа можно выбрать четырьмя способами. Так после выбора первой цифры останутся три, то вторую цифру можно выбрать из оставшихся цифр уже тремя способами. Наконец, третью цифру можно выбрать (из оставшихся двух) двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 4·3·2 = 24.
После этого формулируется комбинаторное правило умножения: «Пусть имеется n элементов и требуется выбрать один за другим некоторые k элементов. Если первый элемент можно выбрать n1 способами, после чего второй элемент можно выбрать из оставшихся n2 способами, затем третий элемент – n3 способами и т.д., то число способов, которыми могут быть выбраны все k элементов, равно произведению n1·n2·n3·…·nk».
Применение правила умножения иллюстрируется на следующем примере:
«Из города А в город В ведут две дороги, из города В в город С – три дороги, из города С до пристани – две дороги (рис. 1). Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?
Решение. Путь из А в В туристы могут выбрать двумя способами. Далее в каждом случае они могут проехать из В в С тремя способами. Значит, имеется 2·3 вариантов маршрута из А в С. Так как из города С на пристань можно попасть двумя способами, то всего существует 2·3·2, т.е. 12 способов выбора туристами маршрута из города А к пристани.
Упражнения в данном пункте направлены на составление различных комбинаций и подсчет числа возможных вариантов этих комбинаций.
В конце пункта 4 помещены задания смешанного типа, в которых рассматриваются различные комбинации элементов (перестановки, размещения, сочетания).
Дополнительные упражнения к §3 «Элементы комбинаторики» включают усложненные задания. Они могут быть использованы в работе с учащимися, проявляющими интерес и склонности к математике.
В 2004 году издательством «Дрофа» было выпущено пособие Е.А. Бунимовича, В.А. Булычева «Основы статистики и вероятность» для 5-9 классов. Пособие содержит необходимый теоретический и интересный практический материал для изучения новой вероятностно-статистической линии. Пособие может быть использовано вместе с любым из действующих учебников.
Цель данного пособия – помочь ребенку в формировании вероятностного мышления, в освоении школьного курса «Вероятность и статистика», помочь учителю в постановке преподавания этого нового материала.
В книге содержится дополнительный теоретический материал и соответствующие ему блоки задач, которые могут оказаться полезными для проведения занятий в профильных классах, математических кружках и на факультативах. Ко всем задачам учебного пособия даны ответы, а к большинству задач – подробные указания, комментарии и решения.
Заключение
В данной курсовой работе была сделана попытка проанализировать возможность реализации комбинаторики в основной школе. Была проанализирована различная учебно-методическая литература по этой теме и на основе этого анализа сделаны конкретные выводы, с краткими методическими рекомендациями.
На основе этих выводов разработана методика реализации комбинаторики в основной школе по каждому классу, в каждом из которых рассматривается ведение всех направлений.
Данная методическая разработка лишь один из вариантов реализации комбинаторикив курсе основной школы. По данной теме сейчас активно ведется работа по всем направлениям, так как на данный момент осталось еще немало нерешенных проблем связанных с реализацией этой линии в основной школе.
Список литературы
Бунимович Е.А., Булычев В.А. Вероятность и статистика. Пособие для общеобразовательных учебных заведений. – М.: Дрофа, 2002.
Бунимович Е.А., Булычев В.А. Основы статистики и вероятность. 5-9 кл.: Пособие для общеобразовательных учреждений – М.: Дрофа, 2004.
Дорофеев Г.В. Петерсон А.Г. Математика. 5-й класс. Часть 1: Учеб. для общеобразоват. учеб.заведений. – М.: издательство «Ювента», 2002.
Дорофеев Г.В. Петерсон А.Г. Математика. 5-й класс. Часть 2: Учеб. для общеобразоват. учеб.заведений. – М.: издательство «Ювента», 2002.
Дорофеев Г.В. Петерсон А.Г. Математика. 6-й класс. Часть 1: Учеб. для общеобразоват. учеб.заведений. – М.: издательство «Ювента», 2002.
Дорофеев Г.В. Петерсон А.Г. Математика. 6-й класс. Часть 2: Учеб. для общеобразоват. учеб.заведений. – М.: издательство «Ювента», 2002.
Дорофеев Г.В. Петерсон А.Г. Математика. 6-й класс. Часть 3: Учеб. для общеобразоват. учеб.заведений. – М.: издательство «Ювента», 2002.
Дорофеев Г.В., Суворова С.Б., Шарыгин И.Ф. и др. Математика. 6-й класс: Учеб. для общеобразоват. учеб.заведений - М.: Дрофа, 1997.
Дорофеев Г.В.Математика. 6-й класс: Рабочая тетрадь: К учебнику под редакцией Г.В.Дорофеева, И.Ф.Шарыгина "Математика 6". - М.: Дрофа, 1998.
Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Элементы статистики и теории вероятностей. Учебное пособие для учащихся 7-9 классов общеобразовательных учреждений/ под редакцией Теляковского С.А. – М., «Просвещение», 2003.
Тюрин Ю.Н., Макаров А.А., Высоцкий И.Р., Ященко И.В. Теория вероятностей и статистика. – М.: МЦНМО: АО «Московские учебники», 2004.
Тюрин Ю.Н., Макаров А.А., Высоцкий И.Р., Ященко И.В. Теория вероятностей и статистика. – 2-е изд., переработанное. – М.: МЦНМО: АО «Московские учебники», 2008.
Фадеев Д.К., Никулин М.С., Соколовский И.Ф. Элементы высшей математики для школьников. - М.: Наука, главная редакция физико-математической литературы, 1987.
Журнал «Математика в школе» №9, 2001
Журнал «Математика в школе» №5, 2003
Журнал «Математика в школе» №6, 2003
Журнал «Математика в школе» №5, 2004
Журнал «Математика в школе» №6, 2004
23