Учитель: Изучение нового материала мы начнем с понятия неравенства второй степени.
Задание 1. Какие из неравенств вы бы назвали неравенствами второй степени:
1) 6х2 – 13х>0; 2) x2 – 3x – 14>0; 3) (5 + x)(x – 4)>7;
4) ; 5) ; 6) ;
7) 8x2>0; 8) (x – 5)2 – 25>0; 9) x(x – 9) – x2>0?
– Теперь давайте сформулируем определение неравенства второй степени:
Определение: Неравенство, левая часть которого есть многочлен второй степени, а правая – нуль, называется неравенством второй степени.
Все квадратные неравенства могут быть приведены к одному из следующих видов:
1) ах2 + bx + c > 0;
2) ах2 + bx + c < 0;
3) ах2 + bx + c > 0;
4) ах2 + bx + c < 0.
Задание 2. Какие из чисел являются решениями неравенства ?
1
– 3
0
– 1
5
– 4
– 2
0,5
– К квадратным неравенствам нас приводят следующие задачи.
Задание 3. Планируется разбить прямоугольный цветник, который будет примыкать к дому. Заготовленного штакетника хватит на изгородь длиной 20м. Какими должны быть длина и ширина цветника, чтобы он имел площадь не менее: 1) 48 м2; 2) 50 м2.
– Обсудим выполнение этого задания.
Если за х м принять длину стороны цветника, примыкающей к дому, то решение задачи сведется к решению неравенств:
1) (20 – 2х)х > 48;
2) (20 – 2х)х > 50.
Используя преобразования, эти неравенства можно привести к таким неравенствам второй степени:
1) х2 – 10х + 24 < 0; 2) х2 – 10х + 25 < 0.
Попробуем найти способ решения квадратных неравенств, использующий свойства квадратичной функции.
Учащиеся пытаются предложить такой способ. Если идей не возникает, то учитель предлагает выполнить еще одно задание.
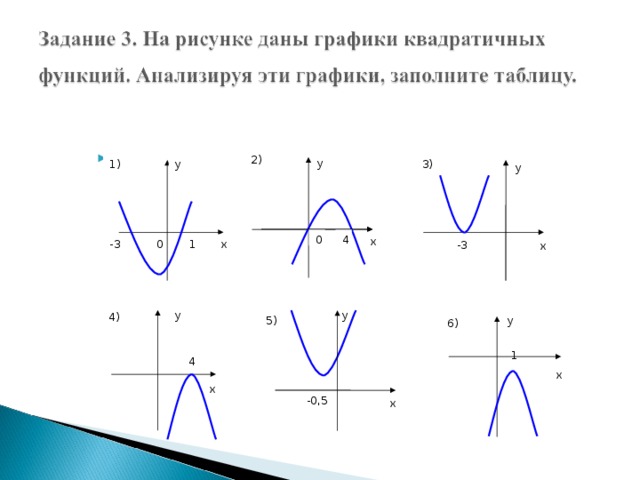
Задание 3. На рис. 1 даны графики квадратичных функций. Анализируя эти графики, заполните таблицу. (ПРИЛОЖЕНИЕ 2)
Рис. 1
Учитель: Теперь нам предстоит решить неравенство – х2 + 8x – 12 > 0.Какая информация о квадратичной функции может оказаться при этом полезной:
1.знак коэффициента а; направление ветвей параболы;
2.знак дискриминанта D квадратного трехчлена;
3.пересечение параболы с осями координат;
4.координаты вершины параболы;
5.примерное расположение параболы?
Обязательно ли для решения неравенства строить график соответствующий квадратичной функции? Если да, то с какой точностью выполнять построение?
Далее рассматриваются различные варианты неравенств с подробным решением и записью в тетради (или справочники).(ПРИЛОЖЕНИЕ 1) (слайды 7-13)
Задания:
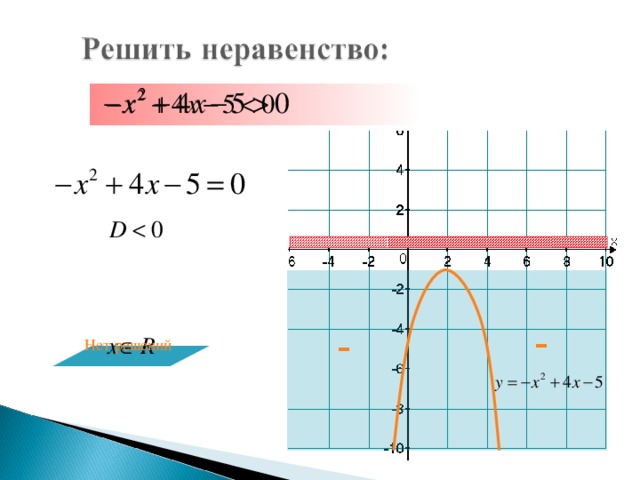
1) – х2 + 8х – 12 > 0.
Решение: Пусть у = – х2 + 8х – 12.
а = – 1, а<0. Ветви параболы направлены вниз.
– х2 + 8х – 12 = 0; D = 82 – 4(– 1)(– 12) = 16 = 42, D > 0
x1 = 6; x2 = 2.
Схематически строим график функции.
Ответ: х (2; 6).
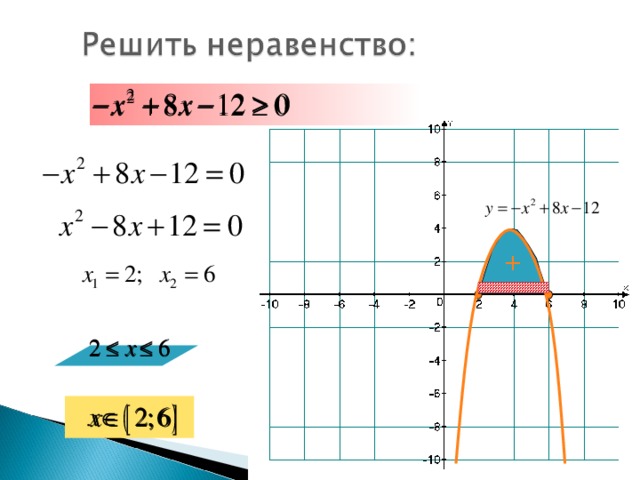
2) – х2 + 8х – 12 ≥ 0. Ответ: [2;6].
3) – х2 + 8х – 12 < 0. Ответ: (– ; 2) (6; + ).
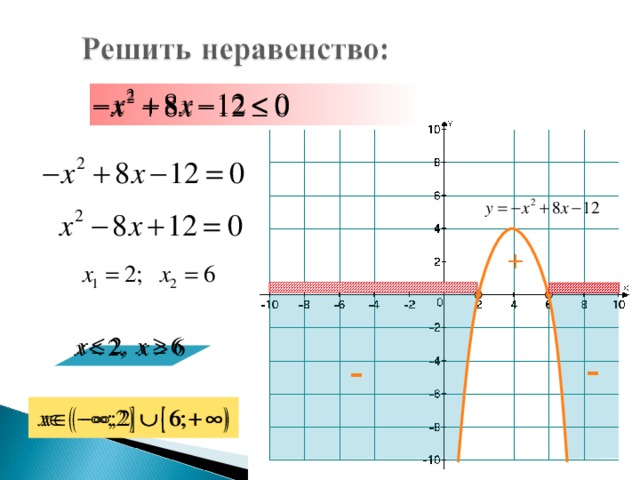
4) – х2 + 8х – 12≤0. Ответ: (– ; 2] [6; + ).
5) x2 – 8x + 12 > 0. Ответ: (– ; 2) (6; + ).
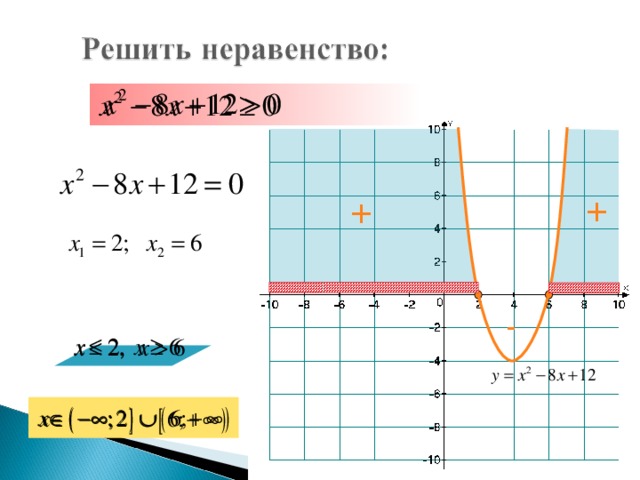
6) x2 – 8x + 12 ≥ 0. Ответ: (– ; 2] [6; + ).
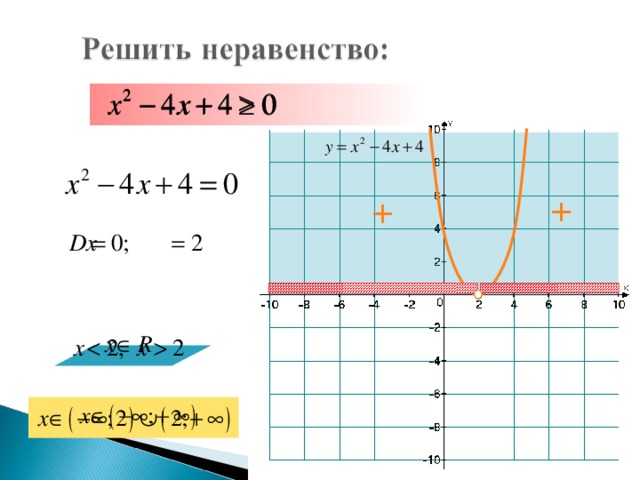
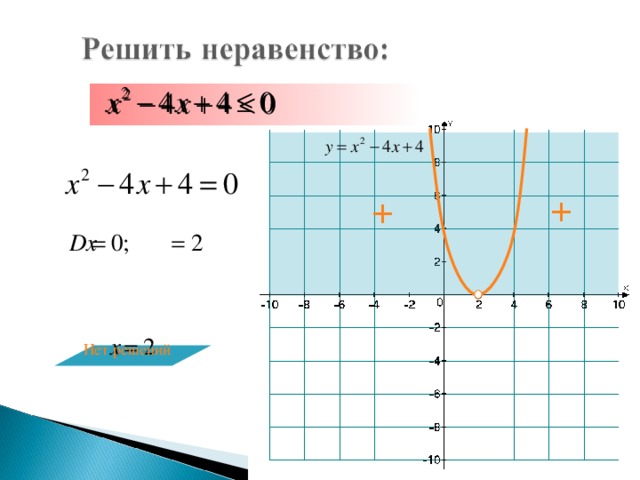
7) х2 – 4х + 4 > 0. Ответ: (– ; 2) (2; + ).
8) х2 – 4х + 4 ≥0. Ответ: (– ; + ).
9) х2 – 4х + 4 < 0. Ответ: нет решений.
10) х2 – 4х + 4 ≤ 0. Ответ: 2
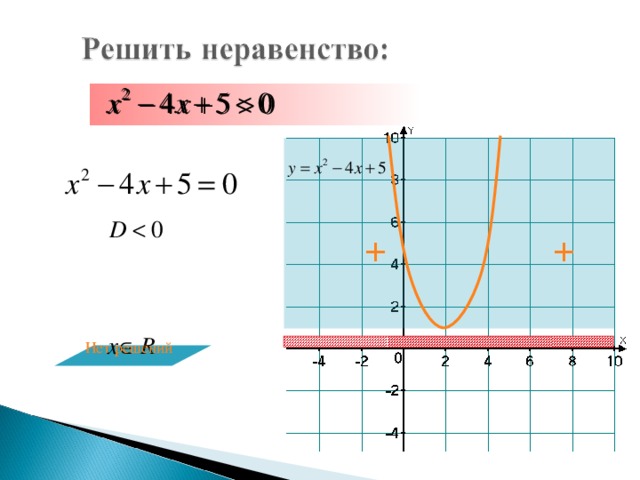
11) х2 – 4х + 5> 0. Ответ: (– ; + ).
12) х2 – 4х + 5 < 0. Ответ: нет решений.
Учитель: Теперь давайте попробуем сформулировать алгоритм решения неравенств второй степени, основанный на свойствах квадратичной функции.
После ответов учащихся учитель предлагает сравнить их с готовым алгоритмом, который лежит у каждого на парте (ПРИЛОЖЕНИЕ 3)
III этап. Усвоение новых знаний. (10 мин.)
На этом этапе учащимся предлагается самостоятельно решить несколько неравенств.
1. х2 + 2х – 48 < 0
2. – 2х2 – 5х +18 ≤ 0
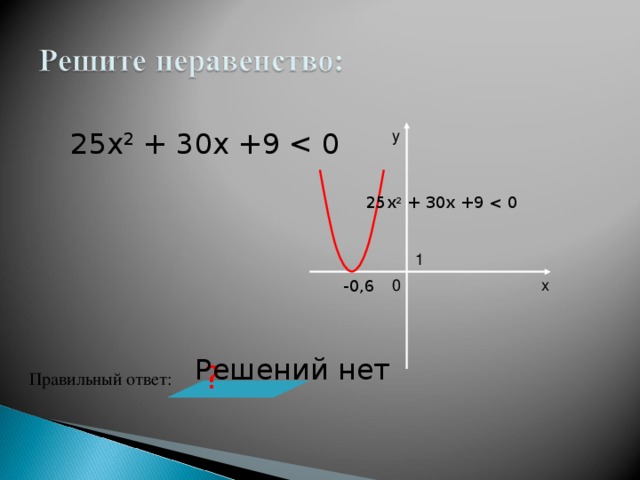
3. 25х2 + 30х +9 < 0
4. – 2х2 +7х > 0
Проверка решения проводится по готовым ответам (слайды 14-17).
IV этап. Итог урок (2-3 мин.) (слайд 18)
- Итак, какие неравенства вы научились сегодня решать?
- Дайте определение квадратного неравенства.
- Как решаются такие неравенства? Кто сможет рассказать алгоритм решения?
V этап. Домашнее задание (1 мин.) (слайд 19)
§6, п. 14, № 304, 306.
Просмотр содержимого документа
«pril3»
Просмотр содержимого документа
«Урок алгебры в 9»
Урок алгебры в 9-м классе по теме "Решение квадратных неравенств"
Большинство жизненных задач решаются как алгебраические уравнения: приведением их к самому простому виду.
Л. Н. Толстой.
Тип: урок изучения нового материала.
Цели урока: 1. Выработка алгоритма решения квадратных неравенств.
2. Формирование навыков решения квадратных неравенств.
3. Развитие навыков самостоятельной работы.
4. Развитие логического мышления, монологической речи.
5. Воспитание внимания, аккуратности.
Оборудование: «Алгебра 9 учебник» (авторы: Макарычев Ю.Н., Миндюк Н.Г. и др.), памятки с алгоритмом решения неравенств второй степени, компьютер, мультимедийный проектор, экран.
ХОД УРОКА
I этап. Организационный момент (1 мин.).
II этап. Объяснение нового материала (30 мин). (ПРИЛОЖЕНИЕ 1)
Учитель: Изучение нового материала мы начнем с понятия неравенства второй степени.
Задание 1. Какие из неравенств вы бы назвали неравенствами второй степени:
1) 6х2 – 13х0; 2) x2 – 3x – 140; 3) (5 + x)(x – 4)7;
4) 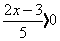 ; 5)
; 5) 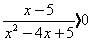 ; 6)
; 6) 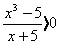 ;
;
7) 8x20; 8) (x – 5)2 – 250; 9) x(x – 9) – x20?
– Теперь давайте сформулируем определение неравенства второй степени:
Определение: Неравенство, левая часть которого есть многочлен второй степени, а правая – нуль, называется неравенством второй степени.
Все квадратные неравенства могут быть приведены к одному из следующих видов:
1) ах2 + bx + c 0;
2) ах2 + bx + c 3) ах2 + bx + c 0;
4) ах2 + bx + c 0.
Задание 2. Какие из чисел являются решениями неравенства  ?
?
| 1 | – 3 | 0 | – 1 | 5 | – 4 | – 2 | 0,5 |
– К квадратным неравенствам нас приводят следующие задачи.
Задание 3. Планируется разбить прямоугольный цветник, который будет примыкать к дому. Заготовленного штакетника хватит на изгородь длиной 20м. Какими должны быть длина и ширина цветника, чтобы он имел площадь не менее: 1) 48 м2; 2) 50 м2.
– Обсудим выполнение этого задания.

Если за х м принять длину стороны цветника, примыкающей к дому, то решение задачи сведется к решению неравенств:
1) (20 – 2х)х 48;
2) (20 – 2х)х 50.
Используя преобразования, эти неравенства можно привести к таким неравенствам второй степени:
1) х2 – 10х + 24 0; 2) х2 – 10х + 25 0.
Попробуем найти способ решения квадратных неравенств, использующий свойства квадратичной функции.
Учащиеся пытаются предложить такой способ. Если идей не возникает, то учитель предлагает выполнить еще одно задание.
Задание 3. На рис. 1 даны графики квадратичных функций. Анализируя эти графики, заполните таблицу. (ПРИЛОЖЕНИЕ 2)
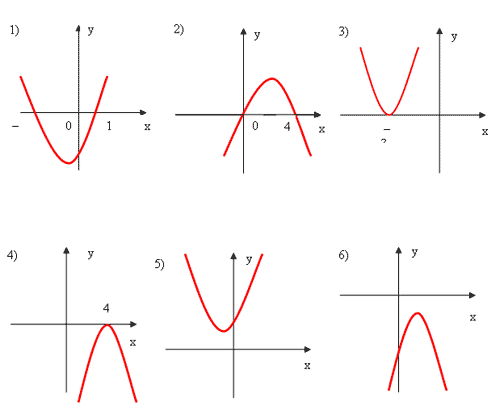
Рис. 1
Учитель: Теперь нам предстоит решить неравенство – х2 + 8x – 12 0.Какая информация о квадратичной функции может оказаться при этом полезной:
знак коэффициента а; направление ветвей параболы;
знак дискриминанта D квадратного трехчлена;
пересечение параболы с осями координат;
координаты вершины параболы;
примерное расположение параболы?
Обязательно ли для решения неравенства строить график соответствующий квадратичной функции? Если да, то с какой точностью выполнять построение?
Далее рассматриваются различные варианты неравенств с подробным решением и записью в тетради (или справочники).(ПРИЛОЖЕНИЕ 1) (слайды 7-13)
Задания:
1) – х2 + 8х – 12 0.
Решение: Пусть у = – х2 + 8х – 12.
а = – 1, а
– х2 + 8х – 12 = 0; D = 82 – 4(– 1)(– 12) = 16 = 42, D 0
x1 = 6; x2 = 2.
Схематически строим график функции.
Ответ: х  (2; 6).
(2; 6).
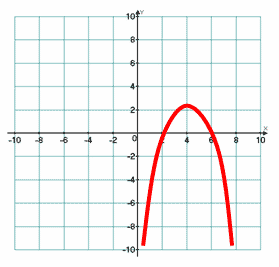
2) – х2 + 8х – 12 ≥ 0. Ответ: [2;6].
3) – х2 + 8х – 12  ; 2)
; 2)  (6; +
(6; +  ).
).
4) – х2 + 8х – 12≤0. Ответ: (–  ; 2]
; 2]  [6; +
[6; +  ).
).
5) x2 – 8x + 12 0. Ответ: (–  ; 2)
; 2)  (6; +
(6; +  ).
).
6) x2 – 8x + 12 ≥ 0. Ответ: (–  ; 2]
; 2]  [6; +
[6; +  ).
).
7) х2 – 4х + 4 0. Ответ: (–  ; 2)
; 2)  (2; +
(2; +  ).
).
8) х2 – 4х + 4 ≥0. Ответ: (–  ; +
; +  ).
).
9) х2 – 4х + 4 10) х2 – 4х + 4 ≤ 0. Ответ: 2
11) х2 – 4х + 5 0. Ответ: (–  ; +
; +  ).
).
12) х2 – 4х + 5
Учитель: Теперь давайте попробуем сформулировать алгоритм решения неравенств второй степени, основанный на свойствах квадратичной функции.
После ответов учащихся учитель предлагает сравнить их с готовым алгоритмом, который лежит у каждого на парте (ПРИЛОЖЕНИЕ 3)
III этап. Усвоение новых знаний. (10 мин.)
На этом этапе учащимся предлагается самостоятельно решить несколько неравенств.
1. х2 + 2х – 48 2. – 2х2 – 5х +18 ≤ 0
3. 25х2 + 30х +9 4. – 2х2 +7х 0
Проверка решения проводится по готовым ответам (слайды 14-17).
IV этап. Итог урок (2-3 мин.) (слайд 18)
Итак, какие неравенства вы научились сегодня решать?
Дайте определение квадратного неравенства.
Как решаются такие неравенства? Кто сможет рассказать алгоритм решения?
V этап. Домашнее задание (1 мин.) (слайд 19)
§6, п. 14, № 304, 306.
Просмотр содержимого презентации
«pril1»




 0; 2) x 2 -3 x -140; 3) (5+ x )( x -4)7; 4) ; 5) ; 6) ; 7) 8 x 2 0; 8)( x -5) 2 -250;" width="640"
0; 2) x 2 -3 x -140; 3) (5+ x )( x -4)7; 4) ; 5) ; 6) ; 7) 8 x 2 0; 8)( x -5) 2 -250;" width="640"




![у – 2х 2 – 5х +18 ≤ 0 – 2х 2 – 5х +18 ≤ 0 -4,5 х 2 [2; +∞) (-∞; -4,5] ? Правильный ответ : 15](https://fsd.kopilkaurokov.ru/uploads/user_file_564cb7fc7329d/img_user_file_564cb7fc7329d_1_14.jpg)
 0 у – 2х 2 +7х 0 0 х 3,5 [3,5; +∞) ? Правильный ответ: 17" width="640"
0 у – 2х 2 +7х 0 0 х 3,5 [3,5; +∞) ? Правильный ответ: 17" width="640"


















