«Кто ничего не замечает,
Тот ничего не изучает,
Тот вечно хнычет и скучает»

Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда ) — древнеегипетское учебное руководство по арифметике и геометрии
Для составления красивых паркетов чаще всего использовали треугольники.

Треугольники в конструкции мостов.
http://mirrorsoul.narod.ru/pictures/P1010096_2.htm

Высоковольтные линии электропередачи.
Треугольники делают конструкции надежными.
http://orsk.ru/index.php?option=com_content&task=view&id=4359&Itemid=110

19 марта 2007 года Шуховской башне на Шаболовке исполнилось 85 лет .
http://www.designet.ru/context/history/?id=31043

Начиная игру в бильярд, необходимо расположить шары в виде треугольника. Для этого используют специальную треугольную рамку.
http://www.bogato.info/index/?node_id=2822
http://www.labirint-shop.ru/screenshot/189362/1/

Расстановка кеглей в игре Боулинг тоже в виде равностороннего треугольника.
http://www.akatuy.ru/bouling.asp?page=./6939/6952/7040/7062
http://rnd.onegintime.ru/game.html?game=3&count=90&limit=10&page_num=8

Треуго́льник — ударный музыкальный инструмент в виде металлического прута , изогнутого в форме треугольника. Один из углов оставлен открытым (концы прута почти касаются).
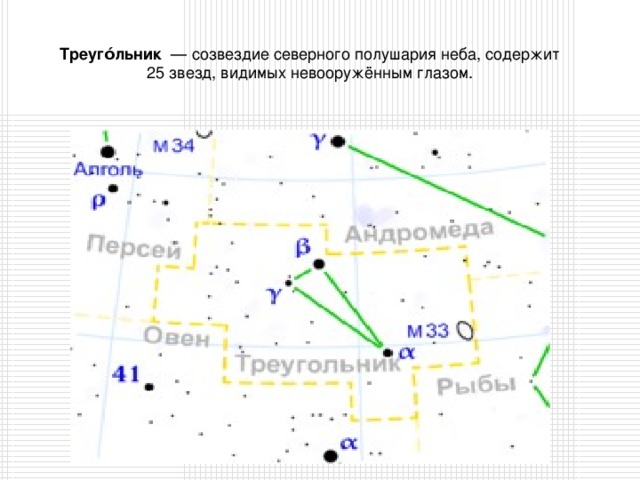
Треуго́льник — созвездие северного полушария неба, содержит 25 звезд, видимых невооружённым глазом.
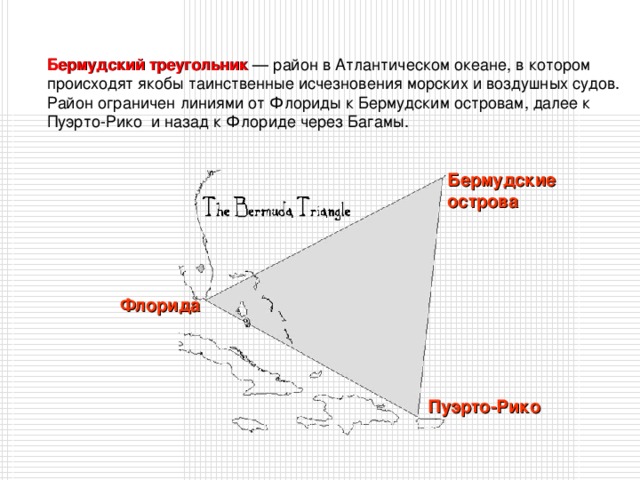
Бермудский треугольник — район в Атлантическом океане , в котором происходят якобы таинственные исчезновения морских и воздушных су дов. Район ограничен линиями от Флор иды к Бермудским острова м , далее к Пуэрто-Рико и назад к Флориде через Багамы .
Бермудские
острова
Флорида
http://ru.wikipedia.org/wiki/%D0%91%D0%B5%D1%80%D0%BC%D1%83%D0%B4%D1%81%D0%BA%D0%B8%D0%B9_%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA
Пуэрто-Рико
А
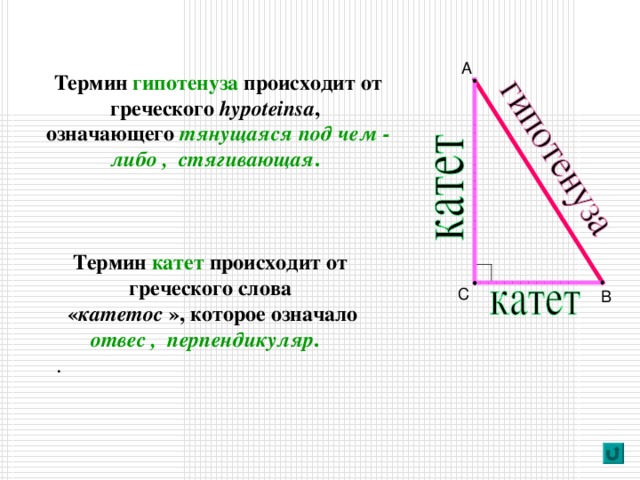
Термин гипотенуза происходит от греческого hypoteinsa ,
означающего тянущаяся под чем - либо , стягивающая .
Термин катет происходит от греческого слова
« катетос », которое означало отвес , перпендикуляр .
.
С
В

Ответьте на вопросы
- Какой треугольник называется прямоугольным?
- Как называются стороны прямоугольного треугольника? Какая сторона большая? Показать по рису нку.

- Прямоугольный треугольник может быть равнобедренным? А равносторонним? Почему?
С
А
В
http://www.wyllf.ru/chtivo/15982-sem-chudes-sveta-v-kartinkakh.html
http://www.infocity.kiev.ua/graf/content/graf049_6.phtml
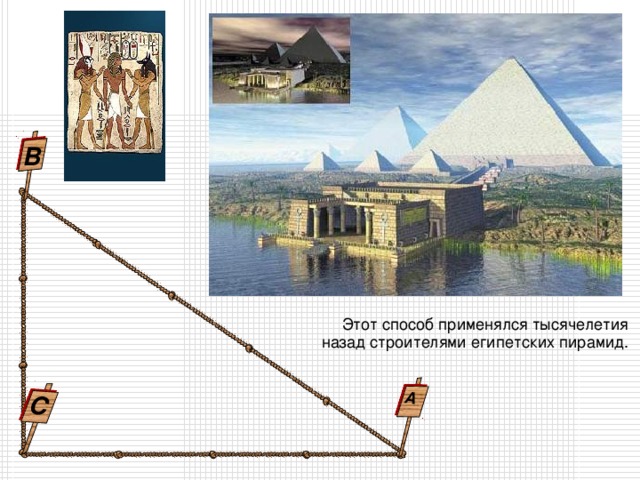
Этот способ применялся тысячелетия
назад строителями египетских пирамид.
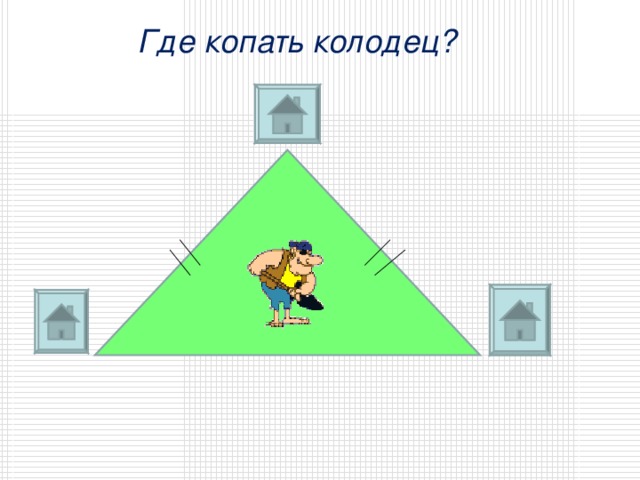
Где копать колодец?
Свойства прямоугольных треугольников.
6
1
5
4
3
2
7
9
8
1 0
11
… по готовым чертежам
1 7
1 6
1 5
1 4
1 3
1 2
Признаки равенства прямоугольного тр-ка.
18
22
21
19
23
20
… по готовым чертежам
25
2 7
24
26
Задания на проверку теоретических знаний.
28
30
29
31
32
33
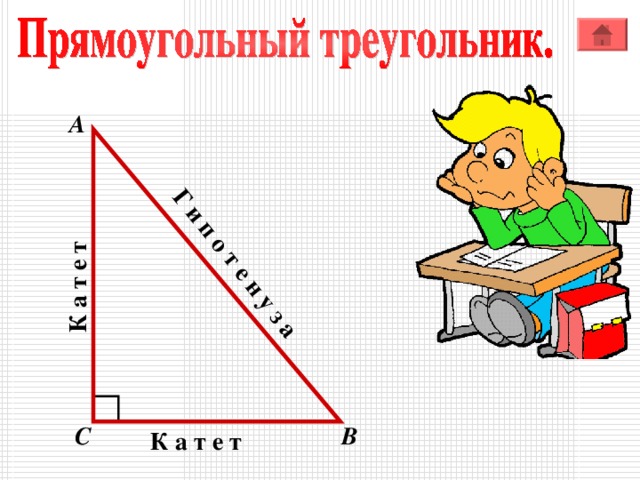
К а т е т
Г и п о т е н у з а
А
В
С
К а т е т
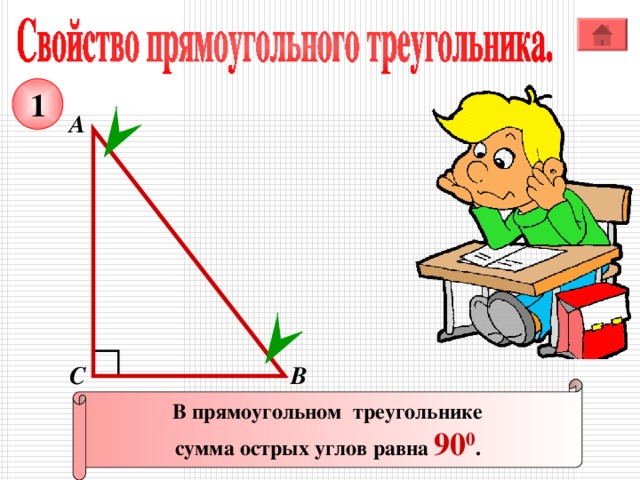
1
А
В
С
В прямоугольном треугольнике
сумма острых углов равна 90 0 .

2
А
30 0
В
С
В прямоугольном треугольнике катет, лежащий
против угла в 30 0 , равен половине гипотенузы

3
А
30 0
В
С
В прямоугольном треугольнике катет, равный
половине гипотенузы лежит против угла в 30 0 .

1
А
А
В
С
С
В
Если катеты одного прямоугольного треугольника
соответственно равны катетам другого,
то такие треугольники равны.
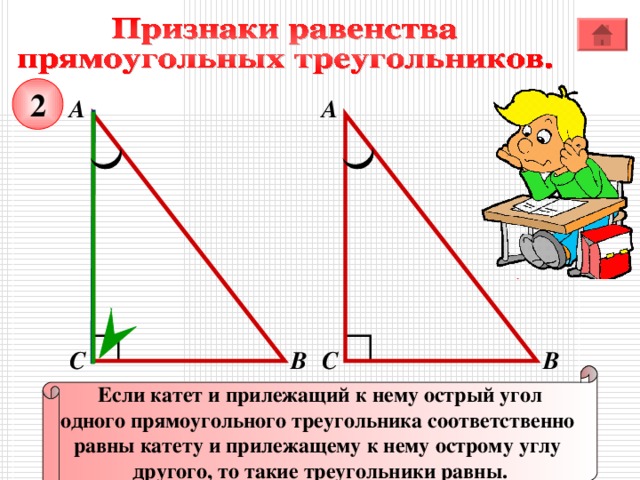
2
А
А
С
В
В
С
Если катет и прилежащий к нему острый угол
одного прямоугольного треугольника соответственно
равны катету и прилежащему к нему острому углу
другого, то такие треугольники равны.
3
А
А
С
В
В
С
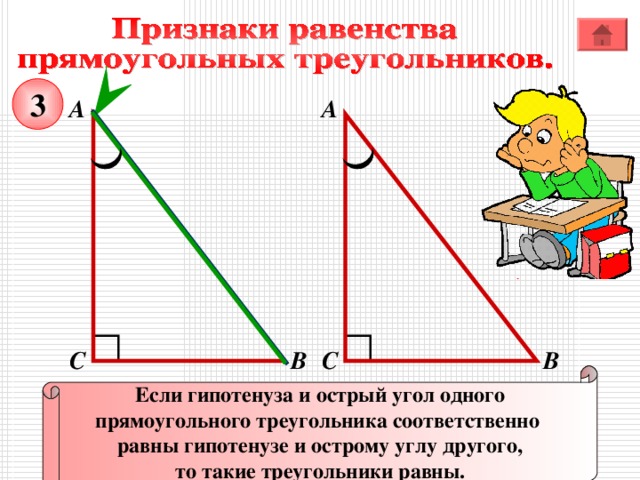
Если гипотенуза и острый угол одного
прямоугольного треугольника соответственно
равны гипотенузе и острому углу другого,
то такие треугольники равны.

4
А
А
В
С
С
В
Если гипотенуза и катет одного прямоугольного
треугольника соответственно равны гипотенузе и
катету другого, то такие треугольники равны.
А
В
С
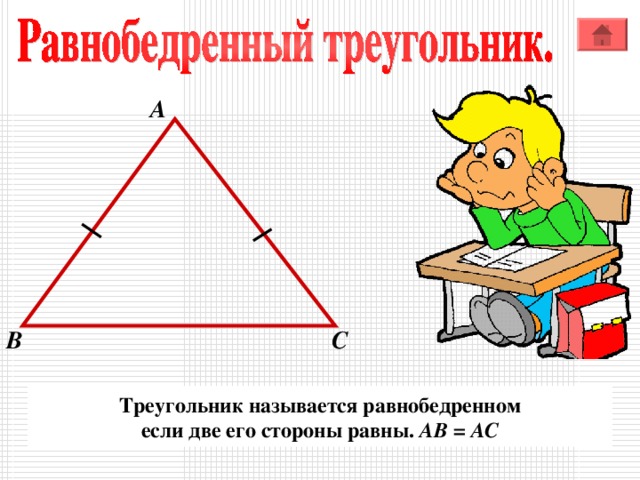
Треугольник называется равнобедренном
если две его стороны равны. АВ = АС
А
М
В
К
С
N
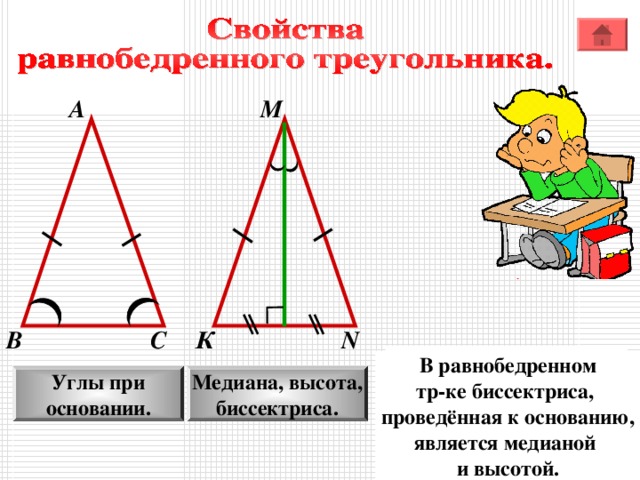
В равнобедренном
треугольнике углы
при основании равны.
В равнобедренном
тр-ке биссектриса,
проведённая к основанию,
является медианой
и высотой.
Углы при
основании.
Медиана, высота,
биссектриса.
В
С
D
А
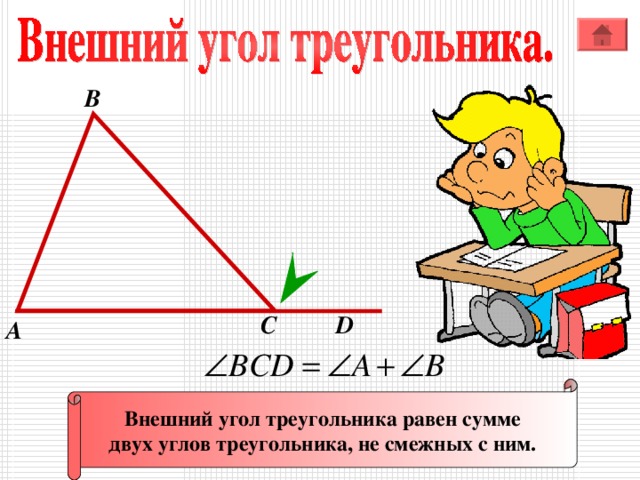
Внешний угол треугольника равен сумме
двух углов треугольника, не смежных с ним.
А
M
В
С
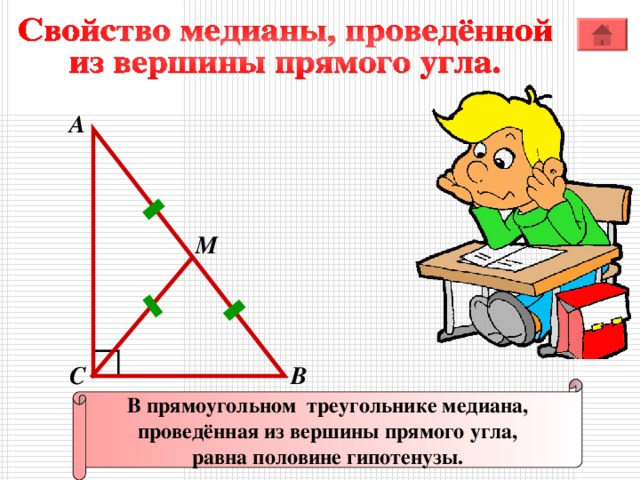
В прямоугольном треугольнике медиана,
проведённая из вершины прямого угла,
равна половине гипотенузы.
А
M
В
С
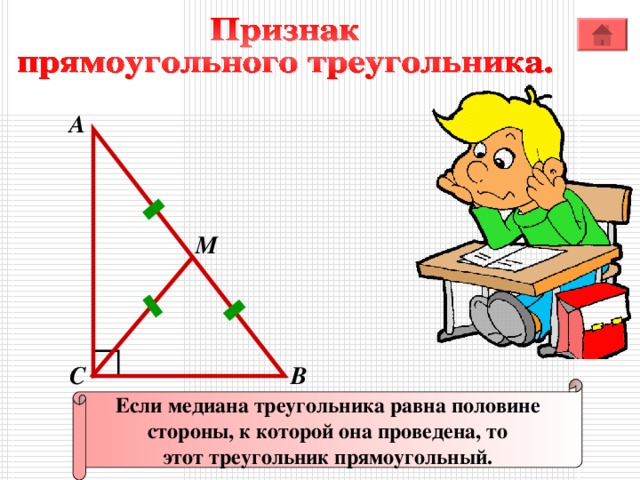
Если медиана треугольника равна половине
стороны, к которой она проведена, то
этот треугольник прямоугольный.
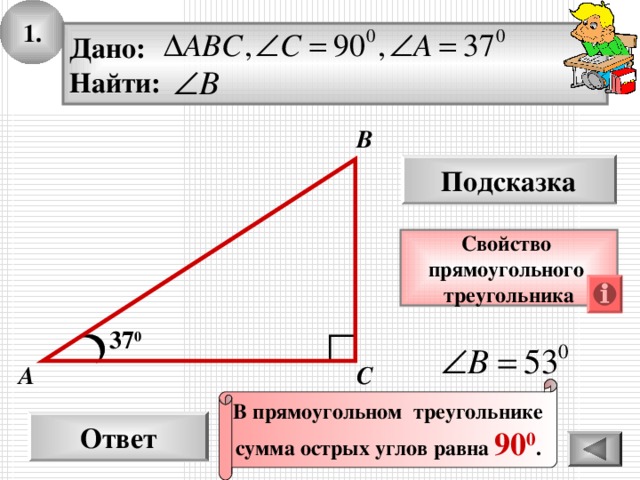
1.
Дано:
Найти:
В
Подсказка
Свойство
прямоугольного
треугольника
37 0
С
А
В прямоугольном треугольнике
сумма острых углов равна 90 0 .
Ответ
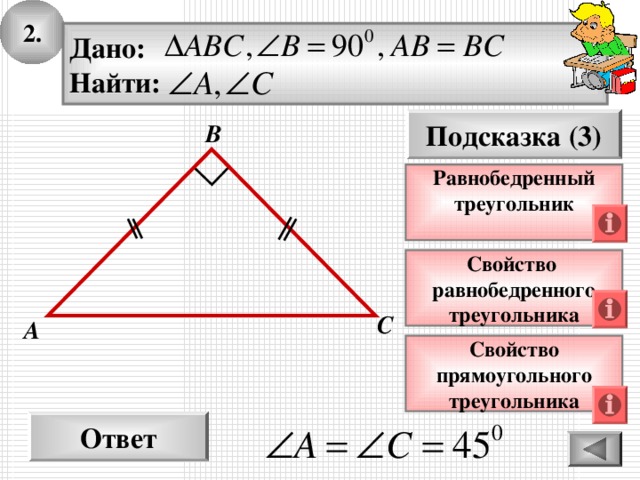
2.
Дано:
Найти:
Подсказка (3)
В
Равнобедренный
треугольник
Свойство
равнобедренного
треугольника
С
А
Свойство
прямоугольного
треугольника
Ответ
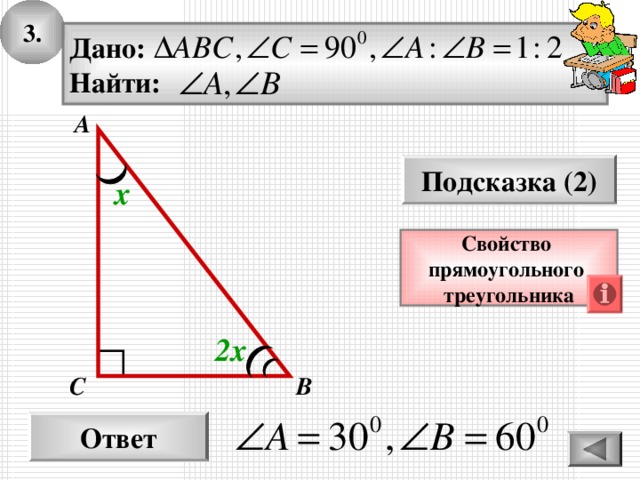
3.
Дано:
Найти:
А
Подсказка (2)
х
Свойство
прямоугольного
треугольника
2х
С
В
Ответ
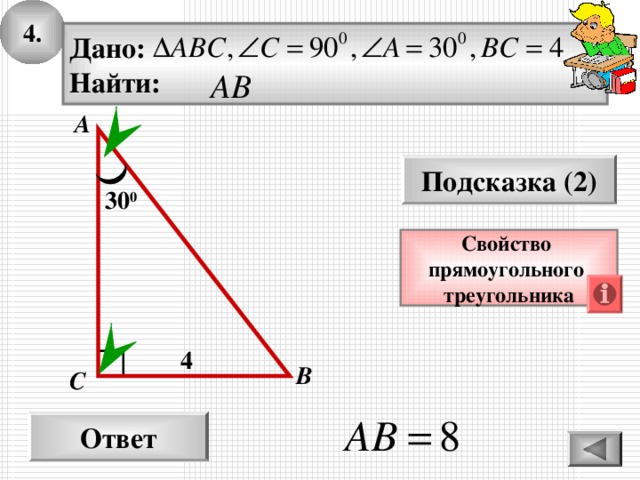
4.
Дано:
Найти:
А
Подсказка (2)
30 0
Свойство
прямоугольного
треугольника
4
В
С
Ответ
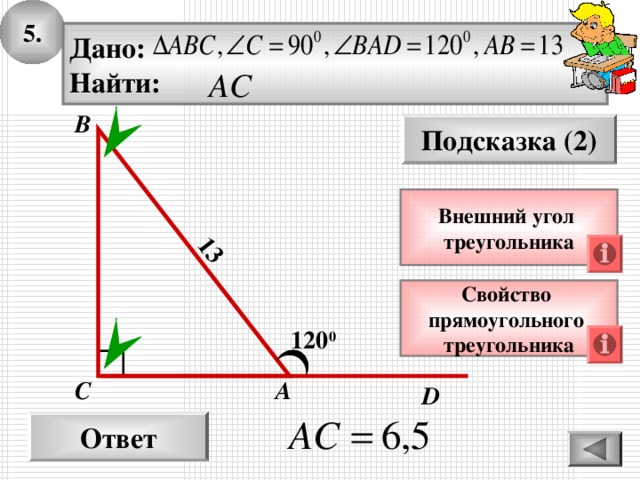
5.
13
Дано:
Найти:
В
Подсказка (2)
Внешний угол
треугольника
Свойство
прямоугольного
треугольника
120 0
С
А
D
Ответ
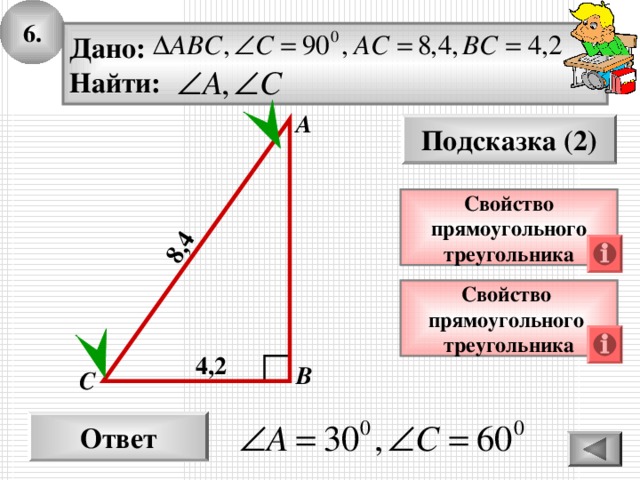
6.
8,4
Дано:
Найти:
А
Подсказка (2)
Свойство
прямоугольного
треугольника
Свойство
прямоугольного
треугольника
4 , 2
В
С
Ответ
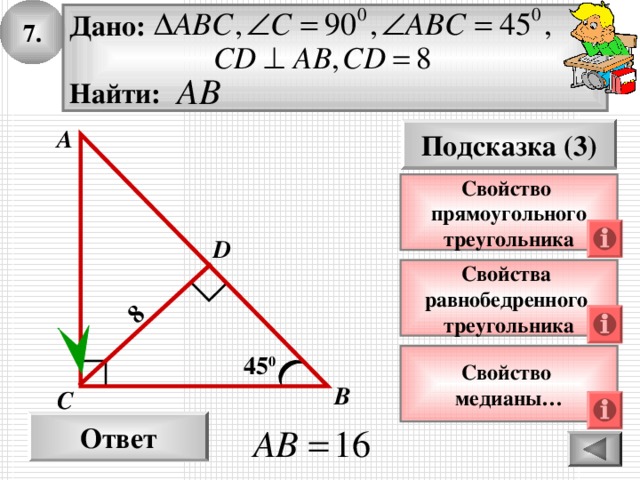
7.
8
Дано:
Найти:
А
Подсказка (3)
Свойство
прямоугольного
треугольника
D
Свойства
равнобедренного
треугольника
45 0
Свойство
медианы…
В
С
Ответ
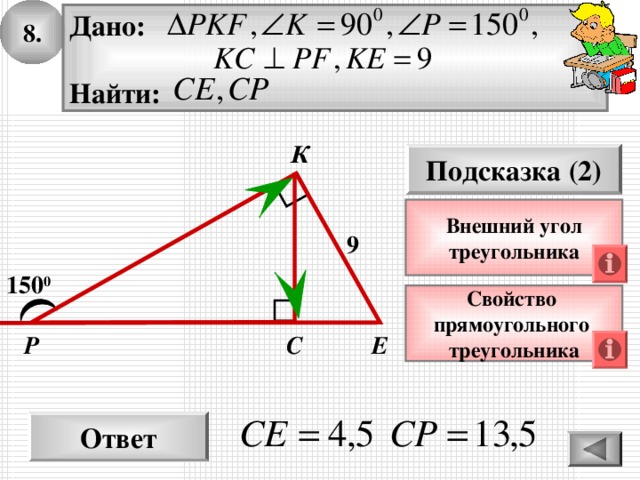
8.
Дано:
Найти:
К
Подсказка (2)
Внешний угол
треугольника
9
150 0
Свойство
прямоугольного
треугольника
С
Р
Е
Ответ
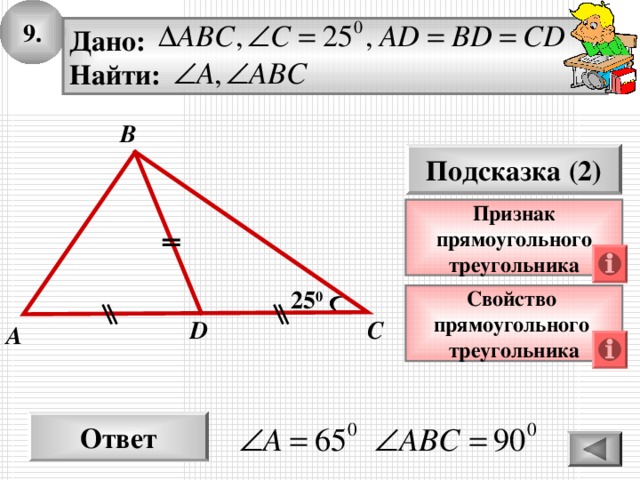
9.
Дано:
Найти:
B
Подсказка (2)
Признак
прямоугольного
треугольника
25 0
Свойство
прямоугольного
треугольника
С
D
A
Ответ

Необходимо по рисунку
записать условие задачи
и ответить на поставленный
вопрос.
В задачах подсказки
отсутствуют.
11
12
13
10
14
15
16
17
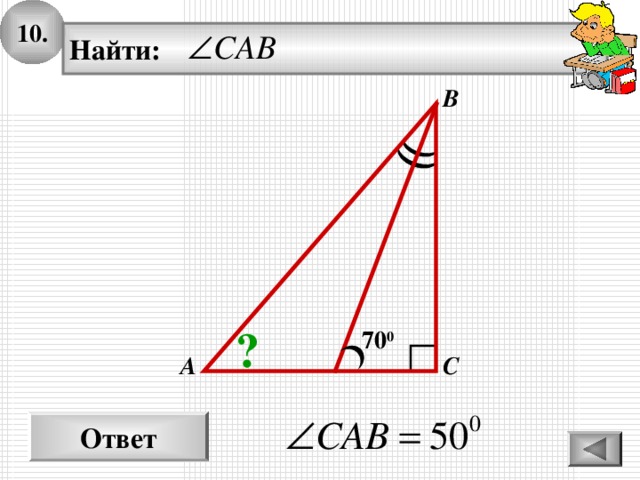
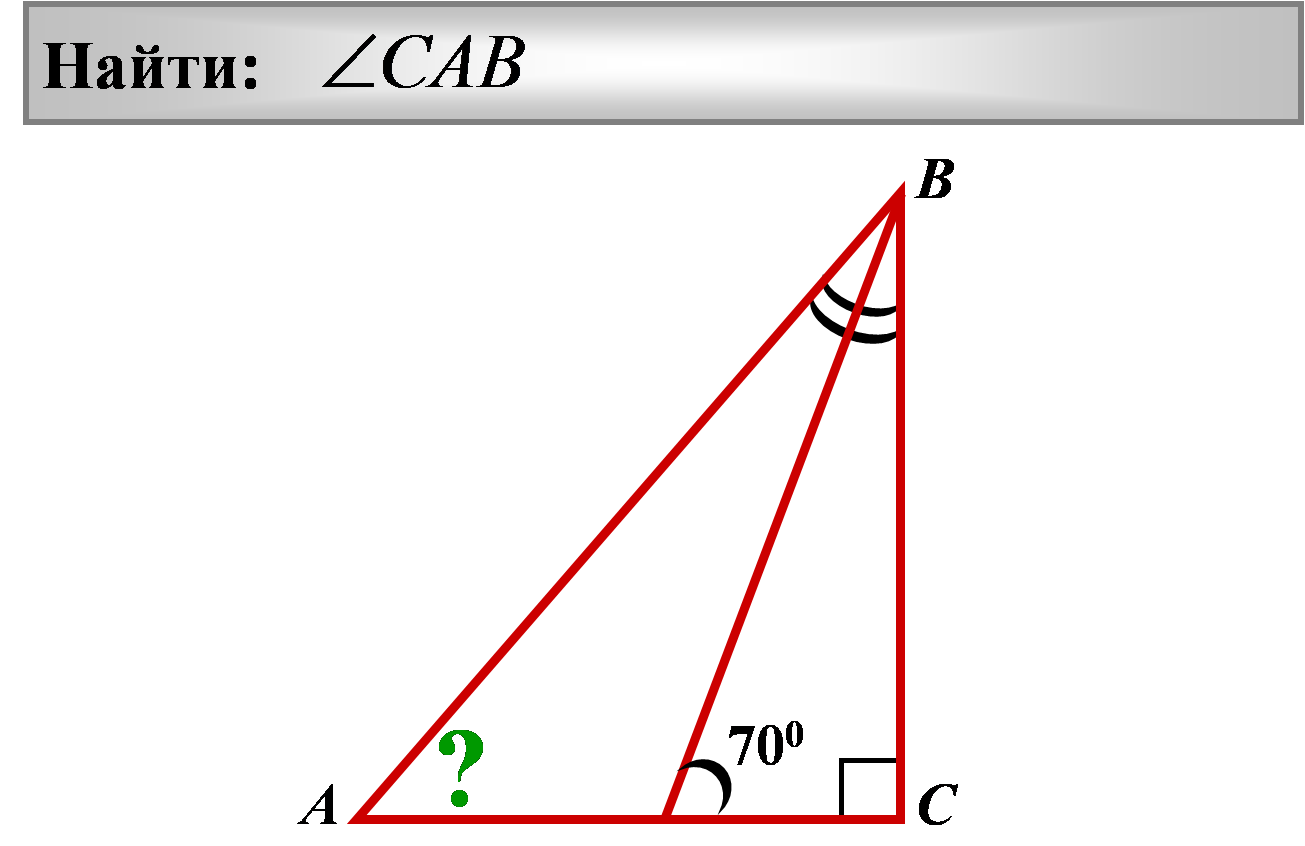
10.
Найти:
В
?
70 0
А
С
Ответ
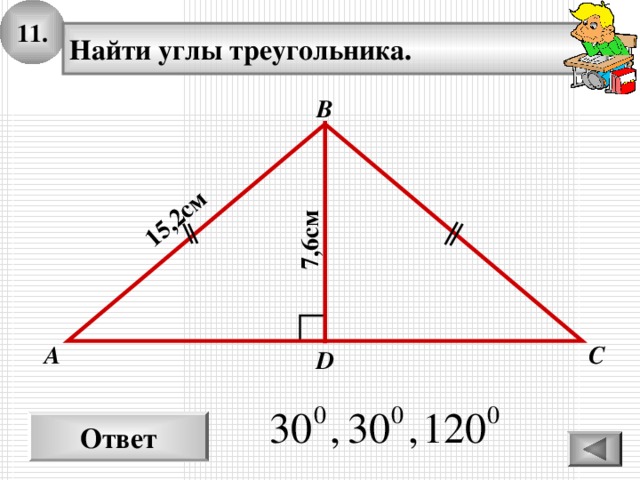
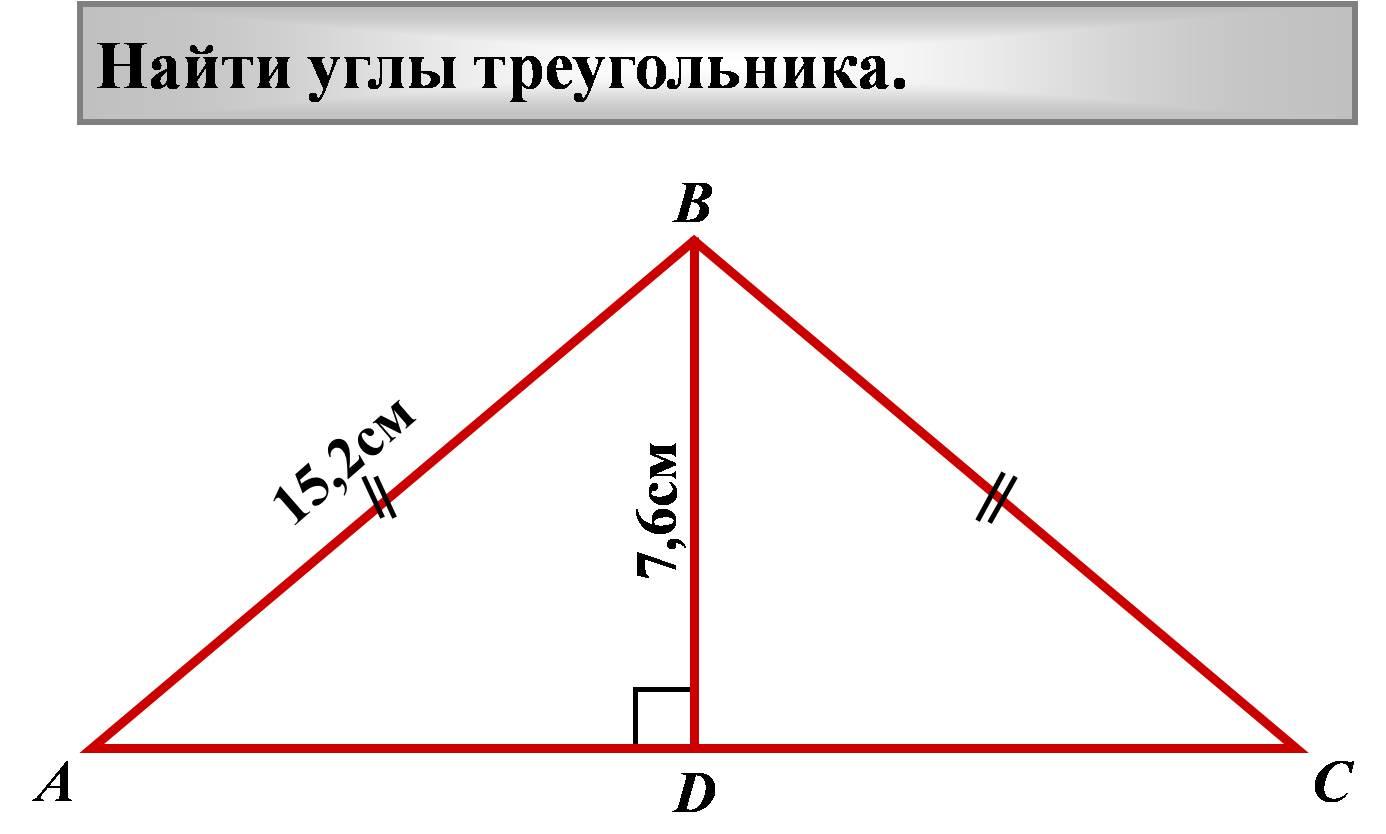
11.
15,2 см
7,6см
Найти углы треугольника.
В
С
А
D
Ответ
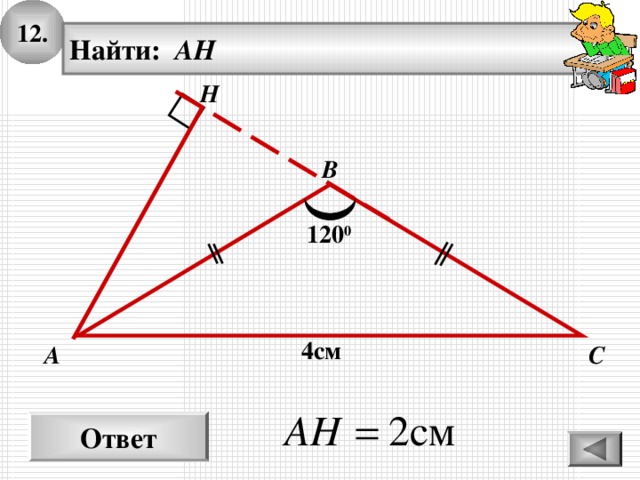
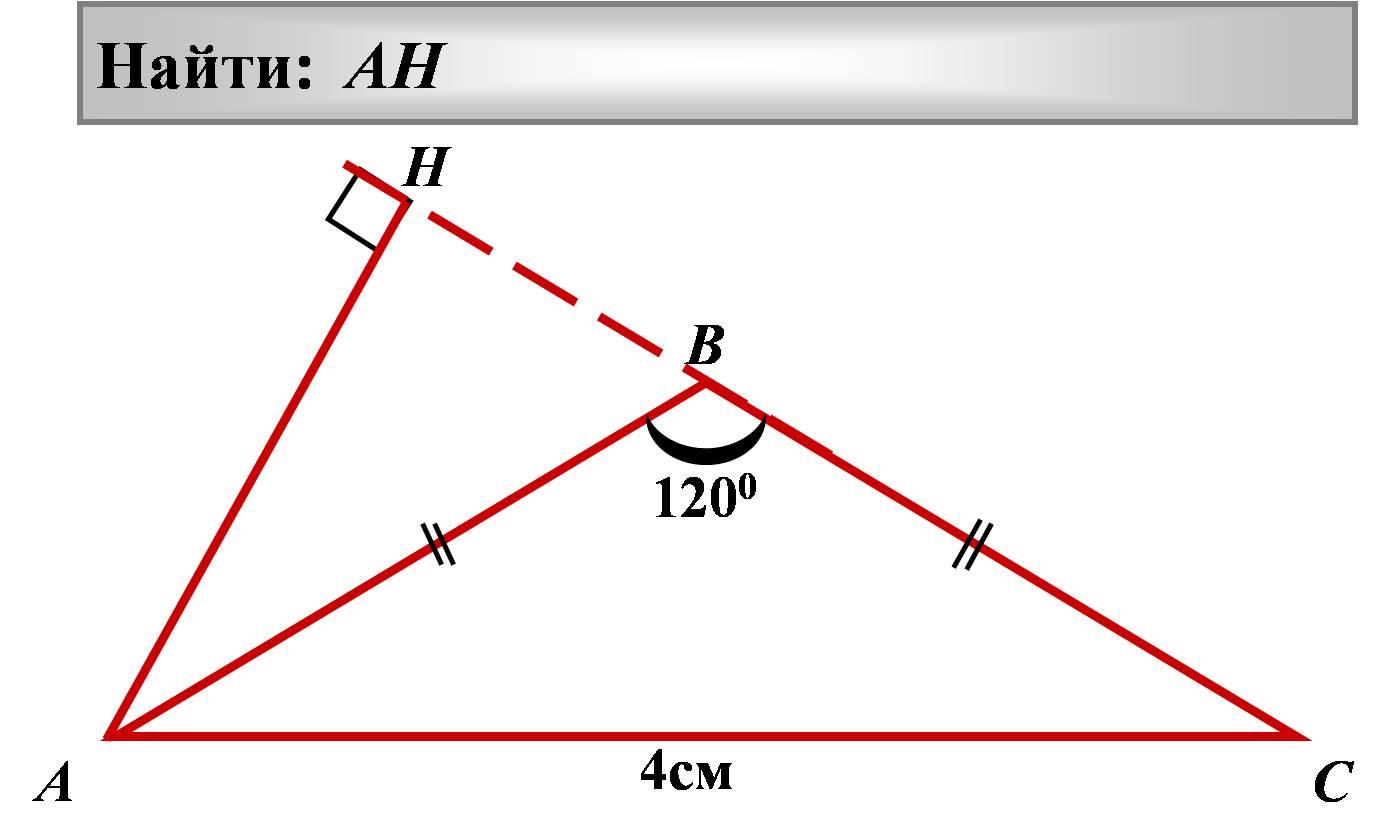
12.
Найти: AH
H
В
12 0 0
4 см
С
А
Ответ
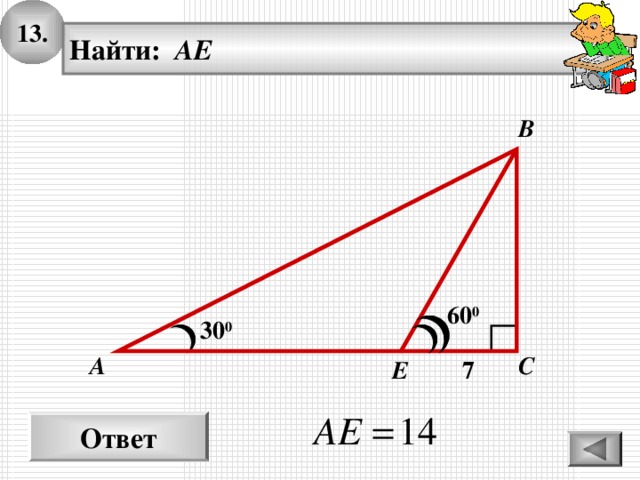
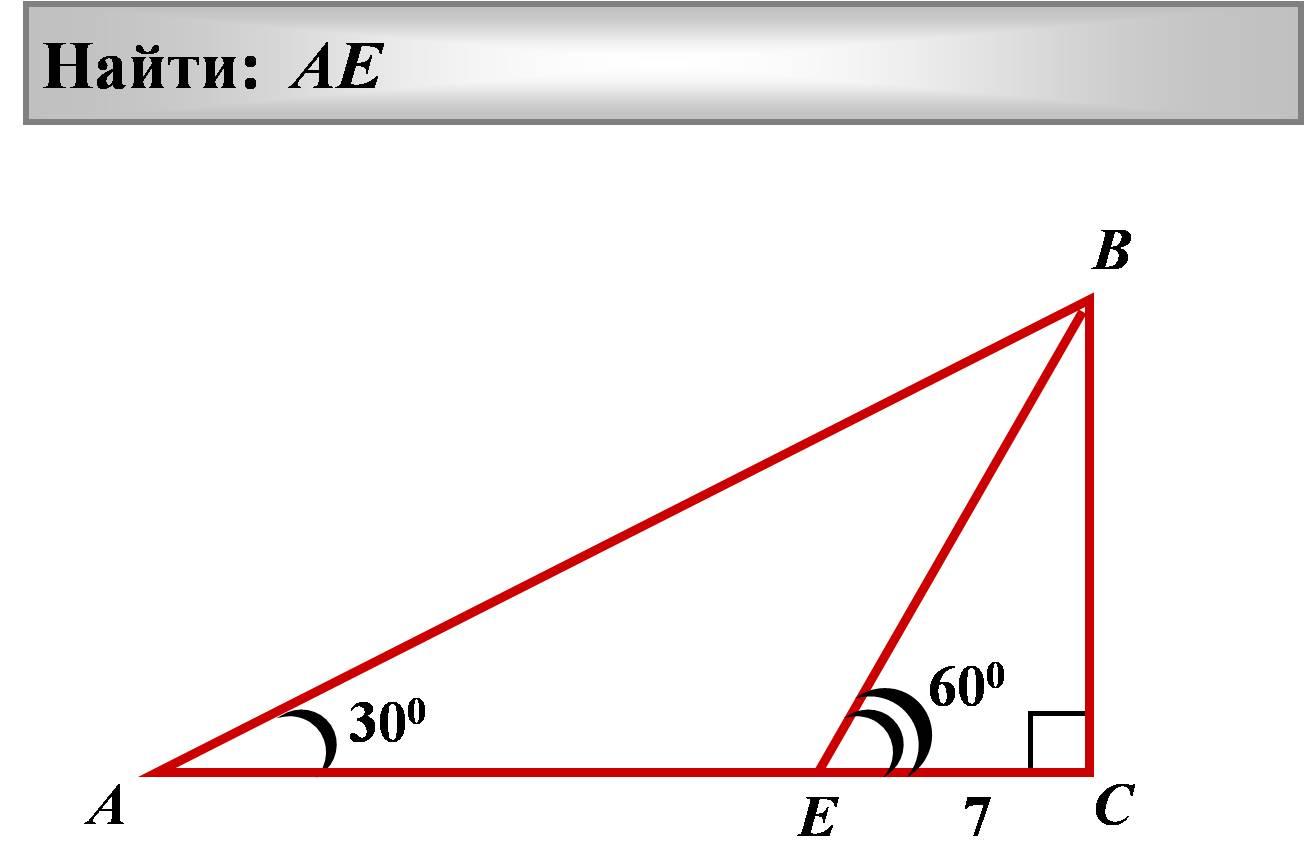
1 3 .
Найти: AE
В
60 0
3 0 0
С
А
7
E
Ответ
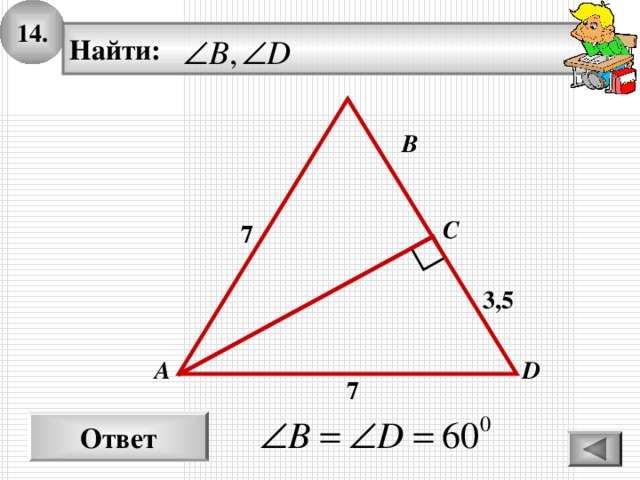
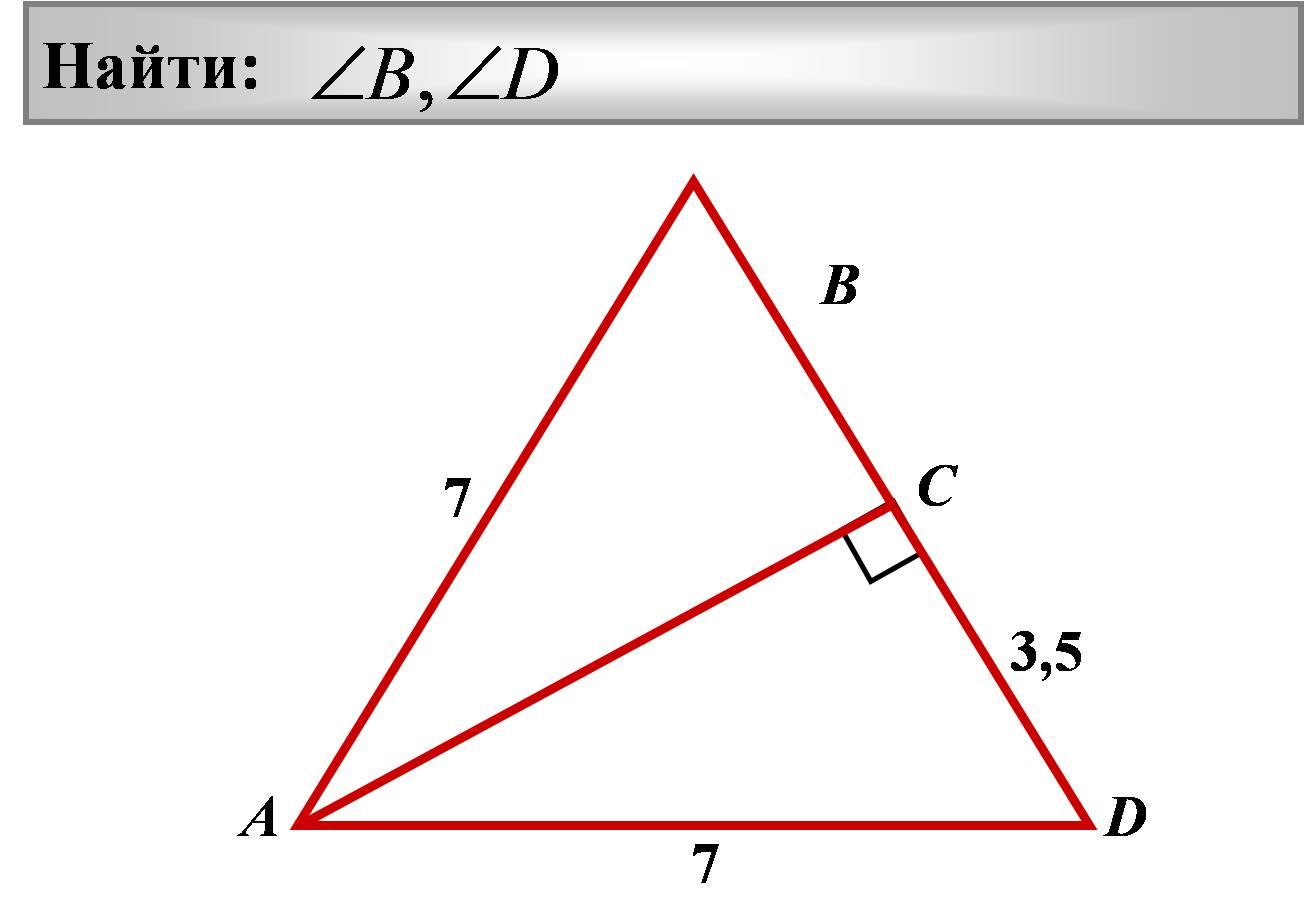
1 4 .
Найти:
В
С
7
3,5
А
D
7
Ответ
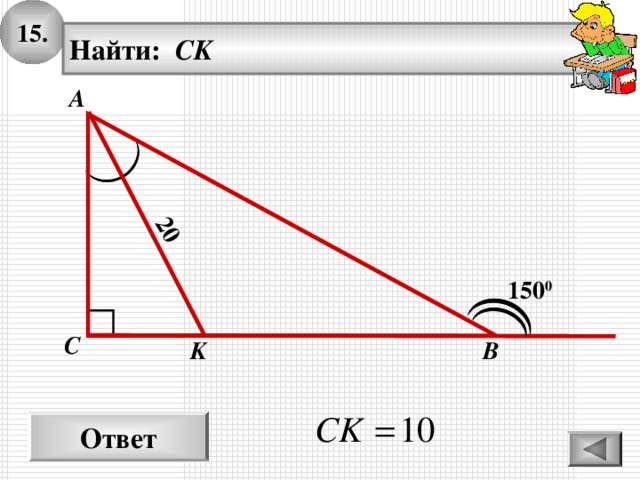
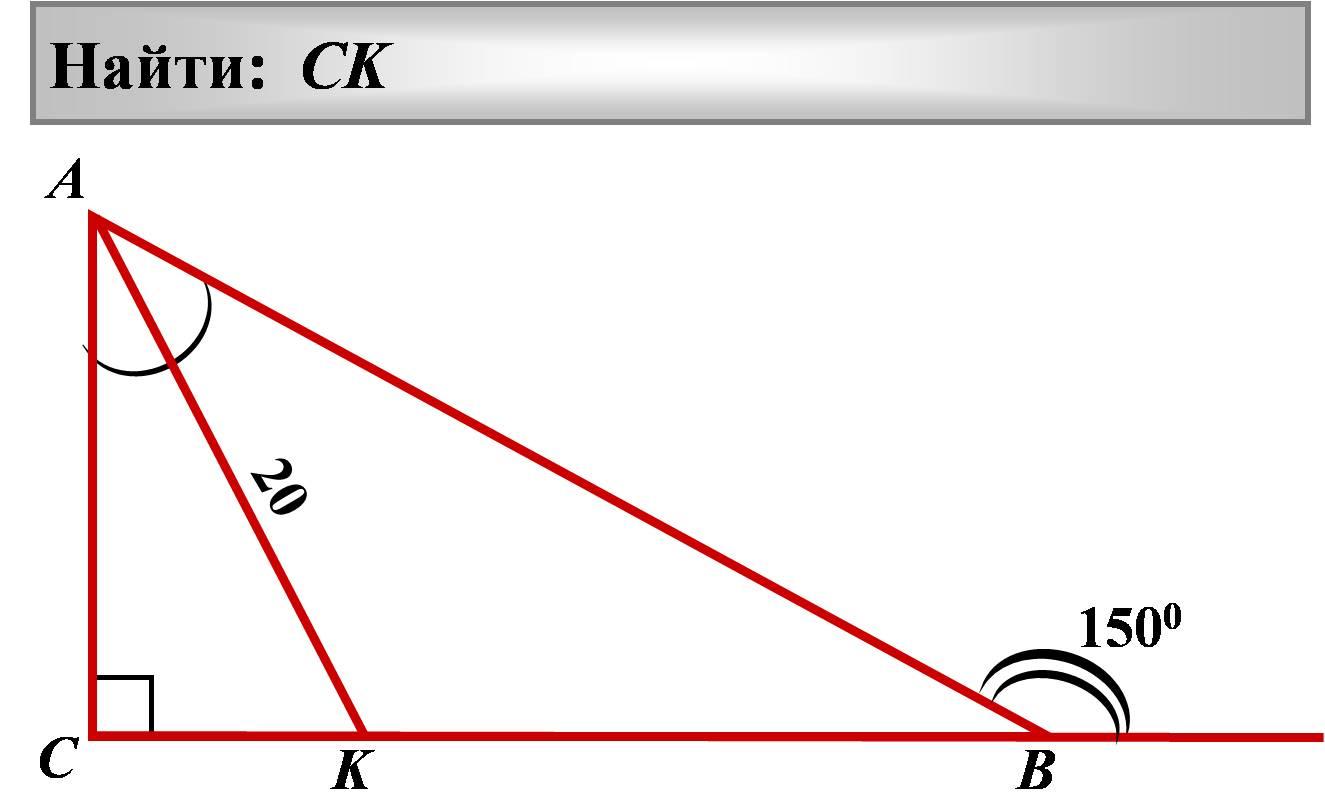
1 5 .
20
Найти: CK
А
150 0
С
В
K
Ответ
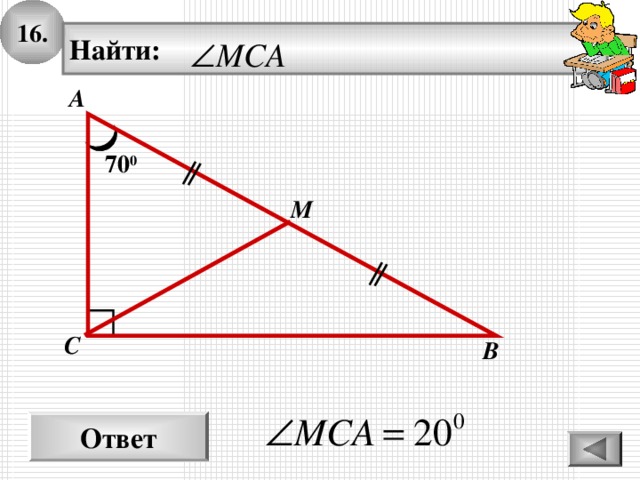
1 6 .
Найти:
А
70 0
M
С
В
Ответ
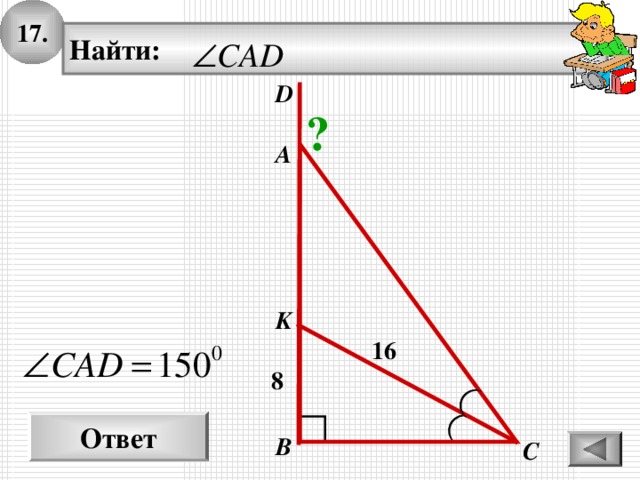
1 7 .
Найти:
D
?
А
K
16
8
Ответ
В
С
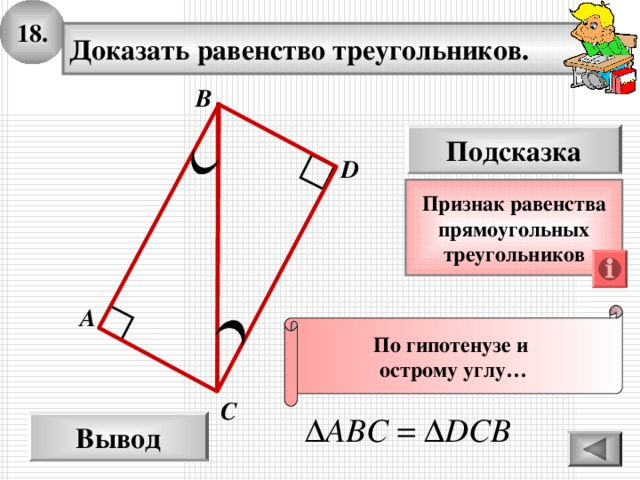
18.
Доказать равенство треугольников.
B
Подсказка
D
Признак равенства
прямоугольных
треугольников
А
По гипотенузе и
острому углу…
С
Вывод
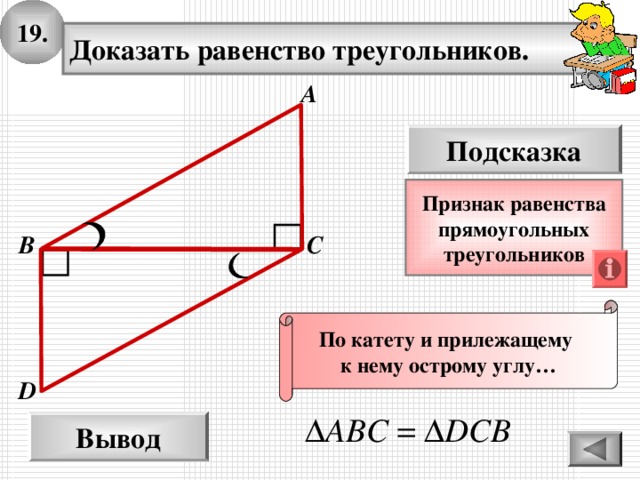
19.
Доказать равенство треугольников.
А
Подсказка
Признак равенства
прямоугольных
треугольников
С
B
По катету и прилежащему
к нему острому углу…
D
Вывод
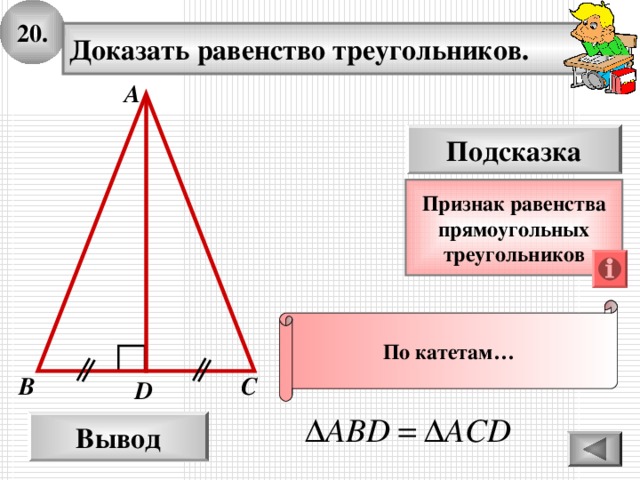
20.
Доказать равенство треугольников.
А
Подсказка
Признак равенства
прямоугольных
треугольников
По катетам…
С
B
D
Вывод
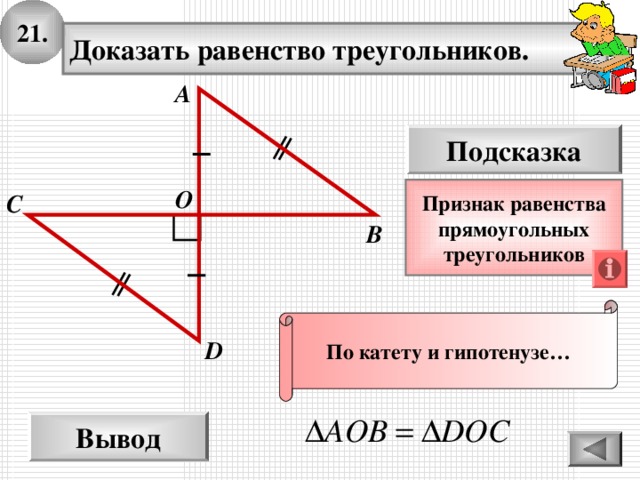
21.
Доказать равенство треугольников.
А
Подсказка
О
Признак равенства
прямоугольных
треугольников
С
B
По катету и гипотенузе…
D
Вывод
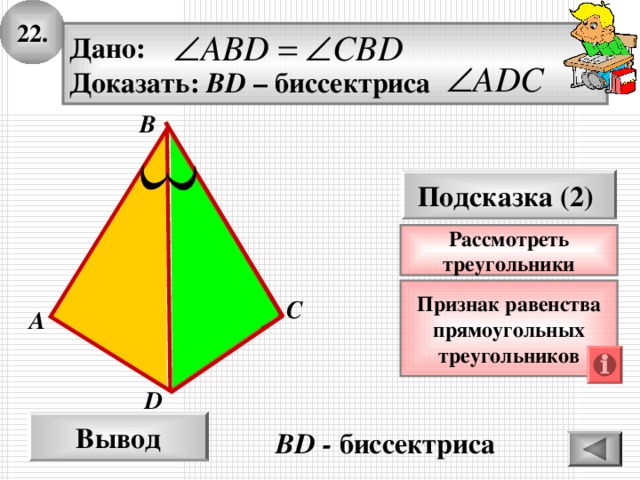
22.
Дано:
Доказать: BD – биссектриса
B
Подсказка (2)
Рассмотреть
треугольники
Признак равенства
прямоугольных
треугольников
C
А
D
Вывод
BD - биссектриса
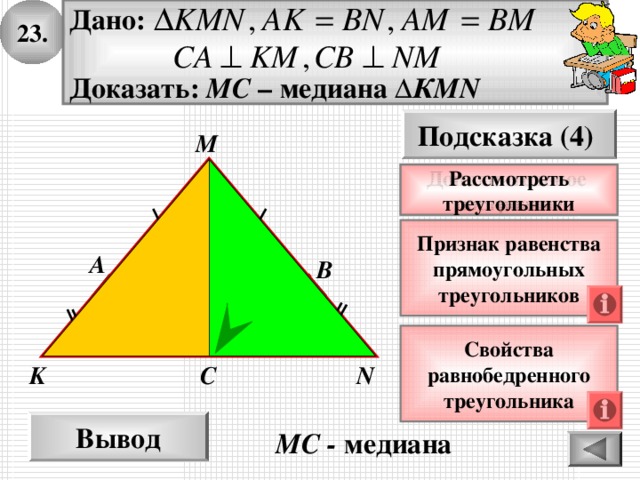
23.
Дано:
Доказать: МС – медиана ∆ КМ N
Подсказка (4)
M
Рассмотреть
треугольники
Дополнительное
построение
Признак равенства
прямоугольных
треугольников
А
B
Свойства
равнобедренного
треугольника
N
K
C
Вывод
МС - медиана

Необходимо по рисунку
записать условие задачи
и ответить на поставленный
вопрос.
В задачах подсказки
отсутствуют.
25
26
27
24
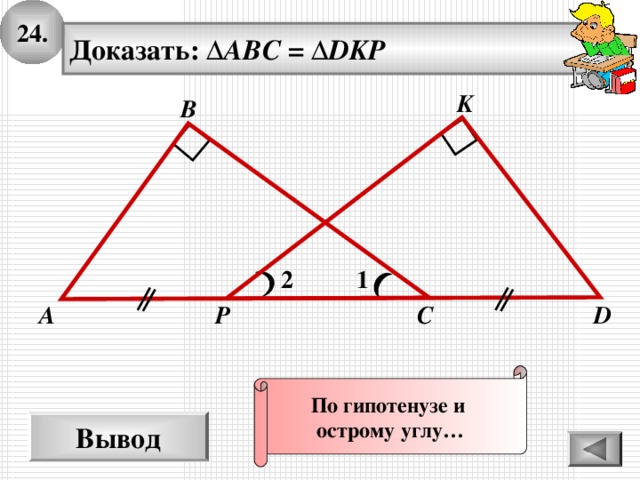
24.
Доказать: ∆ ABC = ∆ DKP
K
В
1
2
D
P
С
А
По гипотенузе и
острому углу…
Вывод
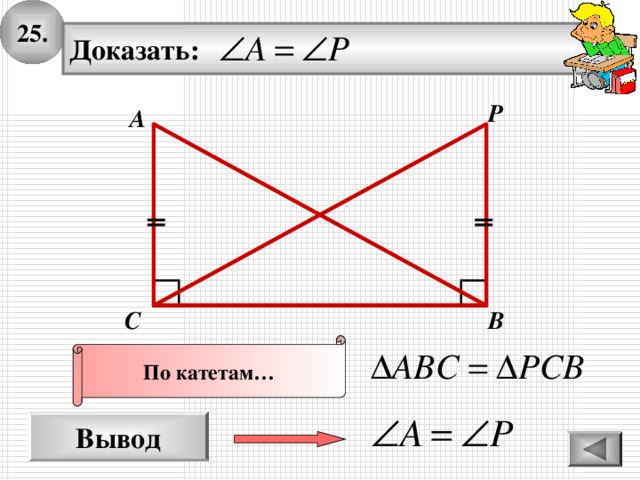
2 5 .
Доказать:
P
А
В
С
По катетам…
Вывод
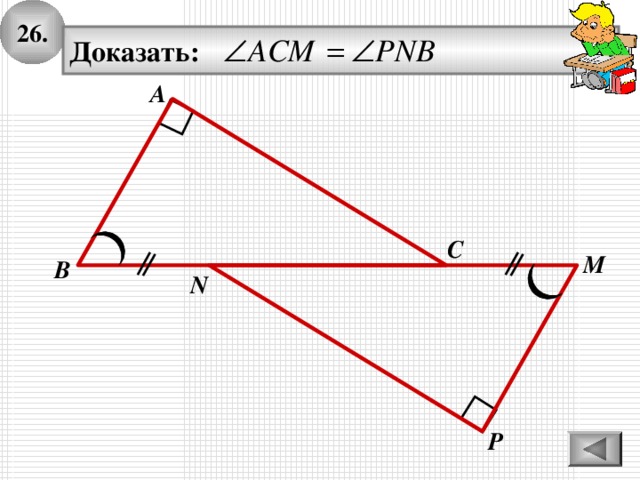
26.
Доказать:
А
С
M
В
N
P
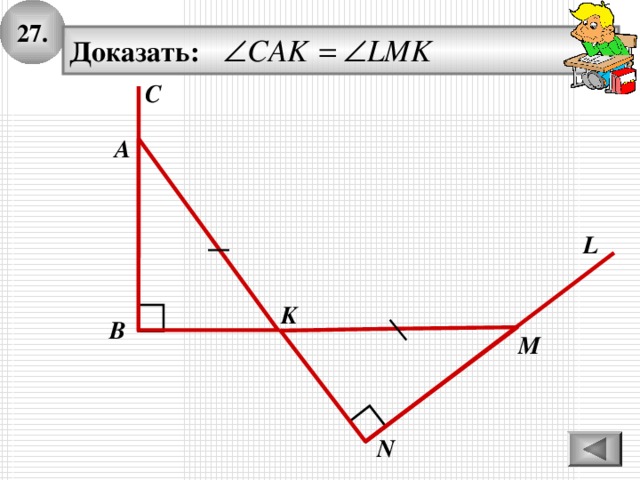
2 7 .
Доказать:
C
А
L
K
B
M
N

В заданиях 28 и 29 необходимо
выбрать верный ответ. Объяснить.
В 3 0 и 3 1 заданиях необходимо
найти градусные меры углов
1, 2 и 3.
В 3 2 и 3 3 заданиях найти градусные
меры углов 1, 2, 3, 4 и 5.
указать равные прямоугольные
треугольники, ответ пояснить.
28
29
3 0
3 1
3 2
3 3
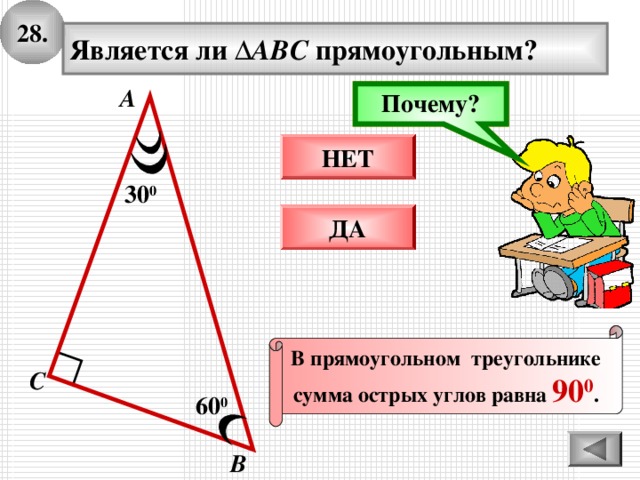
28 .
Является ли ∆ ABC прямоугольным?
А
Почему?
Подумай!
НЕТ
30 0
ДА
В прямоугольном треугольнике
сумма острых углов равна 90 0 .
С
6 0 0
В
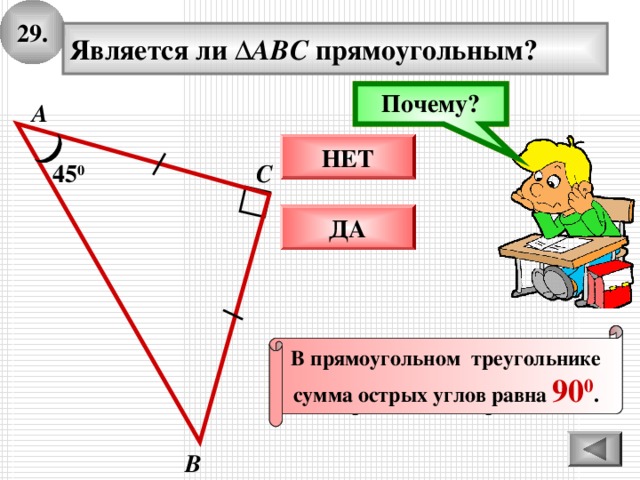
29 .
Является ли ∆ ABC прямоугольным?
Подумай!
Почему?
А
НЕТ
45 0
С
ДА
По определению, треугольник
равнобедренный – углы
при основании равны.
В прямоугольном треугольнике
сумма острых углов равна 90 0 .
В
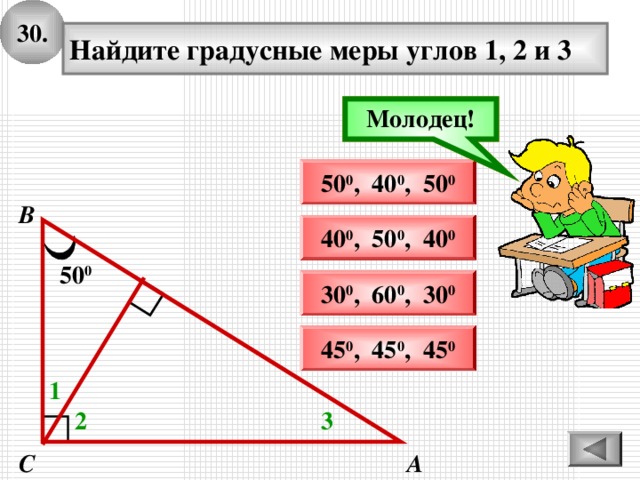
3 0 .
Найдите градусные меры углов 1, 2 и 3
Молодец!
Подумай!
50 0 , 40 0 , 50 0
В
40 0 , 50 0 , 40 0
50 0
30 0 , 60 0 , 30 0
45 0 , 45 0 , 45 0
1
2
3
С
А
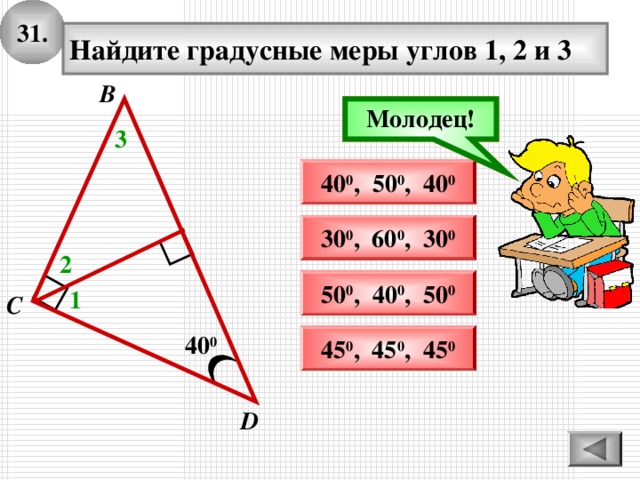
3 1 .
Найдите градусные меры углов 1, 2 и 3
В
Подумай!
Молодец!
3
4 0 0 , 5 0 0 , 4 0 0
30 0 , 60 0 , 30 0
2
5 0 0 , 4 0 0 , 5 0 0
1
С
4 0 0
45 0 , 45 0 , 45 0
D
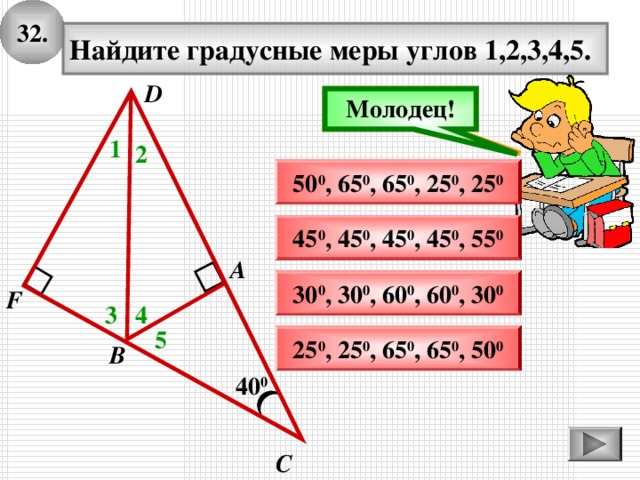
3 2 .
Найдите градусные меры углов 1,2,3,4,5.
D
Подумай!
Молодец!
1
2
50 0 , 65 0 , 6 5 0 , 25 0 , 25 0
45 0 , 45 0 , 45 0 , 45 0 , 55 0
А
30 0 , 30 0 , 60 0 , 6 0 0 , 30 0
F
3
4
5
25 0 , 25 0 , 65 0 , 65 0 , 50 0
В
40 0
С
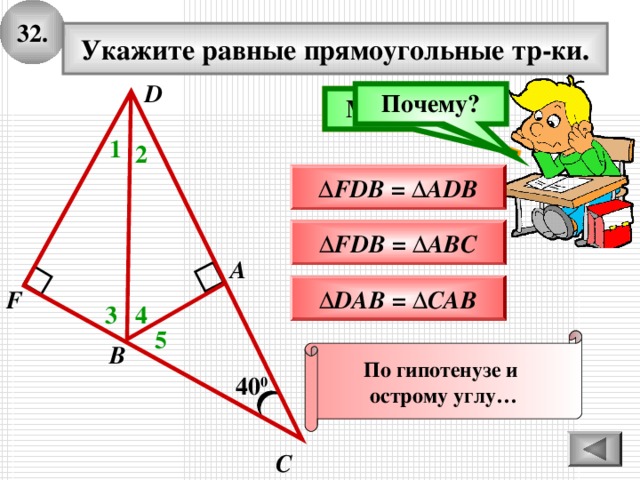
3 2 .
Укажите равные прямоугольные тр-ки.
D
Почему?
Подумай!
Молодец!
1
2
∆ FDB = ∆ ADB
∆ FDB = ∆ ABC
А
∆ DAB = ∆ CAB
F
3
4
5
По гипотенузе и
острому углу…
В
40 0
С
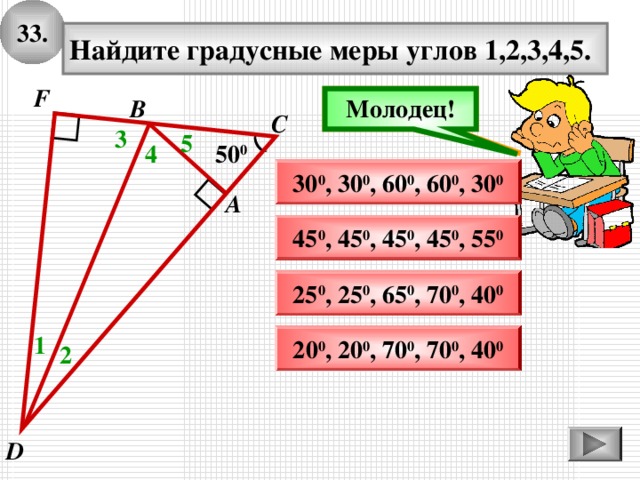
3 3 .
Найдите градусные меры углов 1,2,3,4,5.
F
Подумай!
Молодец!
В
С
3
5
50 0
4
30 0 , 30 0 , 60 0 , 6 0 0 , 30 0
А
45 0 , 45 0 , 45 0 , 45 0 , 55 0
25 0 , 25 0 , 65 0 , 70 0 , 40 0
2 0 0 , 2 0 0 , 70 0 , 70 0 , 4 0 0
1
2
D
3 3 .
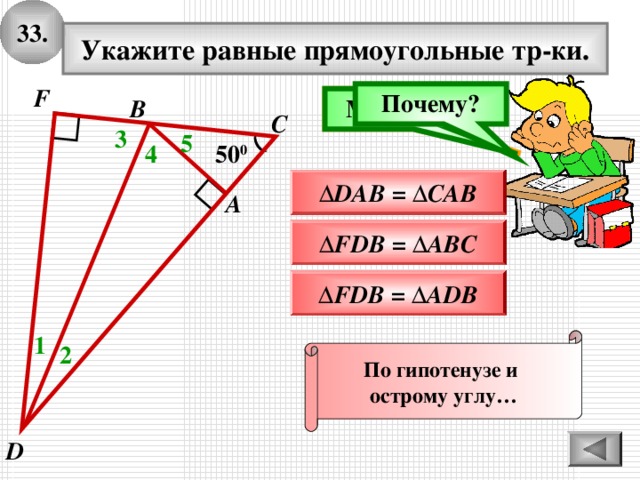
Укажите равные прямоугольные тр-ки.
F
Почему?
В
Подумай!
Молодец!
С
3
5
50 0
4
∆ DAB = ∆ CAB
А
∆ FDB = ∆ ABC
∆ FDB = ∆ ADB
1
По гипотенузе и
острому углу…
2
D

- Н.Ф.Гаврилова «Поурочные разработки по геометрии
7 класс. Универсальное издание. Москва «Вако» 2006г.
2. Картинка:
http://fotki.yandex.ru/users/val-pryanikova/view/543773/?page=3