Урок на тему "Определение арифметической прогрессии"

Определение арифметической прогрессии

Цель урока: определение арифметической прогрессии: вывод формулы n-го члена арифметической прогрессии, формирование умений и навыков решения примеров на применение выведенных формул.

Задачи:

Образовательная: дать определение арифметической прогрессии: вывести формулы n-го члена арифметической прогрессии, формировать умения и навыки решения примеров на применение выведенных формул.

Развивающая: развивать познавательный интерес к предмету, математическую речь учащихся.

Воспитательная: воспитание аккуратности.

ХОД УРОКА:

Организационный момент.

Величие человека - в его способности мыслить. Блез Паскаль

Актуализация прежних знаний учащихся.

Что такое последовательность?
Какие бывают последовательности?

3) Задайте формулой n-го члена последовательность:

Создание проблемной ситуации.

Выявите закономерность и задайте последовательность рекуррентной формулой (работа в парах)

1) 1, 2, 3, 4, 5, …
2) 2, 5, 8, 11, 14,…
3) 8, 6, 4, 2, 0, - 2, …
4) 0,5; 1; 1,5; 2; 2,5; …

Что общего у этих последовательностей?

Такая последовательность называется «арифметическая прогрессия»

Формирование новых знаний учащихся:

Определение: арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.

(ап) – арифметическая прогрессия, если для любого п N выполняется условие ап + 1 = ап + d, где d – некоторое число. Число d называется «разностью арифметической прогрессии», так как из определения следует, что ап + 1 – ап = d.

Примеры арифметических прогрессий:

1) а1 = 1, d = 1.

1; 2; 3; 4; … (последовательные натуральные числа).

2) а1 = 1, d = 2.

1; 3; 5; 6; … (последовательность положительных

нечетных чисел).

3) а1 = –2, d = –2.

–2; –4; –6; –8; –10; … (последовательность отрицательных

четных чисел).

4) а1 = 9, d = 0.

9; 9; 9; 9; … (постоянная последовательность).

5) а1 = 4, d = 0,3.

4; 4,3; 4,6; 4,9; 5,2; …

Обратите внимание, что если d > 0, то арифметическая прогрессия возрастающая, если d < 0 – убывающая, если d = 0 – постоянная.

Физпауза.

Как найти член арифметической прогрессии?

(для того чтобы найти любой член арифметической прогрессии (или задать ее), достаточно знать ее первый член и разность).

Но это очень трудоемко, например:

(ап) – арифметическая прогрессия, где а1 = 2, d = 27. Найти сотый член.

Пользуясь определением, нам нужно сделать 100 шагов. Это громоздко. Хотелось бы знать формулу для нахождения любого члена арифметической прогрессии только по первому члену, разности и порядковому номеру искомого члена.

Для вывода формулы пользуемся определением арифметической прогрессии:

а1

а2 = а1 + d

а3 = а2 + d = (а1 + d) + d = а1 + 2d

а4 = а3 + d = (а1 + 2d) + d = а1 + 3d

а5 = а4 + d = (а1 + 3d) + d = а1 + 4d

а6 = … = а1 + 5d

… …

– формула п-го члена

арифметической прогрессии.

Формирование умений и навыков

Работа с учебником: № 343 (а, б), № 344 (а, в, д).

Самостоятельное решение с последующей проверкой слабым учащимся. Сильным №349

Решение у доски с объяснением № 345.

5. Итоги урока.

Что называется арифметической прогрессией?
Как задается арифметическая прогрессия?
Назовите формулу п-го члена арифметической прогрессии.

7. Рефлексия.

Какую цель вы ставили перед собой на уроке?

Вы достигли поставленной цели?

Что помогало выполнять задание?

Проанализируйте свою работу на уроке.

6. Домашнее задание: № 575 (в, г); № 576 (б)

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«арифметическая прогрессия»

Определение арифметической прогрессии

Задачи:

Развивающая: развивать познавательный интерес к предмету, математическую речь учащихся.

Воспитательная: воспитание аккуратности.

ХОД УРОКА:

Организационный момент.

Величие человека - в его способности мыслить. Блез Паскаль

Актуализация прежних знаний учащихся.

Что такое последовательность?
Какие бывают последовательности?

3) Задайте формулой n-го члена последовательность:

Создание проблемной ситуации.

Выявите закономерность и задайте последовательность рекуррентной формулой (работа в парах)

1) 1, 2, 3, 4, 5, …
2) 2, 5, 8, 11, 14,…
3) 8, 6, 4, 2, 0, - 2, …
4) 0,5; 1; 1,5; 2; 2,5; …

Что общего у этих последовательностей?

Такая последовательность называется «арифметическая прогрессия»

Формирование новых знаний учащихся:

Определение: арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.

(а_п) – арифметическая прогрессия, если для любого п 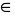N выполняется условие а_п_{+ 1} = а_п + d, где d – некоторое число. Число d называется «разностью арифметической прогрессии», так как из определения следует, что а_п_{+ 1} – а_п = d.

Примеры арифметических прогрессий:

1) а₁ = 1, d = 1.

1; 2; 3; 4; … (последовательные натуральные числа).

2) а₁ = 1, d = 2.

1; 3; 5; 6; … (последовательность положительных

нечетных чисел).

3) а₁ = –2, d = –2.

–2; –4; –6; –8; –10; … (последовательность отрицательных

четных чисел).

4) а₁ = 9, d = 0.

9; 9; 9; 9; … (постоянная последовательность).

5) а₁ = 4, d = 0,3.

4; 4,3; 4,6; 4,9; 5,2; …

Обратите внимание, что если d 0, то арифметическая прогрессия возрастающая, если d d = 0 – постоянная.

Физпауза.

Как найти член арифметической прогрессии?

Но это очень трудоемко, например:

(а_п) – арифметическая прогрессия, где а₁ = 2, d = 27. Найти сотый член.

Для вывода формулы пользуемся определением арифметической прогрессии:

а₁

а₂ = а₁ + d

а₃ = а₂ + d = (а₁ + d) + d = а₁ + 2d

а₄ = а₃ + d = (а₁ + 2d) + d = а₁ + 3d

а₅ = а₄ + d = (а₁ + 3d) + d = а₁ + 4d

а₆ = … = а₁ + 5d

… …

– формула п-го члена

арифметической прогрессии.

Формирование умений и навыков

Работа с учебником: № 343 (а, б), № 344 (а, в, д).

Самостоятельное решение с последующей проверкой слабым учащимся. Сильным №349

Решение у доски с объяснением № 345 .

5. Итоги урока.

Что называется арифметической прогрессией?
Как задается арифметическая прогрессия?
Назовите формулу п-го члена арифметической прогрессии.

7. Рефлексия.

Какую цель вы ставили перед собой на уроке?

Вы достигли поставленной цели?

Что помогало выполнять задание?

Проанализируйте свою работу на уроке.

6. Домашнее задание: № 575 (в, г); № 576 (б)

Просмотр содержимого презентации
«9 класс определение арифметической прогрессии»

Величие человека - в его способности мыслить. Блез Паскаль

Проследите закономерность

задайте последовательность

формулой

1) 1, 2, 3, 4, 5, …

2) 2, 5, 8, 11, 14,…

3) 8, 6, 4, 2, 0, - 2, …

4) 0,5; 1; 1,5; 2; 2,5; …

Арифметическая прогрессия

Определение арифметической прогрессии

Арифметическая прогрессия – это числовая последовательность, каждый член которой, начиная со второго равен предыдущему сложенному с одним и тем же числом.

- разность арифметической прогрессии (число)

Определение арифметической прогрессии

- арифметическая прогрессия, если для всех натуральных n выполняется равенство

Разность арифметической прогрессии

- прогрессия возрастающая

- прогрессия убывающая

Назвать первый член и разность арифметической прогрессии:

6, 8, 10, 12, …
7, 10, 13, 16, …
25, 21, 17, 13, …
-12, -9, -6, -3, …

Запишите первые пять членов арифметической прогрессии, если

Ответ: 7; 12; 17; 22; 27

2) ,

Ответ: 11; 9; 7; 5; 3

Задание арифметической прогрессии формулой n – го члена

первый член арифметической прогрессии

разность арифметической прогрессии

Подведем итог

- разность арифметической прогрессии (число)

Подведем итог

- разность арифметической прогрессии (число)

Формула n-го члена арифметической прогрессии

Предмет: Математика

Категория: Уроки

Целевая аудитория: 9 класс

Скачать
Урок на тему "Определение арифметической прогрессии"

Автор: Янковская Галина Дмитриевна

Дата: 25.10.2015

Номер свидетельства: 243447

Похожие файлы

Презентация на тему "Определение арифметической прогрессии. Формула n-го члена"

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(146) "Презентация на тему "Определение арифметической прогрессии. Формула n-го члена" "
    ["seo_title"] => string(93) "priezientatsiia-na-tiemu-opriedielieniie-arifmietichieskoi-proghriessii-formula-n-gho-chliena"
    ["file_id"] => string(6) "189150"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(11) "presentacii"
    ["date"] => string(10) "1426830769"
  }
}

Конспект урока по теме "Определение арифметической прогрессии. Формула n-го члена"

object(ArrayObject)#875 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(151) "Конспект урока по теме "Определение арифметической прогрессии. Формула n-го члена" "
    ["seo_title"] => string(94) "konspiekt-uroka-po-tiemie-opriedielieniie-arifmietichieskoi-proghriessii-formula-n-gho-chliena"
    ["file_id"] => string(6) "116851"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1412616482"
  }
}

Урок алгебры в 9-м классе по теме "Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии"

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(218) "Урок алгебры в 9-м классе по теме "Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии" "
    ["seo_title"] => string(138) "urok-alghiebry-v-9-m-klassie-po-tiemie-opriedielieniie-arifmietichieskoi-proghriessii-formula-n-gho-chliena-arifmietichieskoi-proghriessii"
    ["file_id"] => string(6) "227281"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1440675700"
  }
}

Тема урока: «Определение арифметической прогрессии, формула n-го члена».

object(ArrayObject)#875 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(133) "Тема урока: «Определение арифметической прогрессии, формула n-го члена». "
    ["seo_title"] => string(80) "tiema-uroka-opriedielieniie-arifmietichieskoi-proghriessii-formula-n-gho-chliena"
    ["file_id"] => string(6) "116612"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1412531485"
  }
}

Разработка урока по теме "Определение арифметической прогрессии"

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(121) "Разработка урока по теме "Определение арифметической прогрессии" "
    ["seo_title"] => string(73) "razrabotka-uroka-po-tiemie-opriedielieniie-arifmietichieskoi-proghriessii"
    ["file_id"] => string(6) "189144"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1426829988"
  }
}

Урок на тему "Определение арифметической прогрессии"

Просмотр содержимого документа «арифметическая прогрессия»

Определение арифметической прогрессии

Просмотр содержимого презентации «9 класс определение арифметической прогрессии»

Похожие файлы

Полезное для учителя

Просмотр содержимого документа
«арифметическая прогрессия»

Просмотр содержимого презентации
«9 класс определение арифметической прогрессии»