Тема: Разложение многочлена на множители
Цели:
- Повторить правила разложения многочлена на множители, систематизировать, расширить и углубить знания, умения обучающихся применять их при вынесении общего множителя за скобки; выявить уровень овладения учащимися комплекса знаний и умений по применению навыков умножения и деления степеней.
- способствовать развитию наблюдательности, умения анализировать, сравнивать, делать выводы; развивать навыки самоконтроля при выполнении заданий на применение правила вынесения за скобки общего множителя.
- воспитание общей культуры, активности, самостоятельности, умение общаться, воспитание объективной самооценки при оценивании знаний, работе в команде, вызывать у них потребность в обосновании своих высказываний.
Оборудование: интерактивная доска, наличие учебной презентации, задание для тестов, карточки с индивидуальными заданиями.
Тип урока: применение знаний и способов деятельности.
Ход урока:
1.Организационный момент.
Здравствуйте ребята! Сегодня на урок я пришла с хорошим настроением и хочу, чтобы у вас было такое на протяжении всего урока.( на листке изображено сердце, а на нем улыбающийся смайлик).
Девизом нашего урока станут слова И.А. Крылова:
Случается нередко нам
И труд, и мудрость видеть там,
Где стоит только догадаться
За дело просто взяться.
2. Постановка цели урока.
Учащиеся вместе с учителем формулируют тему урока с помощью опорных слов.
- Разложение многочлена на множители
- Способ группировки
- знать
- уметь
- применять
3. Актуализация знаний
Работа в группах. Стратегия «Карусель»
Задания для групп:
- Написать алгоритм разложения многочлена на множители способом вынесения общего множителя
- Написать алгоритм разложения многочлена способом группировки
- Задание на соответствие (с последующей проверкой на интерактивной доске)
Устное упражнение: вставить пропущенные выражения (слайд)
а) 18ab + 16b =...(9a + 8);
б) 4ас2 + 6а3с3- 2а2с = 2ас (.);
в) ab – ac + b2 – bc = (ab -...)+(. .. – bc) =...(b – c) + b(... – c) =...
г) 4с2 -... =... (... – 5)
4. Новый материал:
-1· (-1) = 1
а) Учитель: можно ли применить способ вынесения общего множителя за скобки в многочлену а (к+в) + с (к+в) ? Почему? Как сделать проверку? (вспомнить правило умножения двучлена на двучлен).
б) Показать прием разложения на множители выражений типа: с (а -в) +в (в -а)= с (а -в) – в (а – в )= (а – в) (с- в ). Записать на доске и в тетрадях равенства для запоминания:
а – в = - (в –а )
в) Таким образом, выносить за скобки можно не только одночлен, но и многочлен.
(с-5)2-2с(5-с)= (с-5)2-(-2с(с-5))= (с-5)2+2с(с-5)=(с-5)(с-5+2с)=(с-5)(3с-5) (решает у доски 1 ученик)
5. Закрепление, решение упражнений.
Решение заданий в группах (самопроверка)
1 группа
1) 3a + 12b
2) 2a + 2b + a2 + ab
3) 9a2 – 16а
4) 7a2 b – 14ab2 + 7ab
5) 16 – a2
6) 4a2 – 4ab + 8аb2
7) 2 (a + 5) – 3c (a + 5)
2 группа
1) 16a2 + 8ab
2) 3m – 3n + mn – n2
3) 5а-25в
4) 4a2 – 3ab + a – a
5) 5a2 – 30ab + 25аb2
6) 2 (a + b) – 3c (a + b)
7) 9a3 b – 18 ab2 – 9ab
3группа
1) 10a+15c
2) 4a2 – 18аb2
3) 6xy – ab – 2bx + 3ay
4) 7a2 + 28ab + 49ab2
5) b(a+c) + 2a + 2c
6) 5a3 c – 20acb – 10ac
7) x2 – 3x -5x + 15
На интерактивной доске показывается решение уравнения с помощью разложения на множители
1 группа
1) 3a + 12b=3(а+4b)
2) 2a + 2b + a2 + ab=2(a+b)+a(a+b)=(a+b)
(2+a)
3) 9a2 – 16а=a(9a-16)
4) 7a2 b – 14ab2 + 7ab=7ab(a-2b+1)
5) 16 a2 – 24 a=8(2a-3)
6) 4a2 – 4a b2 + 8а b=4ab(a-b+2)
7) 2 (a + 5) – 3c (a + 5)=(a+5)(2-3c)
2 группа
1) 16a2 + 8ab=8a(2a+b)
2) 3m – n2 + mn – 3n=(3m-3n)+(mn-n2)=3(m-n)+n(m-n)=(m-n)(3+n)
3) 5а-25в=5(a-5b)
4) 4a2 – 3ab + a – a=a(4a-3b)
5) 5a2 – 30ab + 25аb2=5a(a-6b+5b2)
6) 2 (a + b) – 3c (a + b)=(a+b)(2-3c)
7) 9a3 b – 18 ab2 – 9ab=9ab(a2-2b-1)
3группа
1) 10a+15c=5(2a+3c)
2) 4a2 – 18аb2=2a(2a-9b2)
3) 6xy – ab – 2bx + 3ay=(6xy+3ay)-(ab+2bx)=3y(2x+a)-b(a+2x)=(2x+a)(3y-b)
4) 7a2 + 28ab + 49ab2=
7a(a+4b+7b2)
5) b(a+c) + 2a + 2c= b(a+c) +2(a+c)=(a+c)(b+2)
6) 5a3 c – 20acb – 10ac=
5ac(a2-4b-2)
7) x2 – 3x -5x + 15=( x2 – 3x)-(5x-15)=x(x-3)-5(x-3)=(x-3)(x-5)
6. Работа в группах
1 группа №143 (1,2)
2группа №143 (3,4)
3 группа №143 (5,6)
Проверка – запись у доски от каждой группы по 1 человеку.
7. Самостоятельная работа с последующей взаимопроверкой
I вариант II вариант
3х(1-9х)=0 4х(1-5х)=0
3х=0 1-9х=0 4х=0 1-5х=0
Х=0 9х=1 х=0 5х=1
х=1/9 х=1/5
3 ученика работают индивидуально по карточкам.
1карточка. Решите уравнение:.
2 карточка. Решите уравнение:.
3 карточка. Решите уравнение:.
8. Тестовая работа в двух вариантах с последующей взаимопроверкой.
I вариант
1. Упростите выражение:.
1) ; 2)8х; 3) 8х-3; 4) -8х-3.
2. Вынесите общий множитель за скобки:.
1) ; 2) ; 3) ; 4)
3.Представьте выражение в виде произведения двух многочленов: (у-5) х – 3(у-5)
1) (у-5)(х-3); 2) (5-у)(х-3); 3) (у-5)(1-х); 4) (3-х)(у-5).
4.Найдите корни уравнения:.
1) 1; 2) корней нет; 3) -1;0; 4) 0;1.
5. Известно, что Вычислите
1) 11; 2) 4; 3) 10; 4) -4.
II вариант
1. Упростите выражение:.
1) -15; 2)15; 3) ; 4).
2. Вынесите общий множитель за скобки:.
1) ; 2) ; 3) ; 4)
3.Представьте выражение в виде произведения двух многочленов: (3+у) х – 4(3+у)
1) (3+у)(х+4); 2) (х-4)(3+у); 3) (у+3)(4-х); 4) (3-у)(х-4).
4.Найдите корни уравнения:.
1) 0; 2) корней нет; 3) -1;0; 4) 0;1.
5. Известно, что Вычислите
1) 11; 2) 15; 3) 10; 4) -4.
На интерактивной доске появляется таблица верных ответов к тестам:
№ задания
1
2
3
4
5
I вариант
3
2
1
4
3
II вариант
1
3
2
3
2
9. Подведение итогов урока.
На вертикальной прямой отметьте снежинкой.
· Кто может самостоятельно применять изученные способы разложения многочлена на множители при решении уравнений? (Снежинка вверху на прямой).
· Кому нужна помощь? (Снежинка внизу на прямой).
Оценочный лист _________________________________________
№
Задание
Оценка
Своя оценка
Оценка командира группы
1
Решение заданий в группе
7 – «5»
5,6 – «4»
4 – «3»
0,2 – «2»
2
Работа в группах
решение №143
3
Самостоятельная работа
4
Тест (взаимопроверка)
5 – «5»
4 – «4»
3 – «3»
0,2 – «2»
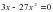
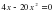
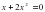 .
.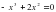 .
.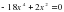 .
.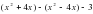 .
.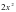 ; 2)8х; 3) 8х-3; 4) -8х-3.
; 2)8х; 3) 8х-3; 4) -8х-3.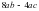 .
.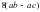 ; 2)
; 2) 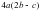 ; 3)
; 3) 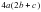 ; 4)
; 4) 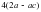
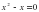 .
.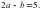 Вычислите
Вычислите 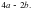
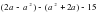 .
.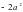 -15; 2)15; 3)
-15; 2)15; 3) 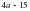 ; 4)
; 4) 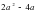 .
.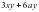 .
.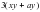 ; 2)
; 2) 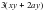 ; 3)
; 3) 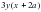 ; 4)
; 4) 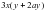
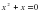 .
.