В работе представлена технологическая карта, презентация урока по теме "Решение задач на проценты" для учащихся 8 класса. Карта составлена в соответствии с рабочей программой, календарно-тематическим планом и соответствует требованиям стандартов нового поколения. УМК, составляющей частью которго является технологическая карта урока по математике, имеет дидактическое и методическое оснащение, что обеспечивает эффективность реализации образовательной, развивающей, воспитательной целей урока. В данной работе отражено использование на уроках современных педагогических технологий: практико-деятельностные, игровые технологии. Карта и презентация урока рекомендованы к использованию в учебном процессе учителям математики.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
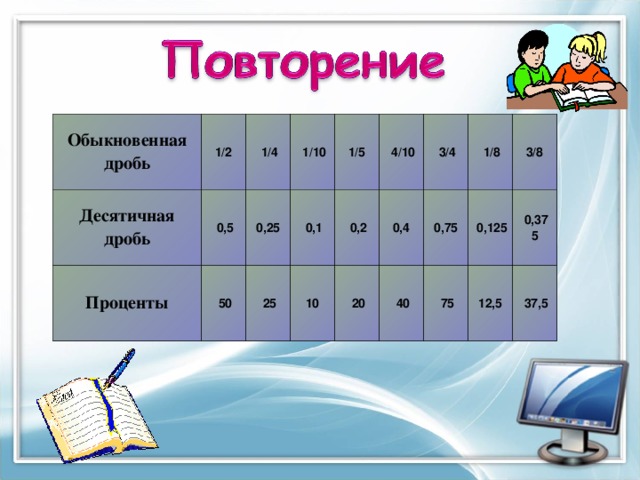
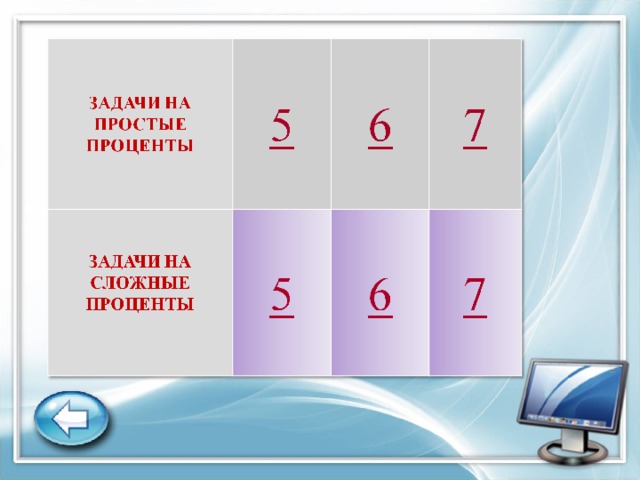
Технологическая карта урока "Решение задач на проценты" 8 класс
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Технологическая карта урока "Решение задач на проценты" 8 класс »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2000 руб.
2860 руб.
2100 руб.
3000 руб.
2220 руб.
3170 руб.
1230 руб.
1760 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства