| Этап урока | Деятельность учителя | Деятельность ученика | Задачи для учащихся, выполнение которых приведёт к достижению запланированных результатов
| Планируемые результаты |
| 1. Организа-ционный этап (1 мин.) | Приветствует учащихся, проверяет готовность учащихся к уроку. Психологический настрой учащихся.
| Учащиеся проверяют подготовку к занятию, записывают в тетрадях число «Классная работа»,. Настраиваются на деловой ритм работы. | Ребята, наш урок будет проходить под девизом: «Если будешь дроби знать, Точно смысл их понимать, Станет легкой даже трудная задача».
| Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. Регулятивные: организация своей учебной деятельности Учащиеся концентрируют внимание, включаются в деловой ритм урока. |
| 2. Целеполагание и мотивация к учебной деятельности. (1 мин.)
| Устанавливает тематические рамки. Создаёт условия для осознания учащимися целей урока. | Слушают учителя, участвуют в беседе, способствующей постановке учебной проблемы и формулированию темы урока. | -Какую тему вы изучили на прошлом уроке? -Сегодня мы продолжим работу с дробями. Ведь, чтобы новых знаний набраться, нужно на старые опираться!
| Коммуникативные: умение осознанно и произвольно строить речевое высказывание в устной форме; умение вступать в диалог, участвовать в коллективном обсуждении вопроса. Регулятивные: целеполагание, умение самостоятельно определять цель своей учебной деятельности. Личностные: мотивация учения |
| 3. Актуализация опорных знаний учащихся. (4 мин.) | Организует фронтальную работу с классом для актуализации имеющихся знаний и умений, создаёт проблемной ситуацию, способствующую формулированию учащимися определений правильной и неправильной дробей. | Отвечают на вопросы учителя.
Выполняют задание. Работа в парах
Ответ: 1) натуральные числа обозначают целые единицы, а дробные – части единиц 2) черта означает знак деления 3) Среди них есть правильные и неправильные. 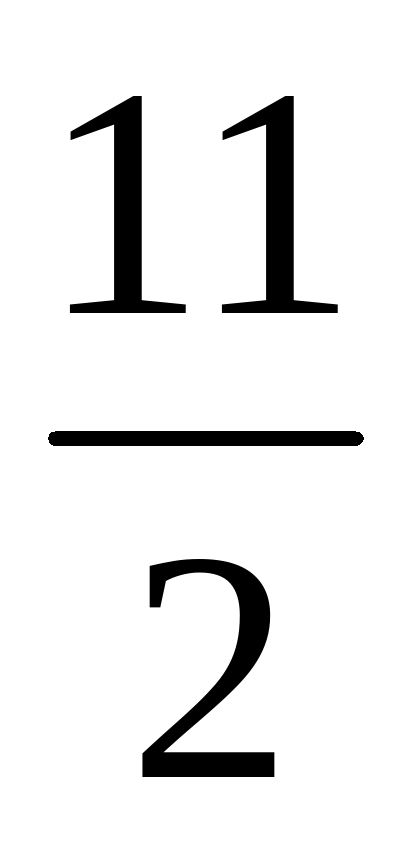 ; ; 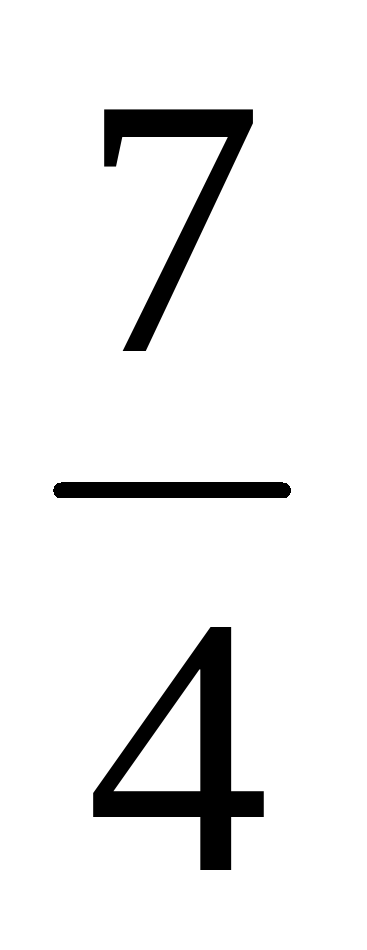 . .
| Разбейте числа на 2 группы I - натуральные числа; II - дробные числа
36; 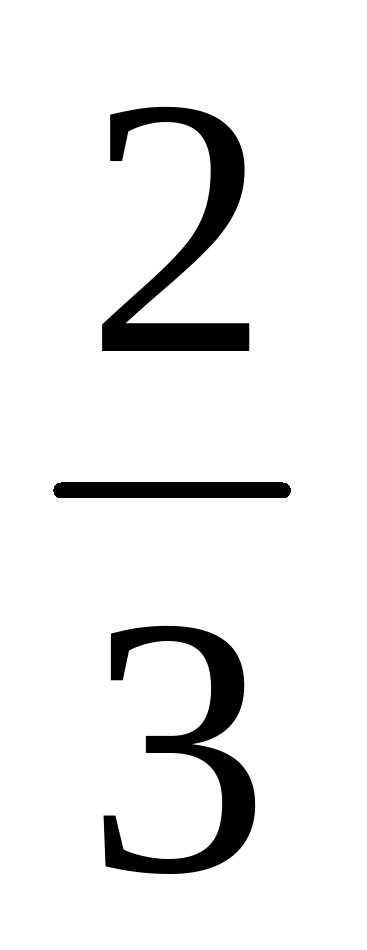 ; ; 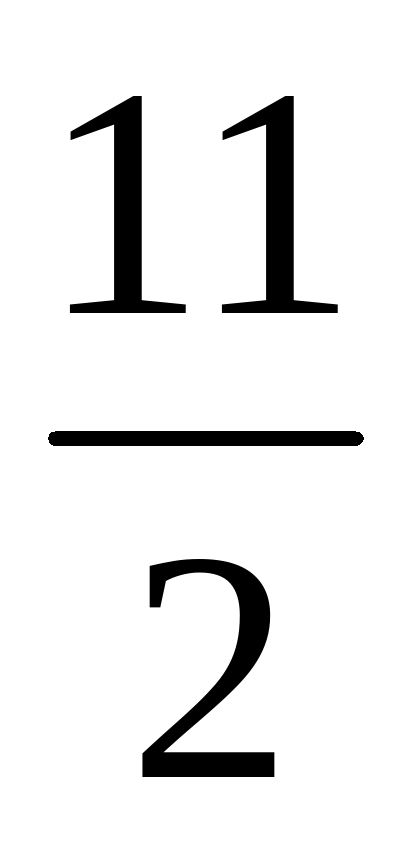 ; 6; ; 6; 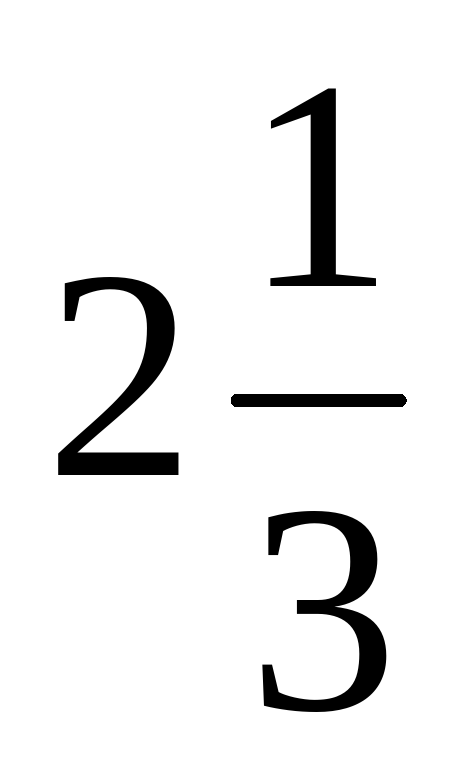 ; ; 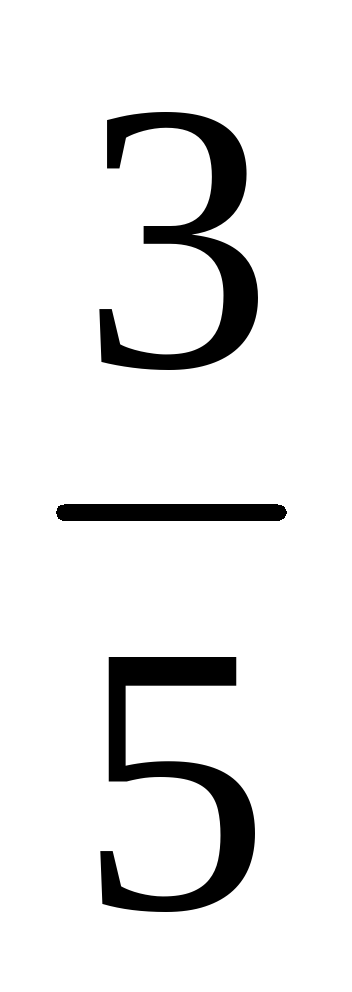 ; 12; 5; ; 12; 5; 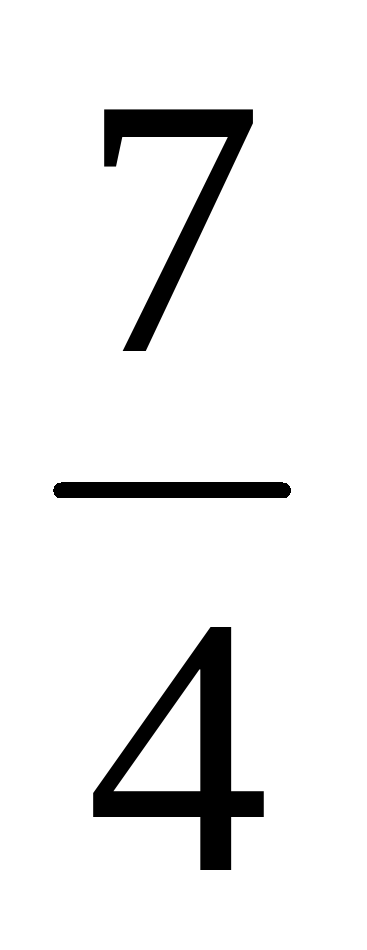 . .
1) Чем натуральные числа отличаются от дробных? Что они обозначают?
2) Что означает черта в дроби? (деление)
- Взаимопроверка ОЦЕНКА (+), (--)
3) Во второй группе вы записали дроби, чем они отличаются? 3) Назовите неправильные дроби.
| Познавательные: структурирование собственных знаний. Коммуникативные: умение выражать свои мысли с достаточной точностью. Регулятивные: контроль и оценка процесса и результатов деятельности.
|
| 4. Формирование новых знаний. (8 мин.) | Обеспечение восприятия, осмысления и первичного запоминания детьми изучаемой темы: определения смешанного числа Организует работу с учебником. Организует фиксирование нового знания в речи и знаках | Отвечают на вопросы учителя, обмениваются мнениями, выполняют записи в тетради. Записывают в тетрадях тему урока.
Работа с учебником.
Смешанными числами называются числа, состоящие из целой и дробной части Записывают в тетрадях. | . Проблемная ситуация - К какой группе можно отнести число 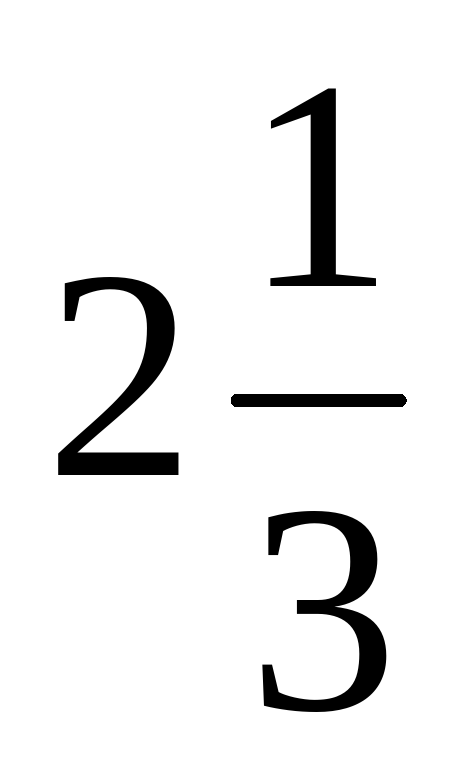 ? ? - Что заметили нового, интересного?
Проблемная ситуация -А мы знаем как такие числа называются? -Какое же название вы могли дать этому числу? Правильно, ребята такие числа называются –смешанными. -Тогда как мы назовем тему нашего урока? Запишем в тетради тему урока «Смешанные числа»
Откройте учебник на странице 194, прочитайте приведенные там определения.
| Личностные: ответственно относиться к учению; проявлять инициативу при выполнении заданий; Познавательные: анализируя и сравнивая задания, извлекают необходимую информацию для открытия нового понятия. Коммуникативные: умение выражать свои мысли с достаточной точностью. Регулятивные: контроль и оценка процесса и результатов деятельности. |
| 6. Первичное закрепление изученного (15 мин.) | Организует усвоение нового знания. Организует работу по выполнению упражнений с проговариванием во внешней речи. Осуществляет контроль за процессом решения задач |
Работают в парах.
| Запись смешанных чисел (Учитель объясняет это на доске) 1)�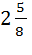 �(дробная черта по середине целой части) �(дробная черта по середине целой части) 2 – целая часть � �- дробная часть Пример: �- дробная часть Пример: 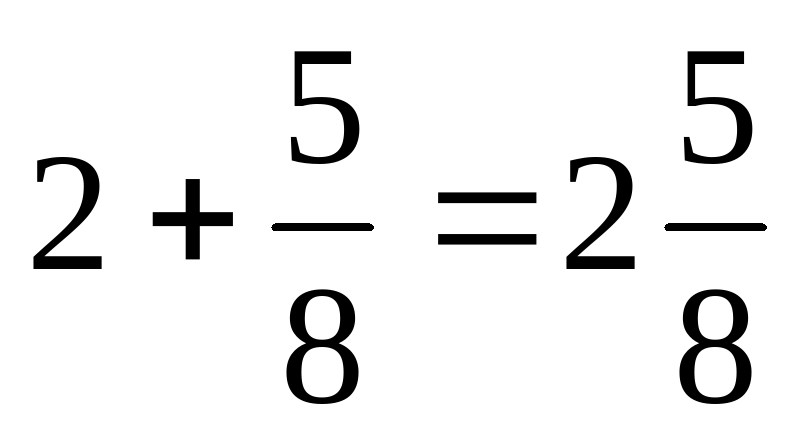 (принято записывать короче) (принято записывать короче) Обратите внимание! Дробная часть смешанного числа---правильная дробь.
2) Приведите свой пример по одному смешанному числу, прочитайте соседу и пусть он его запишет. Запишите своё число: целая часть пусть будет
дата твоего дня рождения, а в дробной части числитель – порядковый номер месяца (2), а знаменатель – сегодняшнее число (16). Взаимопроверка ОЦЕНКА (+), (--)
Перевод из неправильной дроби в смешанное число А встречались ли нам с вами неправильные дроби в начале урока? А как вы думаете, что с ними можно сделать? Чему мы должны научиться? Представим неправильную дробь 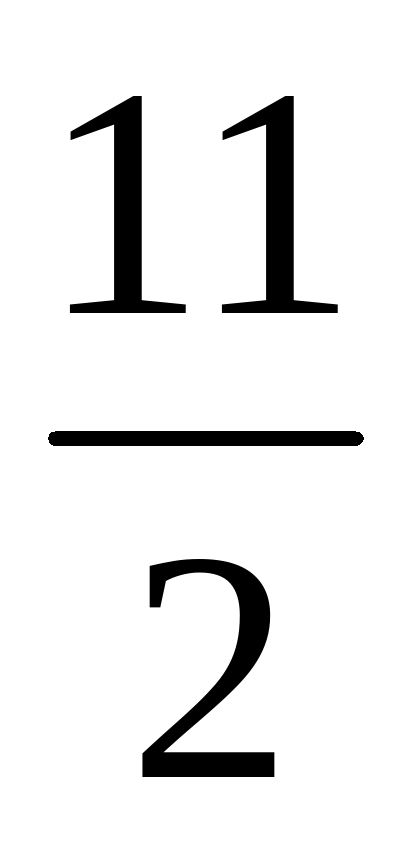 �� в виде смешанного числа �� в виде смешанного числа Что предлагаете?
Делить столбиком. А как? К чему мы можем обратиться для уточнения своих предположений? На стр. 195 показан способ выделения целой части из неправильной дроби, рассмотрите и выделите целую часть из �� . 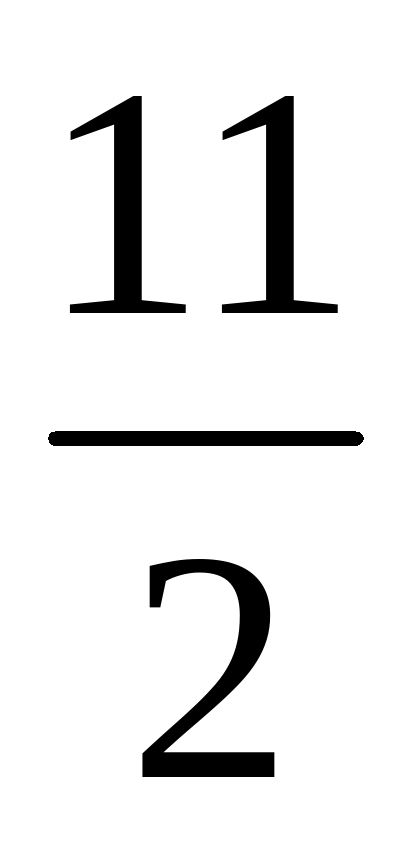
| Личностные: развитие самооценки Познавательные: совершенствование умения осуществлять сравнение, выявлять объект, подходящий под данное определение. Коммуникативные: уметь оформлять свои мысли в устной форме; слушать и понимать речь других. Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата. |
| 5. Физкульт.минутка (1 мин.)
| Организовать смену деятельности, обеспечить эмоциональную разгрузку учащихся
| Учащиеся сменили вид деятельности и готовы продолжить работу
| А теперь, ребята встали. Быстро руки вверх подняли, В стороны, вперед, назад. Повернулись вправо, влево, Тихо сели, вновь за дело.
|
|
| 7. Контроль и коррекция знаний (8 мин.)
| Организует самостоятельную работу по закреплению изученного с последующей проверкой. Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок. Организует работу в парах. Контролирует деятельность учащихся, при необходимости консультирует в появившихся вопросах.
| Учатся применять полученные знания в процессе индивидуальной работы. Учащиеся анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность решения задач.
Работают в парах
| Задача № Как разделить поровну 6 апельсинов на 5 детей? Сколько апельсинов получит каждый ребёнок?
Работают индивидуально. Проверяем ответы по слайдам. Взаимопроверка в парах ОЦЕНКА (+), (--) Самостоятельная работа. Выполняют задания. Проверяют правильность выполнения по образцу. (кейс) Взаимопроверка в парах ОЦЕНКА (+), (--)
Предлагает выполнить совместно задания с УМК №769, №771, № 773, №775
(Самостоятельно и у доски)
САМООЦЕНКА (+), (--)
Парная работа. В предложенных вариантах ОГЭ 9 класса найти задания на действия со смешанными числами! -Знания, полученные на уроках математики вам необходимы при сдачи ОГЭ в 9 классе.
| Личностные: формирование позитивной самооценки Коммуникативные: умение работать в парах, группах, уважительно относиться к мнению других Регулятивные: умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы;осуществлять навыки взаимоконтроля в ситуации общения
|
| 8. Рефлексия учебной деятельности (5 мин.) | Организует фиксирование нового содержания, самооценку учебной деятельности. Предлагает оценить свою деятельность с помощью смайла. | Отвечают на вопросы, рассказывают, что узнали, смогли выполнить. Оценивают свою учебную деятельность | Что вы нового узнали на уроке? Чему вы научились на уроке? - Оцените свою деятельность на уроке и настроение, используя один из кружочков: -Я все понял и мне было интересно -Я понял на уроке, но у меня есть вопросы -Я ничего не понял на уроке, мне было скучно (выставление оценок) 6-7 «+» оценка 5 4-5 «+» оценка 4 3 «+» оценка 3 0-2 «+» оценка 2 | Личностные: проводят самооценку, учатся адекватно принимать причину успеха ( неуспеха) Регулятивные: оценивание собственной деятельности на уроке
|
| 9. Информация о домашнем задании (2 мин.) | Обеспечивает понимание детьми содержания и способов выполнения домашнего задания. Дает комментарий к домашнему заданию | Учащиеся записывают в дневники задание | § 29, стр. 194-195, выучить определения;
| Личностные: ответственное отношение к учению |
















