Тема. Свойства равнобедренного треугольника.
Цель: повторить понятия медианы, высоты и биссектрисы треугольника, научить применять свойства равнобедренного треугольника при решении задач.
Ход урока.
- Орг. момент.
- Проверка домашней работы (№ 114, 115).
- Устная работа.
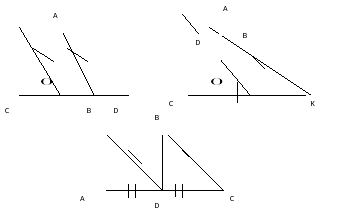
На кодоскопе задание: Найти угол DBA.
- Устный опрос.
- Какой отрезок называется медианой треугольника?
- Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник?
- Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?
- Какой треугольник называется равнобедренным? Как называются его стороны?
- Какой треугольник называется равносторонним?
- Сформулировать теорему об углах равнобедренного треугольника.
- Сформулировать теорему о биссектрисе равнобедренного треугольника
- Решение задач.
№ 115
Решение:
Дано: АВ=ВС, CD=DE.
Доказать:ВАС=CED.
Доказательство: (по рисунку 67 учебника.).АВС и CDE равнобедренные по условию, значит A=ACB=DCE=E (по свойству углов равнобедренного треугольника).
№118
Дано: АВС, АВ=АС, МВС, NBC, MB=CN
Доказать: ВАМ=CAN.
Доказательство: а) В=С( по свойству углов при основании равнобедренного треугольника), АВ=АС, ВМ=NC ( по условию). Следовательно АВМ=ANC.
б) Так как ABM=ANC, значит MA=NA. Поэтому AMN-равнобедренный.
№ 159 (резерв).
- Домашнее задание. § 2, № 119, 120.
- Итог урока, выставление оценок.
 ВАС=
ВАС=
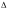 АВС и
АВС и  ВС, N
ВС, N















