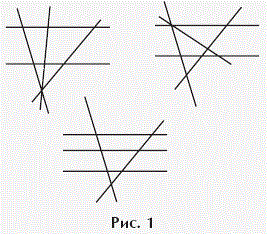
Нарисуйте на плоскости пять различных прямых так, чтобы они пересекались ровно в семи различных точках.
Решение :
Три возможных ответа изображены на рисунке 1. Можно показать, что других конфигураций из пяти прямых, пересекающихся ровно в семи различных точках, нет.
Задача № 2 :
Мальчик пошел с отцом в тир. Отец купил ему 10 пулек. В дальнейшем отец за каждый промах отбирал у сына одну пульку, а за каждое попадание давал одну дополнительную пульку. Сын выстрелил 55 раз, после чего пульки у него кончились. Сколько раз он попал?
Ответ: 50.
Решение :
Каждый раз, когда мальчик попадал в цель, число имеющихся у него пулек оставалось прежним (одну использовал и одну получил от отца). Каждый раз, когда мальчик промахивался, число имеющихся у него пулек уменьшалось на 2 (одну использовал и одну отобрал отец). Это значит, что сын за 55 выстрелов промахнулся 10 : 2 = 5 раз, стало быть, попал 55 – 5 = 50 раз.
Задача № 3 :
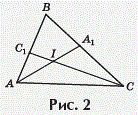
Две биссектрисы треугольника пересекаются под углом 60°. Докажите, что один из углов этого треугольника равен 60°.
Решение :
Пусть биссектрисы AA1 и CC1 треугольника ABC пересекаются в точке I (рис.2). Допустим, что AIC1 = 60°. По теореме о внешнем угле треугольника
откуда
BAC + BCA = 120°
и
ABC = 180°– BAC – BCA = 60°.
Но это еще не все решение: ведь может случиться, что AIC = 60°. Однако тогда
IAC + ICA = 120°,
откуда
BAC + BCA = 240°,
что невозможно.
AIC1 = 60°. По теореме о внешнем угле треугольника
