ПрактическАЯ РАБОТА№ 9
Тема: Решение задач на концентрацию
Цели:
- изучить алгоритм решения задач на концентрацию
Оснащение занятия: конспект лекций.
Порядок выполнения работы
Задание 1.
- Ознакомиться с лекцией № 7
- Выписать в тетрадь алгоритмы решения задач на концентрацию
- Записать в тетрадь решение рассмотренных задач
Задание 2.
Решить задачи для самостоятельного решения
Лекция 7.
Тема «Решение задач на концентрацию»
В задачах этого типа основным является понятие «концентрация». Что же это такое?
Рассмотрим, например, раствор кислоты в воде. Пусть в сосуде содержится 10 литров раствора, который состоит из 3 литров кислоты и 7 литров воды. Тогда относительное (по отношению ко всему объему) содержание кислоты в растворе равно . Это число и определяет концентрацию кислоты в растворе. Иногда говорят о процентном содержании кислоты в растворе. В приведенном примере процентное содержание будет таково: . Как видно, переход от концентрации к процентному содержанию и наоборот весьма прост.
Итак, пусть смесь массы М содержит некоторое вещество массой m. Тогда:
- концентрацией данного вещества в смеси (сплаве) называется величина ;
- процентным содержанием данного вещества называется величина с×100%;
Из последней формулы следует, что при известных величинах концентрации вещества и общей массы смеси (сплава) масса данного вещества определяется по формуле m=c×M.
Задачи на смеси (сплавы) можно разделить на два вида:
- Задаются, например, две смеси (сплава) с массами m1 и m2 и с концентрациями в них некоторого вещества, равными соответственно с1 и с2. Смеси (сплавы) сливают (сплавляют). Требуется определить массу этого вещества в новой смеси (сплаве) и его новую концентрацию. Ясно, что в новой смеси (сплаве) масса данного вещества равна c1m1+c2m2, а концентрация .
- Задается некоторый объем смеси (сплава) и от этого объема начинают отливать (убирать) определенное количество смеси (сплава), а затем доливать (добавлять) такое же или другое количество смеси (сплава) с такой же концентрацией данного вещества или с другой концентрацией. Эта операция проводится несколько раз.
При решении таких задач необходимо установить контроль за количеством данного вещества и его концентрацией при каждом отливе, а также при каждом доливе смеси. В результате такого контроля получаем разрешающее уравнение. Рассмотрим конкретные задачи.
Задача 1. Имеется кусок сплава меди с оловом общей массой 12 кг, содержащий 45% меди. Сколько чистого олова надо добавить к этому куску сплава, чтобы получившийся новый сплав содержал 40% меди?
Решение:
Пусть хкг олова надо добавить к сплаву. Так как процентное содержание меди в сплаве равно 45 %, то масса меди в первоначальном сплаве m=0,45×12=5,4 кг (где 0,45 – концентрация меди в сплаве).
Тогда 12+х– масса нового сплава
И так как масса меди в первоначальном сплаве равна 5,4 кг, то
– концентрация меди в новом сплаве.
По условию , решая уравнение, получаем х=1,5 кг.
Ответ: нужно добавить 1,5 кг чистого олова.
Задача 2. Имеются два раствора кислоты разной концентрации. Объем одного раствора 4 л, другого – 6 л. Если их слить вместе, то получится 35 % раствор кислоты. Если же слить равные объемы этих растворов, то получится 36 % раствор кислоты. Сколько литров кислоты содержится в каждом из первоначальных растворов?
Решение:
Пусть хл кислоты содержится в первом растворе,
ул кислоты содержится во втором растворе.
Тогда – концентрация кислоты в первом растворе,
– концентрации кислоты во втором растворе.
Если слить два раствора, то получим раствор массой 4л+6л=10л, причем масса кислоты в нем будет х+у, тогда
– концентрация кислоты, после сливания обоих растворов.
Так как по условию в полученном таким образом растворе содержится 35% кислоты, то ее концентрация там равна 0,35.
Таким образом, получаем: или х+у=3,5.
Если будем сливать равные объемы растворов по m литров, то
– масса кислоты в полученном растворе,
2m – масса полученного раствора,
тогда
– концентрация кислоты в полученном растворе.
По условию
или .
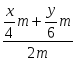 – концентрация кислоты в полученном растворе.
– концентрация кислоты в полученном растворе.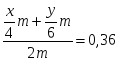 или
или 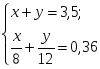 Þ
Þ















