Интегрированный урок математика и химия «Решение задач на растворы и сплавы» 11 класс

Данные об авторе

Автор(ы): 

Толыбаева Айша Кучербаевна-учитель математики

Нечай Оксана Леонидовна-учитель химии

Место работы, должность: 

 Школа-гимназия № 22город Астана

Класс(ы): 

11 класс

Предмет(ы): 

 Алгебра

 Математика

 Химия

Тема урока: «Решение задач на растворы и сплавы»

Цель урока: учащиеся будут применять приемы решения текстовых задач на растворы и сплавы.

Цель урока:  Рассмотреть различные типы задач на растворы и приемы их решения.

образовательные:

• познакомиться с приемами решения задач в математике и химии;

• сформировать целостную картину о взаимосвязи предметов в школе;

Воспитательные задачи: совершенствовать интеллектуальные умения (анализ, прогнозирование, умения устанавливать причинно-следственные связи)

Задачи развития учащихся: продолжить формирование ценностного отношения к исследовательской деятельности как основному способу получения знаний в химии; создать условия для развития умений наблюдать и объяснять химические явления, умений анализировать результаты наблюдаемых опытов, грамотного химического языка, коммуникативных умений, самостоятельности в мышлении и учебной работе; формирование навыков самоконтроля и самооценки, навыков работы с реактивами.

Технологии:

Традиционные – проблемно-поисковый метод, выполнение эксперимента, работа с инструкционной картой.

Инновационные – ИКТ.

развивающие:

• формировать умения учащихся анализировать, сравнивать, обобщать, углублять и делать самостоятельные выводы с помощью вопросов и заданий;

• продолжить развитие мыслительных способностей учащихся; развивать умение работать в группе;

воспитательные:

• продолжить формирование здорового образа жизни;

• воспитывать творческую, гармонично развитую личность, формировать у учащихся коммуникативные навыки.

Тип урока: 

 Комбинированный урок

Краткое описание: 

 Интегрированный урок математика + химия на тему: «Решение задач на сплавы растворы»

                     

Ход урока.

                                       Организационный момент.

 

Учитель математики: Сегодня у нас необычный урок, это интегрированный урок математики и химии и вести его будут два учителя. На этом уроке мы посмотрим с вами на задачи с двух точек зрения – с химической и математической, и выясним: как математика помогает в решении химических задач и как химия решает некоторые математические задачи.

Учитель химии: Здравствуйте, ребята! Мы с вами увидим, как применить математические методы при решении задач по химии.

Тема урока: Решение задач на растворы и сплавы.

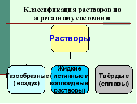
Учитель химии: Какие бывают растворы?

Ответ: Жидкие, твердые, газообразные по агрегатному состоянию. Насыщенные и ненасыщенные по растворимости веществ в воде. Истинные и коллоидные по размеру частиц.

Учитель химии: как выражают концентрацию раствора?

Какие существуют способы выражения концентрации растворов?

Ответ: массовая доля (w) и молярная концентрация раствора (См). Дать определения.

Ученик: w, mр.в., См, mр-ра, nр.в., Vр-ра

Учитель математики: А с математической точки зрения - разное процентное содержание вещества.

Итак, тема урока  « Решение задач на сплавы и растворы».

 

Цель урока:  Рассмотреть алгоритм решения задач на растворы, познакомить с приемами решения задач в математике и химии, расширить знания  о значении этих растворов в быту, сформировать целостную картину о взаимосвязи предметов в школе.

Девиз: «Только из союза двух работающих вместе и при помощи друг друга рождаются великие вещи»                                   Антуан де Сент- Экзюпери

Учитель математики: Для урока необходимо повторить понятие процента.

1 этап. Актуализация понятия процента.

Математическая разминка (проводит учитель математики).

Математическая разминка (проводит учитель математики).

Вспомним проценты: - Что называют процентом? (1/100 часть числа.)

- Выразите в виде десятичной дроби 17%, 40%, 6%

- Выразите в виде обыкновенной дроби 25%, 30%, 7%

- Установите соответствие 40%         1/4

                                                  25%        0,04

                                                  80%        0,4

                                                  4%          4/5

Как найти % от числа? (% записать в виде дроби, умножить число на эту дробь.)

 

- Найти 10% от 30 (10%=0,1    30*0,1=3)

- Вычислите 1) 20% от 70       2) 6% от 20               

                        3) х% от 7 

1. Найти 30% от 2430 (729)

2. Сколько % составит 12 от 60? (20%)

3. Найдите число, 20% которого равны 42 (210)

4. Какое число, увеличенное на 11% составит 222? (200)

5. На сколько % число 180 больше числа 108? (40%)

6. На сколько % число 120 меньше числа 150? (20%)

7. В бронзе – сплаве меди с оловом, на долю олова приходится 20%. Сколько весит олово, пошедшее на создание Медного всадника, если масса памятника 5 тонн? (1 тонна)

8. Найти массу 25% раствора, в котором растворено 80 г вещества. (320 г)

9. Какова массовая доля раствора, при выпаривании 300 г которого получено 30 г соли? (10%)

10. Рассчитать массовую долю раствора, полученного растворением 20 кг щелочи в 80 кг воды. (20%)

Цель: учащиеся будут демонстрировать навыки решения расчетных задач. На 5минут предложено решить 5 задач из сборника тестов для подготовки к ЕНТ.

2 этап. Проверка домашнего задания. Бенефис одной задачи.

Цель: на данном этапе урока учащиеся демонстрируют оригинальные способы решения задач, полученных предварительно на дом.

1 группа.

Сплав алюминия и цинка содержит 82% алюминия. После добавления 18кг цинка содержание алюминия в сплаве понизилось до 70%. Вычислите, сколько алюминия и цинка в отдельности содержится в сплаве.

Ответ: 81,6кг. 36,9кг

2 группа.

Сплав состоит из меди и цинка. В первом куске меди содержится 60% и цинка 40%, а во втором это соотношение равно 7:3 Сколько следует взять от каждого куска, чтобы получить 1кг нового сплава, в котором медь и цинк находились бы в соотношении 11:5?

Ответ: 125г 875г

3группа.

Два слитка состоят из меди, цинка и олова. В первом слитке 40% олова, во втором 26% меди. Процентное содержание цинка в первом и во втором слитке одинаковое. Сплавив 150г первого и 250г второго, получили новый сплав, в котором оказалось 30% цинка. Сколько граммов олова содержится в новом сплаве.

Ответ: 170г

4 группа.

В одной тонне руды содержится определенное количество железа. После удаления из руды 400кг примесей, содержащих 12,5% железа, в оставшейся руде содержание железа повысилось на 20%. Какое количество железа осталось в руде?

Ответ: 375кг

3 этап урока. Методы решения задач на растворы и сплавы.

Учащиеся работаю в 4 группах.

Предложены задачи, встречающиеся в ЕНТ. Смотрите приложение №1.

Учитель: Итак, сегодня на уроке мы познакомились ещё с одним способом решения задач на смешивание растворов. Я хотела бы услышать от вас ответ на следующие вопросы: 
1. Нужен ли нам данный способ и что в нём замечательного? 
2. А нужен ли нам алгебраический способ? 
После того, как учитель выслушал ответы учеников, делает вывод: 
-Алгебраический способ решения задач на смешивание растворов учит детей строить цепочку логических рассуждений. «Конверт Пирсона»-это механический способ, который позволяет рационально и экономно проводить вычисления при решении задач по алгебре на ЕНТ. Поэтому, зная, два способа решения задач на растворы, один из них всегда можно применить в нужной ситуации. 

Практическая работа: «Приготовление раствора заданной концентрации».

Первой группе учащихся было предложено задание: приготовить 250мл 3% раствора глюкозы из 5% раствора глюкозы.

Оборудование: калькулятор, пипетка на 10мл, мерный цилиндр, колба с дистиллированной водой, раствор глюкозы 5%.

Этапы практической работы:

1. Постановка вопроса, обусловливающего цель работы.

2. Инструктаж технический и организационный.

3. Выполнение работы (определение, наблюдение, постановка опыта).

4. Фиксация результатов (проводится одновременно с выполнением работы).

5. Выводы, отвечающие на поставленный вопрос.

Отчет учащихся:

Было получено задание: приготовить 250мл 3% раствора глюкозы из 5% раствора глюкозы. Плотность растворов глюкозы считаем равной 1г\мл.

Проведены расчеты по формуле массовая доля вещества – это отношение массы вещества к массе раствора. Найдена масса 250мл раствора по плотности. Найдена масса вещества в 250г 3% раствора. Рассчитана масса 5% раствора глюкозы – 150г.

С помощью мерного цилиндра отмерили 150мл раствора глюкозы (плотность равно 1г\мл). В колбу для приготовления растворов на 250мл через воронку прилили 150мл раствора глюкозы и довели объем до метки. Использовали дистиллированную воду.

Результат: получен 3% раствор.

Было получено задание: в пипетку на 10 мл набрать 40% раствор глюкозы. Приготовить раствор в колбе на 500 мл. Рассчитать концентрацию полученного раствора.

Проведен расчет. В 10мл раствора масса глюкозы составляет 4г. Масса раствора 500г (учитываем, что плотность раствора глюкозы 1г\мл. Концентрация глюкозы 0,8%.

Было получено задание: в пипетку на 10 мл набрать 40% раствор глюкозы. Приготовить раствор в колбе на 250 мл. Рассчитать концентрацию полученного раствора.

Проведен расчет. В 10мл раствора масса глюкозы составляет 4г. Масса раствора 250г (учитываем, что плотность раствора глюкозы 1г\мл. Концентрация глюкозы 1,6%.

Было получено задание: приготовить 15% раствор из 5% и 40%.

Используем конверт Пирсона для расчета частей растворов. Растворы смешиваем в соотношении 5:2. В пипетку наберем 10мл 40% раствора и отмерим 25мл 5% раствора. При смешивании получим 35мл 15% раствора.

Группа 2. Определение массовой доли редуцирующих веществ методом Лейна – Эйлона

Цель: установить концентрацию раствора глюкозы с помощью метода Лейна-Эйлона.

Фактором раствора Фелинга называют число, соответствующее объему в куб.см раствора глюкозы, затраченному на титрование 25см смеси растворов Фелинга.

Предварительное титрование

В плоскодонную колбу вместимостью на 100 см куб. пипеткой вносят 25 см куб. смеси растворов Фелинга, перемешивают на магнитной мешалке или вручную. Смесь доводят до кипения на электрической плитке, кипятят 2мин и из бюретки вносят стандартный раствор глюкозы. Снова нагревают колбу, раствор кипятят 2мин, затем добавляют 2-4 капли метиленовой сини, а из бюретки дотитровывают, по каплям до перехода окраски индикатора из синей в бесцветную. Отмечают объем, пошедший на титрование. Титрование проводят 3 раза, вычисляют среднее арифметическое. Это число является фактором раствора Фелинга.

Приготовление растворов ( вы используете готовые растворы )

Раствор Фелинга 1.

В стеклянном стакане взвешивают навеску сернокислой меди массой 34,64г, растворяют в дистиллированной воде и переносят в колбу на 500 см куб. перемешивают раствор при температуре 20 градусов доводят дистиллированной водой до метки. Раствор Фелинга 1 хранят в стеклянном флаконе не более 6 месяцев.

Раствор Фелинга II

В стеклянном стакане взвешивают навеску виннокислого калия-натрия массой 173г и растворяют в дистиллированной воде. Также взвешивают навеску гидроокиси натрия массой 50г и отдельно растворяют в 100мл дистиллированной воды. Оба раствора переносят в мерную колбу вместимостью 500мл температуре 20 градусов доводят дистиллированной водой до метки. Раствор Фелинга II хранят в стеклянном флаконе не более 3 месяцев.

Смесь растворов Фелинга I и Фелинга II ( на уроке нужно их приготовить с помощью пипетки на 10мл В пипетку набираете растворы грушей)

Растворы соединяют в соотношении 1:1 и тщательно перемешивают. Смесь хранят в полимерном флаконе не более 1 недели.

Группа 3. Определение глюкозы с помощью глюкометра «GAMMA».

Вставьте тест полоску в приемник глюкометра лицевой стороной вверх и контактами вперед. Контакты должны полностью пройти, чтобы результат был точным. Прибор включается автоматически, на дисплее появляется символ капли крови. Каплю объемом 0,5 микролитра исследуемого раствора глюкозы нанесем на предметное стекло и поднесем к ней абсорбирующий участок на тест полоске. (Не трите тест полоску пальцами и не используйте загрязненные тест полоски). Жидкость должна полностью заполнить контрольное окошко перед тем как глюкометр начнет отсчет. Результаты измерений появляются на дисплее после того, как глюкометр закончит отсчет.

Диапазон измерений: 1,1-33,3 ммоль\литр

Группа 4. Разработка рецептуры коктейла.

Цель: разработать рецептуру коктейля.

Для приготовления коктейла мы использовании пломбир классический торговой марки «Золотой стандарт», жирность 15% и молоко жирность 6%.

Расчет: если смешать молоко и мороженое в соотношении 1:1, то получится коктейл жирностью 28%.

В блендере с чашей емкостью 2л смешиваем 1л мороженого и 1л 6% молока.

Готовый коктейл разливаем по стаканчикам на 200мл. Выходит 20 порций.

Задача №1. Какую массу молока 6%-й жирности  и пломбира 50%-й жирности  необходимо взять для  приготовления 100г 28%-го новогоднего коктейля?

Решение:

	%-е содержание	Масса раствора (г)	Масса вещества (г)
Молоко Пло бир	6%=0,06 50%=0,5	х 100-х	0,06х 0,5(100-х)
Коктейль	28%=0,28	100	0,28*100

 

0,06х + 0,5(100-х) = 0,28*100

0,06х + 50 – 0,5х = 28

-0,44х = -22

х = 50

50(г) – молока

100 – 50 = 50(г) – пломбира.

                                      Ответ:50г молока,50г пломбира

Подведение итогов урока

Учитель химии.

– Посмотрите на содержание всех решенных сегодня задач. Что их объединяет?  (Задачи на растворы.)

– Действительно, во всех задачах фигурируют водные растворы; расчеты связаны с массовой долей растворенного вещества; и если вы обратили внимание, задачи касаются разных сторон нашего быта.

Учитель математики.

– Посмотрите на эти задачи с точки зрения математики. Что их объединяет?  (Задачи на проценты.)

При решении всех этих задач  мы используем правило нахождения процента от числа.

Оценки за урок.

Домашнее задание.

Решить данные задачи двумя способами и обдумать ответы на следующие вопросы:

Полезным ли для вас оказался этот интегрированный урок?

Смогли ли вы выбрать наиболее подходящий для вас способ решения?

Будете ли вы использовать эти методы в дальнейшем и при решении заданий ЕНТ?

1. Какую массу соли надо добавить к 500 грамм 10% раствора соли, чтобы раствор стал 25% ?

2. В колбе содержится 57% водный раствор соли. После выпаривания 25 грамм воды раствор стал 76 процентным. Сколько ещё надо выпарить воды, чтобы содержание воды в колбе стало равным 95%. (Ответ: 15 грамм).

3.Задача 2. Имеются два раствора кислоты разной концентрации. Объем одного раствора 4 л, другого – 6 л. Если их слить вместе, то получится 35 % раствор кислоты. Если же слить равные объемы этих растворов, то получится 36 % раствор кислоты. Сколько литров кислоты содержится в каждом из первоначальных растворов?

Рефлексия. (Синквейн)

Раствор

Разбавленный, водный

Растворять, смешивать, решать

Растворы широко встречаются в быту.

Смеси

Цель урока достигнута в случае, если знания и умения будут отвечать требованиям к уровню подготовки по данной теме.

Наш урок подошел к концу. Сейчас  каждый из вас оставит на парте тот смайлик, какое настроение вы приобрели на уроке.

Спасибо за урок!

Приложение №2

Само оценивание достижений на уроке

Лабораторная работа

Ознакомьтесь с критериями оценивания ваших навыков в ходе лабораторной работы. В нужной колонке отметьте ваш уровень достижений.

Что оцениваем	Отличный	Хороший	Средний
Ваше отношение к технике эксперимента	Вам требуется минимальная помощь при работе с лабораторным оборудованием. Практически не требуется помощи при соблюдении правил техники безопасности или вы самостоятельно следуете правилам техники безопасности. Эффективно сотрудничаете с другими.	Иногда требуется помощь и наблюдение со стороны учителя при работе с лабораторным оборудованием. Иногда нуждаетесь в помощи при соблюдении правил техники безопасности. Часто сотрудничаете с другими.	Требуется постоянная помощь и наблюдение со стороны учителя при работе с лабораторным оборудованием. Нуждаетесь в постоянном напоминании о соблюдении правил техники безопасности. Редко сотрудничаете с другими.
Проставь отметку (+)
Научное исследование Опыты на уроке	Вы самостоятельно определяете цель исследования. Пытаетесь сформулировать гипотезу. Следуете методу предложенному учителем. Пытаетесь предложить способы улучшения работы.	Вы организуете и презентуете данные, используя форму предложенную учителем. Иногда требуется помощь. Пытаетесь делать простые выводы.	Пытаетесь презентовать данные, используя форму предложенную учителем. Постоянно требуется помощь.
Проставь отметку(+)
Тестирование	Анализируете и оцениваете научную информацию. Приводите научно обоснованные суждения по поводу обоснованности и идей или качества работы.	Анализируете научную информацию, определяете составные части, взаимосвязи. Даете объяснение, демонстрируете понимание.	Упоминаете идеи и концепции для решения простых проблем.
Укажите количество правильных ответов (+)	90%	80%	70%