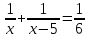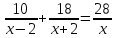Учащиеся должны уметь решать задачи с помощью квадратных уравнений.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Решение текстовых задач с помощью квадратных уравнений.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Решение текстовых задач с помощью квадратных уравнений.»
Полезное для учителя
Распродажа видеоуроков!
2100 руб.
3000 руб.
2000 руб.
2860 руб.
1760 руб.
2510 руб.
2020 руб.
2880 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
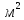 . Сколько необходимо мне закупить материала? Возможно ли, решить задачу с помощью квадратного уравнения?
. Сколько необходимо мне закупить материала? Возможно ли, решить задачу с помощью квадратного уравнения?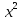 +6х=187,
+6х=187,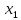 =
=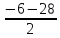 =-17,
=-17, 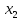 =
=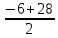 =11.
=11.