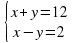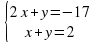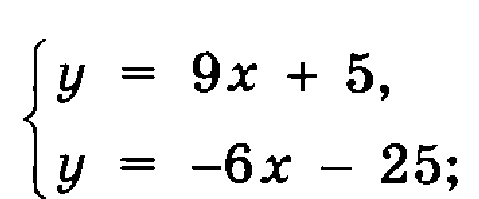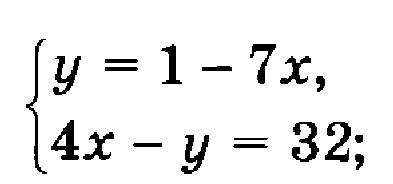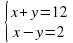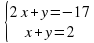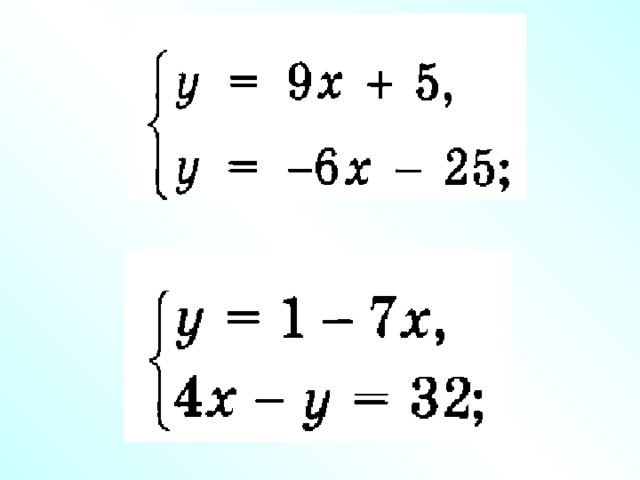Решение систем линейных уравнений. Метод подстановки.

Деятельность учителя

Деятельность учеников

Организационный момент

Учитель приветствует учащихся, проверяет их готовность к уроку;

Проводит инструктаж по работе с технологической картой: На столах у вас лежат листочки, листы самооценки. Сегодня вы будете работать на этих листах. Подпишите их. В течение урока мы с вами будем выполнять различные задания. Если задание будет выполнено верно, то вам необходимо в квадрат, находящийся справа, поставить балл за выполненное задание. Те из вас, кто решит задания быстрее класса, могут заработать дополнительную оценку, выполнив дополнительные задания

Подписывают листы самооценки.

1. Устный счет. Актуализация и фиксирование индивидуального затруднения в пробном действии. (4-5 мин)

1) Найти значение функции при заданном значении аргумента

1вариант: y=5x-4 -4; 2

2вариант: y=3x-7 1; - 2)

2) Преобразуйте линейное уравнение с двумя переменными к виду линейной функции y=kx+m

1вариант:

5x-y-8=0

6x+2y-5=0

2вариант:

9х-y-4=0

4x+2y-7=0

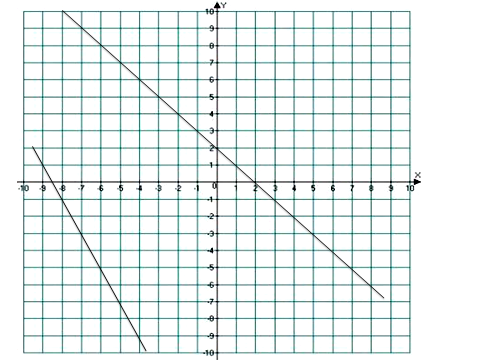
3) Не выполняя построений найдите точки пересечения прямых.

^{1вариант:}

y=-х+3 и y=2х

y=3х-8 и y=-2х+7

2вариант:

y=-5х и y=3х-16

y=-3х-5 и y=4х+9

Заполняют таблицу

Взаимопроверка с комментированием

1. Постановка учебной задачи(4-5 мин)

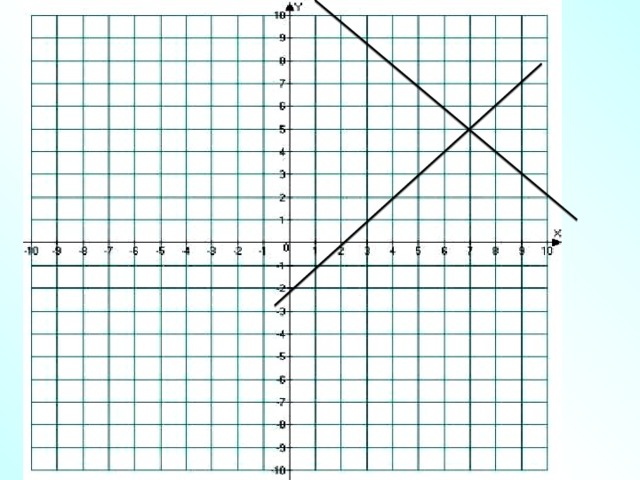
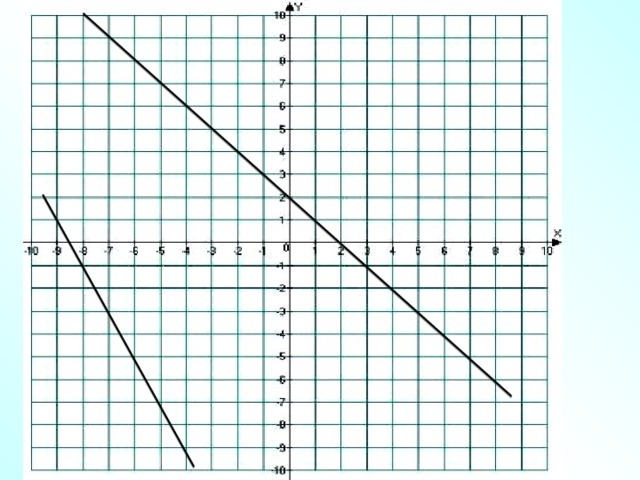
Решим системы линейных уравнений с двумя переменными. Но для этого нам необходимо вспомнить, а что мы знаем о системах?

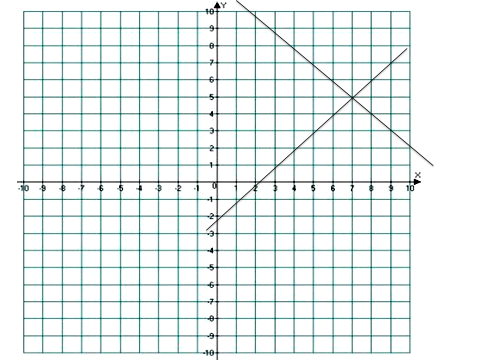
Значит решим две системы графически.

Что вы хотите узнать?

Это и будет нашими целями на урок.

Системы линейных уравнений

Решением системы двух уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство.

Решить систему уравнений – значит найти все ее решения или доказать, что решений нет.

Решением системы уравнений, будет являться точка, в которой пересекаются прямые.

Нам известен графический метод решения.

Алгоритм решения системы линейных уравнений с двумя переменными графическим способом:

1. Строим в координатной плоскости графики каждого уравнения системы, т.е. две прямые (опираясь на алгоритм построения графика линейного уравнения с 2 переменными).

2. Отыскиваем точку пересечения графиков. Записываем ее координаты.

3. Делаем вывод о числе решений системы.

4. Записываем ответ.

(7;5)

Вторую систему решить графически не получается

Хотим узнать новый метод решения систем линейных уравнений.

1. “Открытие” учащимися нового знания. (7-8 мин)

Что значит система имеет единственное решение?

Как найти, не графически, координату этой точки пересечения?

Давайте так и сделаем.

Но мы же не можем каждый раз решать «на ощупь». Значит нам необходим…

Инструктаж: возьмите конверт с разрезанным на части алгоритмом решения систем. Вам нужно:

1) собрать алгоритм на листе бумаги, пронумеровав его части.

2) воспользоваться готовым алгоритмом при решении предложенной вам системы

3) проверить правильность выполнения заданий

Значит прямые пересекаются. То есть имеют одну общую точку. Значит в этой точке принимают одинаковые (равные) значения (x;y)

Если равны левые части, можно приравнять и правые части.

(-19;21)

АЛГОРИТМ

1) Выбрать одно уравнение (лучше выбирать то, где числа меньше) и выразить из него одну переменную через другую, например, x через y. (можно и y через x).

2) Полученное выражение подставить вместо соответствующей переменной в другое уравнение. Таким образом, у нас получится линейное уравнение с одной неизвестной.

3) Решаем полученное линейное уравнение и получаем решение.

4) Подставляем полученное решение в выражение, полученное в первом пункте, получаем вторую неизвестную из решения.

5) Выполнить проверку полученного решения.

1. Первичное закрепление. (4-5 мин)

Работа в парах, решение систем уравнений используя алгоритм

Рефлексия

Что мы знали?

Что хотели узнать?

Что узнали?

Достигли ли мы цели, которую ставили на уроке?

А теперь подсчитаем количество баллов и переведем в оценку.

Домашнее задание:

п. 12, алгоритм, №12.1(в,г), 12.3(в,г), 12.4(в,г)

Знаю

Хочу узнать

Узнал

Задание

Кол-во баллов

Устный счет

1. Найти значение функции при заданном значении аргумента

2. Преобразуйте линейное уравнение с двумя переменными к виду линейной функции y=kx+m

3. Не выполняя построений найдите точки пересечения прямых.

Алгоритм

Решение систем линейных уравнений

Общее количество баллов

Оценка

«2»:менее 3 баллов

«3»: от 3 до 5 баллов

«4»: от 6 до 8 баллов

«5»: от 9 до 11 баллов

х

у

х

у

х

у

х

у