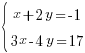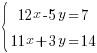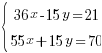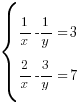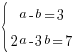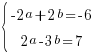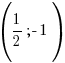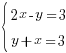Решение систем линейных уравнений

Решение систем линейных уравнений

Существует три способа решения систем линейных уравнений:

• Способ подстановки

• Способ сложения

• Графический способ.

Остановимся на каждом из них подробно.

1. Способ подстановки удобно использовать в том случае, если в одном из уравнений системы коэффициент при одном из неизвестных равен 1. Тогда это неизвестное удобно выразить через другое.

Решим систему:

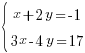
Заметим, что в первом уравнении системы коэффициент при 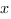 равен 1, поэтому мы легко можем выразить  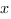через :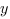

.

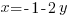Подставим это выражение для 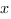 вместо переменной 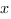во второе уравнение системы:

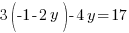
Решим это уравнение относительно :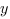

.

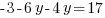
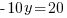
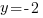Теперь вспомним, что 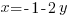. Подставим в правую часть равенства вместо переменной  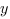ее значение и найдем значение :

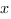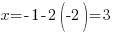
Внимание! При записи ответа на первом месте всегда указываем значение переменной 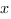, а на втором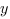 

Ответ: (3;-2)

2. Способ сложения более универсален, нежели способ подстановки.

Решим систему:

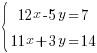
Мы имеем право умножать каждое уравнение системы на число и складывать уравнения. Воспользуемся этим правом.

Нам нужно сделать так, чтобы коэффициенты при одном из неизвестных были равны по модулю, но противоположны по знаку. Тогда при  сложении уравнений это неизвестное пропадет.

Сделаем так, чтобы, например, коэффициенты при 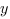были равны по модулю, но противоположны по знаку. Для этого нам нужно первое уравнение системы умножить на 3, а второе на 5. Получим систему:

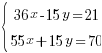
Сложим уравнения системы, получим

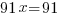, отсюда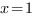 

Теперь подставим это значение 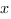, например, в первое уравнение исходной системы:

;

;

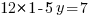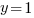
Ответ: (1;1)

А теперь решим такую систему:

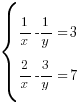
Уравнения системы не являются линейными. Но мы можем сильно упростить себе жизнь, если введем замену переменной. Поэтому прежде чем решать эту систему, введем замену 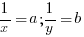. Получим систему линейных уравнений:

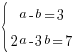
Мы можем решать эту систему как способом подстановки (коэффициент при 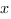 в первом уравнении равен 1, а при  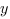-1), так и способом сложения.

Решим способом сложения. Умножим первое уравнение на -2, тогда коэффициенты при 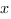 будут равны по модулю, но противоположны по знаку.

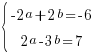
Сложим уравнения. Получим:

; 

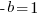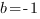
Подставим это значение 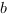 в первое уравнение исходной системы: ; 

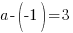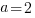
Итак,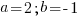 

Вернемся к исходной переменной:

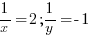
отсюда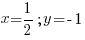 

Ответ: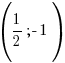 

3. Графический способ.

Чтобы решить систему линейных уравнений графическим способом, нужно

• в каждом уравнении выразить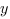 

• построить графики соответствующих функций

• найти координаты точки пересечения графиков.

Решим систему

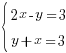
1. В каждом уравнении выразим :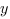

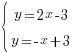
2. Построим графики этих функций:

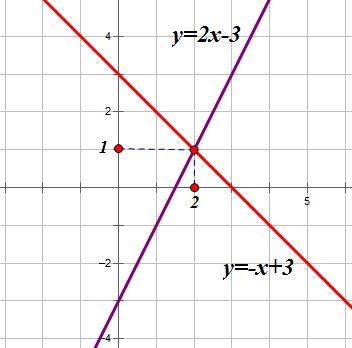
Координаты точек точки пересечения графиков (2;1)

Ответ: (2;1)

В течение всех лет обучения в школе решают различные виды уравнений и неравенств. Не сосчитать, сколько линейных, квадратичных, дробно-рациональных уравнений и неравенств решили ученики за эти годы. Однако в старших классах при решении показательных или логарифмических уравнений, когда после преобразований ученик переходит к алгебраическому уравнению, он все равно допускает ошибки. Это неудивительно: решение уравнений и неравенств – один из наиболее трудных вопросов. Действительно, чтобы правильно решить уравнение или неравенство, нужно уметь проводить тождественные преобразования входящих в него выражений, нужно уметь безошибочно вычислять, нужно знать, какие способы решения уравнений (неравенств) в каких случаях целесообразнее применить.
Очевидно, что уравнения и неравенства, изучаемые в старшей школе, осваиваются учащимися хуже, так как на их рассмотрение отводится незначительное количество часов, а при их решении ученику необходимо владеть комплексом умений, полученных в основной школе, а также новыми знаниями, связанными с каждым из новых видов уравнений. Такого объема упражнений, который обычно предлагается в учебниках по алгебре и началам анализа для 10–11-х классов, явно недостаточно для формирования умения решать показательные, логарифмические и тригонометрические уравнения (неравенства). Восполнить этот пробел поможет пособие«Учимся решать уравнения и неравенства» (авторы: Л.О. Денищева, Н.В. Карюхина, Т.Ф. Михеева).

Это учебное пособие состоит из трех глав.

В главе 1, состоящей из пяти параграфов, рассматриваются стандартные методы решения тригонометрических, показательных и логарифмических уравнений и неравенств. В начале главы (§§ 1, 2) учащимся напоминается решение простейших уравнений и неравенств. Для приведения знаний в систему и для обеспечения их лучшего запоминания этот материал сведен в таблицу и снабжен графическими иллюстрациями.

Приведем фрагмент таблицы, относящийся к решению простейших тригонометрических неравенств.

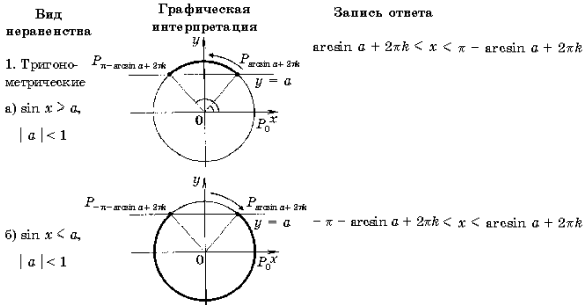
Параграфы 1, 2 снабжены большим числом тренировочных упражнений. Например, учащимся предлагается решить 25 простейших тригонометрических неравенств, в которых задействованы все табличные значения тригонометрических функций. Выполнение этих заданий не должно затруднить учащихся и занять у них много времени, так как предполагается, что при решении школьники будут активно использовать рабочую таблицу и поэтому им не нужно каждый раз чертить тригонометрический круг и делать необходимый рисунок. Для решения неравенства учащийся из таблицы выбирает нужный рисунок («а» или «б»), вычисляет необходимое значение арксинуса (или другой тригонометрической функции) и записывает ответ.

В этих же параграфах (§§ 1, 2), кроме простейших, предлагается решить уравнения и неравенства, которые за один «шаг» (с помощью элементарных алгебраических преобразований) приводятся к простейшим. Здесь строится «лесенка сложности» заданий, в ходе выполнения которых закрепляется решение простейших уравнений и неравенств.

Например, тригонометрические уравнения здесь представлены следующими задачами. (Пояснение. Нумерация дана как в учебном пособии.)

Далее (§ 3) рассматривается применение при решении тригонометрических, показательных и логарифмических уравнений (неравенств) формул тождественных преобразований выражений. В теоретической части параграфа обсуждается вопрос о возможном расширении или сужении области определения выражения в ходе его тождественного преобразования. Даются примеры преобразований, приводящих к потере корней уравнения (неравенства).

Приведем пример, где учащимся показывается, какое преобразование нужно выполнить и как записать преобразованное выражение так, чтобы в ходе решения не потерять корни уравнения.

В § 3 содержится более 100 уравнений и неравенств, легко сводящихся к простейшим в результате тождественных преобразований выражений, входящих в уравнение (неравенство). Материал этого параграфа ориентирован таким образом, чтобы обеспечить обучающую функцию. В этой связи задания разбиты по содержательно-смысловым блокам. Выделены три тематических блока: показательные уравнения (неравенства), логарифмические уравнения (неравенства) и тригонометрические уравнения (неравенства). Каждый из названных блоков имеет свою структуру. Например, в блоке, содержащем логарифмические уравнения, выделены следующие содержательно-смысловые части: применение основного логарифмического тождества, применение формул логарифма произведения или частного, применение формул логарифма степени. В соответствии с этим предлагается такая система уравнений.

Решите логарифмические уравнения

I. Примените основное логарифмическое тождество

II. Примените формулы логарифма произведения и частного

III. Примените формулу логарифма степени

В §§ 4, 5 представлены известные из основной школы методы решения уравнений: сведение исходного уравнения (с помощью замены)к квадратному и разложение на множители. В теоретической части этих параграфов приводятся возможные образцы записи решений; вводятся алгоритмические предписания, в которых реализуется данный метод решения.

Поскольку в программе по математике и в практике преподавания меньше внимания уделяется решению неравенств, то в теоретической части этих параграфов сделан больший акцент на рассмотрение различных ситуаций, возникающих при решении неравенств. Так, например, показывается, что исходное неравенство может быть равносильно не только неравенству, но и системе неравенств, или совокупности неравенств.

Например, решим неравенство

Заметим, что 150 уравнений и неравенств, представленных в этих параграфах для самостоятельного решения, предполагают прямое применение указанных методов, вырабатывая на этом этапе обучения стереотип решения.

В главе 2 рассматриваются нестандартные методы решения уравнений и неравенств, основанные на использовании свойств функций. Здесь предложены два параграфа: § 1. Ограниченность; § 2. Монотонность. Заданиям для самостоятельного решения предпослан разъяснительный текст, в котором раскрывается сущность указанного метода, показывается образец рассуждений, в которых для нахождения корней уравнения (неравенства) используется свойство функции. Приведем фрагмент объяснения из § 2.

§ 2. Монотонность

Рассмотрим задание: найти положительные корни уравнения

2^x = – x² + 3.

Как и к уравнениям из предыдущего параграфа, к этому уравнению нельзя применить стандартные приемы решения. Однако один корень этого уравнения легко угадывается (x = 1). Если посмотреть на эскиз графиков функций y = 2^x и y = – x² + 3, то можно предположить, что на промежутке [0; Ч) найденное решение единственное. Действительно, на этом промежутке «получилась» единственная точка пересечения графиков функций (см. рисунок).

Но нельзя считать задание выполненным, если не обосновать, что других положительных корней уравнение не имеет. Для доказательства заметим, что функция y = 2^x возрастает, а функция y = – x² + 3 убывает на промежутке [0; Ч), а значит каждое свое значение они принимают ровно один раз. Таким образом, «увиденный» нами корень x = 1 является единственным на заданном промежутке.

Рассмотрим неравенство

Областью определения данного неравенства является множество неотрицательных чисел. Очевидно, что на этом промежутке произведение  принимает значение, равное 1, при x = 9. Действительно,

Функции  являются монотонно возрастающими, следовательно при x  9 их значения будут больше, чем число 1, а значит и произведение также окажется большим единицы. Эти рассуждения приводят нас к заключению, что решением исходного неравенства будет промежуток [9; ).

При решении этих двух заданий нами применялось свойство монотонности.

В главе 3 приведены материалы для подготовки учащихся к экзаменам – выпускному из школы и вступительному в вуз. Здесь собраны интересные и поучительные уравнения и неравенства, предлагавшиеся ранее на выпускных экзаменах за курс общеобразовательной школы и на вступительных экзаменах в педагогические и технические вузы. Задания этой главы распределены по уровню сложности, но выбор метода решения предстоит сделать ученику на основе анализа исходного уравнения или неравенства. Чтобы показать школьникам, какие наблюдения и рассуждения помогают выбрать рациональный метод решения, в начале параграфа обсуждаются подходы к решению нескольких уравнений и неравенств. Приведем пример.

Пример 3. Решить неравенство

Решение. при всех x, кроме  так как Значит, исходное неравенство равносильно системе

Неравенству x² + 2x  0 удовлетворяют значения промежутка [– 2; 0]. Остается исключить из него число вида Таким числом является при n = – 1 число