Работая в школе, заметила, что у большинства учащихся наблюдается снижение результативности учебной деятельности, отрицательное отношение к учению – не желание учиться, слабая заинтересованность в успехах, нацеленность на отметку, не умение ставить цели, преодолевать трудности. Изучив педагогическую литературу по данной проблеме, пришла к выводу, что процесс повышения мотивации должен стать значительной частью работы учителя, поэтому на своих уроках применяю дифференцированный подход к обучению учащихся.
Дифференцированное обучение – это форма организации учебного процесса, при которой учитель работает с группой учащихся, составленной с учетом у них каких-либо значимых для учебного процесса общих качеств (гомогенная группа);
Дифференциация обучения (дифференцированный подход в обучении) - это:
создание разнообразных условий обучения для различных школ, классов, групп с целью учета особенностей их контингента;
Комплекс методических, психолого-педагогических и организационно-управленческих мероприятий, обеспечивающих обучение в гомогенных группах.
Принцип дифференциации обучения - положение, согласно которому педагогический процесс строится как дифференцированный. Одним из основных видов дифференциации (разделения) является индивидуальное обучение.
Технология дифференцированного обучения представляет собой совокупность организационных решений, средств и методов дифференцированного обучения ,охватывающих определенную часть учебного процесса.
Проблема дифференцированного подхода не является новой для сегодняшней школы. Однако выдвижение и развитие концептуальной идеи планирования обязательных результатов обучения позволило подойти к этой проблеме с новых позиций. Принципиальное отличие нового подхода состоит в том, что перед разными категориями учащихся ставятся различные цели: одни ученики должны достичь определенного объективно обусловленного уровня математической подготовки, называемого базовым, а другие, проявляющие интерес к математике и обладающие хорошими математическими способностями, должны добиться более высоких результатов.
В соответствии с этим в классе могут быть выделены две группы учащихся: группа базового уровня и группа повышенного уровня. Конечно, состав групп не должен быть застывшим. Желательно, чтобы любой ученик из группы базового уровня мог перейти в группу повышенного уровня, если он хорошо усвоит материал и будет свободно выполнять задания, соответствующие обязательным результатам обучения. С другой стороны, ученик из группы повышенного уровня может быть переведен в группу базового уровня, если он имеет пробелы в знаниях или не справляется с темпом продвижения группы.
В структуре математических способностей в педагогической литературе выделяются более десяти групп компонентов. Но мы проанализируем две основные: быстроту усвоения и активность мышления.
I группа—быстрота усвоения. Характеризуется следующими категориями:
(1) Дословное повторение текста.
(2) Частичное повторение.
(3) Воспроизведение 50 % текста.
(4) Самостоятельное воспроизведение ранее изученного текста.
(5) Воспроизведение материала с помощью учителя.
(6) Воспроизведение с ошибками, но основная нить вопроса удерживается.
(7) Замедленное, невнятное воспроизведение текста.
(8) Умственная отсталость (затухание развития).
II группа— активность мышления. Характеризуется пятью категориями:
(1) Плодотворная работа на протяжении всего урока.
(2) Работа со «вспышками».
(3) Неполная работоспособность.
(4) Быстрая утомляемость.
(5) Игнорирование заданий.
Три уровня математических способностей: уровень А - учащиеся, имеющие хорошие математические способности (I группа, категории (1) — (4); II группа, категории (1) — (2)); уровень В — учащиеся, имеющие, средние математические способности (I, (4) — (6); II, (2) - (3));
уровень С — учащиеся, имеющие низкие математические способности (I, (7) — (8); II, (4)-(5)). Период разделения класса по уровням приходится на VI класс. Два предыдущих года обучения в средней школе учащиеся подвергаются наблюдению и диагностике. Для получения большей информации о каждом ребенке учитель предлагает всем учащимся заполнить разного рода анкеты. Одна из них приводится ниже.
АНКЕТА
1. Класс...
2. Фамилия, имя...
3. Где и кем работают родители?
4. Отношение родителей к математике? (Имеют математическое образование; применяют математику в своей работе; увлечены математикой, не любят математику, совсем не интересуются ею). Подчеркнуть нужное.
5. Есть ли в домашней библиотеке математические книги, но не учебники по математике для средней школы? (Да, нет). Подчеркнуть нужное.
6. Кто больше всего помогает готовить уроки по математике?
7. Сколько времени занимает подготовка к математике?
8. Почему ты учишь математику? (Желательно ответить откровенно и полно.)
9. Хочешь ли ты знать больше, чем дают на уроке? (Да, нет.) Подчеркнуть нужное.
10. Как дается тебе математика? (Легко, много надо заучивать, трудно). Подчеркнуть нужное.
11. Твое отношение к математике? (Люблю; учу, чтобы получить хорошую оценку; чтобы не ругали дома; скучно на уроках; не хочу ее учить). Подчеркнуть нужное.
12. Какими знаниями по математике ты владел до прихода в школу? (Счет до 10 и обратно; сложение в пределах десятка; решение простых задач.) Подчеркнуть нужное.
13. Какого вида задания по математике тебе нравятся больше? (Задачи, примеры, задачи и примеры). Подчеркнуть нужное.
14. Мечтаешь ли ты связать свою жизнь с математикой? (Буду математиком; хочу поступить в вуз, где нужно будет сдавать математику; хочу знать как можно больше о разном, не только о математике.) Подчеркнуть нужное.
После того, как в одном классе сформировались три группы учащихся, по-разному относящихся к математике. О том, в какую группу попал данный ученик, обязательно сообщалось его родителям. Беседа с родителями проходит в доброжелательном тоне. И родители, и учащиеся должны будут понять, что состав группы не закреплен раз и навсегда. Впоследствии можно перейти из одной группы в другую в соответствии с результатами обучения и желанием учащегося. Период неустойчивого состояния групп продолжается в VI—IX классах.
Характеристика групп.
Учащиеся первой группы (“наименее успешные”) имеют пробелы в знаниях программного материала, искажают содержание теории в применении ее к решению задач, самостоятельно могут решить задачи в 1-2 шага, решение более сложных задач начинают со слепых проб, не умеют вести целенаправленный поиск решения, не могут найти связи между данными и искомыми величинами; часто пропускают обоснование гипотез, сформированных в ходе попыток, и не понимают необходимости их проведения, не видят существенных зависимостей и ключевых моментов в решении задач. Здесь могут быть учащиеся имеющие пробелы в знаниях и отстающих в развитии вследствие частых пропусков по болезни или в силу систематической плохой подготовки уроков. В месте с тем эту группу составляют учащиеся, относящиеся к разным уровням обучаемости. Те из них, кто имеет высокий уровень обучаемости, после ликвидации пробелов в значениях и при соответствующем обучении обычно быстро переходят на более высокие уровни развития.
Учащиеся второй группы (“успешные”) имеют достаточные знания программного материала, могут применять их при решении стандартных задач. Затрудняются при переходе к решению задач нового типа, но овладев методами их решения, справляются с решением аналогичных задач, не справляются с решением сложных (нетиповых) задач. У этих учащихся не сформированы эвристические приемы мышления, они с большим трудом могут сформировать гипотезу относительно конечной цели в поиске решения задачи.
Третью группу (“наиболее успешные”) составляют учащиеся, которые могут сводить сложные задачи к цепочке простых подзадач, выдвигать и обосновывать гипотезы в процессе поиска решения задач, переносить прежние знания в новые условия. Эти учащиеся быстро и легко обобщают методы решения классов однотипных задач, совершенно отчетливо выделяют ключевую подзадачу в решенной, могут сформулировать ее в ходе поиска решения самостоятельно или с небольшой помощью учителя, находят несколько способов решения задачи, используют эвристические приемы, но обычно неосознанно.
Выделяются два типа дифференциации обучения: дифференциация внешняя и внутренняя (внутриклассная).
Внутренняя дифференциация учитывает индивидуально-типологические особенности детей в процессе обучения их в стабильной группе (классе), созданной по случайным признакам. Разделение на группы может быть явным или неявным, состав групп меняется в зависимости от поставленной учебной задачи.
Внешняя дифференциация - это разделение учащихся по определенным признакам (способностям, интересам и т.д.) на стабильные группы, в которых и содержание образования, и методы обучения, и организационные формы различаются.
Виды дифференциации определяются, исходя из тех признаков (оснований), который лежат в основе разделения учащихся на группы. Традиционные виды дифференциации - это дифференциация по общим и специальным способностям, по интересам, проектируемой профессии.
Методику дифференцированной работы на уроке описывает В.В. Куприянович в своей статье «Изучение способностей направляет дифференциацию».(1 ) Дифференциация начинается в VI классе. Перед учителем уже не класс в общем, а три отдельные группы, объединенные, отношением к математике. Фактически это три класса в одном и три плана в одном плане урока. На первых порах трудно всем: учителю, ученикам, предметникам, работающим в этом классе.
Но впоследствии эти трудности исчезают, а умение класса организовываться для многоплановой работы на уроке окупает все издержки. Начинается поэтапное дифференцирование.
Первый этап — дифференцированная домашняя работа (особенно практическая часть). Трем группам определяются три разных задания. Группе С на дом предлагаются задания, точно соответствующие обязательным результатам обучения. Группа В выполняет такие же задания и плюс более сложные задачи и упражнения из учебника. Для группы А задания из учебника дополняются задачами из различных пособий, в особенности из пособий для поступающих в вузы.
Дифференцированная домашняя работа – такая, которая может быть рассчитана как на «сильного», так и на «слабого» ученика. Основой дифференцированного подхода на этом этапе является организация самостоятельной работы младших школьников, которая реализуется посредством следующих типичных приёмов и видов дифференцированных заданий.
Задания одинаковы для всех по содержанию, но различны по способам выполнения, например: «Вырежи из клетчатой бумаги прямоугольники одинаковой площади, равной 36 см2, но с разными сторонами». Получив такое задание, каждый ребёнок индивидуально подходит к выполнению: одни могут вырезать один прямоугольник, другие – два-три или большее число вариантов. При этом деятельность учащихся носит поисковый характер.
Задания, включающие несколько вариантов с правом самостоятельного выбора любого из них.
Одна на весь класс – самый распространённый вид домашней работы, берущий начало с дореволюционных времён и сохранившийся до наших дней. Постоянное применение таких заданий не ведёт к развитию творческих способностей учащихся, однако исключать их из арсенала педагогических средств не стоит торопиться, так как в ходе их выполнения у учащихся отрабатываются различные навыки, формируются умения.
Составление домашней работы для соседа по парте – новаторский вид домашней работы. Например: «Составь для своего соседа два задания аналогично тем, что рассматривались на уроке».
Творческую домашнюю работу необходимо задавать не на следующий день, а на несколько дней вперёд.
Если задавание уроков на дом учитель не всегда выделяет в плане отдельным пунктом, то проверка домашнего задания является по традиции частью урока.
В последние годы, подходя творчески к структуре урока, учителя используют многие разнообразные формы проверки, но преобладающей всё-таки остаётся фронтальная проверка письменных заданий. Иногда тетради с домашними заданиями собирают на проверку; в других случаях учитель просматривает тетрадь, вызывая ученика к доске. Известно, что многие учащиеся скорее находят ошибку в чужой работе, чем своей, поэтому проведение взаимопроверки, во-первых, носит воспитательный характер, а, во-вторых, повышает ответственность учеников, способствует формированию у них адекватной самооценки. О педагогическом значении проверки домашних заданий в своё время писала Н.К.Крупская: «Задавание уроков на дом тогда только целесообразно, если организован учёт выполнения заданий, качества выполнения этих заданий. Отсутствие проверки дезорганизует учащихся, понижает сознание ими ответственности. Отсутствие систематичности проверки, эпизодичность проверки также дезорганизует».
Вопрос об оценке домашних работ очень важен. Плохо, если учитель ограничивается лишь выставлением отметки. Гораздо важнее, чтобы проверка домашней работы будила мысль учеников. Многие же учителя видят в отметках единственный стимул домашней работы учащихся. Опытный учитель никогда не будет «накапливать» отметки в классном журнале путём установления очерёдности опроса по домашним заданиям, той очерёдности, которую быстро разгадывают учащиеся и поэтому не готовят уроки систематически.
А если всё-таки что-то не получилось в домашней работе? Такие случаи исключать нельзя. Опытные учителя и здесь предусмотрительны. Одни приучают школьников работать на черновике и в случае неудачи представлять черновик, которые они просматривают обычно до урока или в процессе проверки домашнего задания. Другие позволяют вместо нерешённой задачи выполнять другое задание, по выбору самого ученика, и для этого предоставляют возможность такого выбора. В любом случае они ориентируют ученика на то, чтобы он постарался объяснить, почему не получилось решение, не ограничиваясь обычным «не понял», «не сумел».
.
Второй этап — учет знаний учащихся на уроке. На этом этапе работу учителя облегчает так называемый планшет учета знаний. Он изготавливается очень просто: к куску фанеры прикрепляют «окно» из оргстекла. В «окно» вставляется список класса, а рядом с ним закрепляется начерченная на пластике таблица, в которой предусмотрены следующие графы: уровень учащегося; повторение (П); домашнее задание (Д); положительные ответы; ошибки, недочеты; общий итог, оценка. Перед уроком каждый ученик, подойдя к планшету, заполняет в строке возле своей фамилии клетки в графах «П» и «Д» (на пластике легко делаются пометки карандашом). Остальные клетки таблицы заполняет учитель во время урока; Причем он пользуется специальной символикой, чтобы учащиеся не отвлекались на занятии обсуждением оценок. Подчеркнем, что на таких уроках учитель не занимается непосредственной проверкой того, как учащиеся повторили теоретический материал или выполнили домашнее задание. Он также не привлекает консультантов-контролеров из числа учащихся. Его выводы основаны на полном доверии тому, что написано в графах «П» и «Д» в планшете учета знаний, и на том, как отвечали на вопросы во время урока. При подведении итога урока учитель выставляет оценки за работу в классе. Среди обычных оценок выделяется одна нетрадиционная. Это оценка-реабилитация, ее значение располагается между значениями оценок «2» и «3». Выставляя ее, учитель как бы говорит: «Первый раз ты действовал неудачно, но второй раз наметилось изменение к лучшему».
Третий этап — организация базового повторения. Что включается в такое повторение? Заполнение выявленных пробелов в теоретическом материале, разъяснение недочетов и ошибок в самостоятельных и контрольных работах. Материал, который учитель планирует повторить, он записывает в виде таблицы на доске или на транспаранте для кодоскопа. При разборе каждого упражнения из таблицы учитель предлагает такие, например, задания: «Выберите из Данных ответов верный», «Исправьте ошибку в данном равенстве» (для уровня С). «Назовите правило, по которому выполнялось действие», «Закончите упражнение» (для уровня В).
«Поясните причину ошибки», «Дайте определения основным понятиям, использующимся в данной задаче» (для уровня А). Учащимся уровня А можно предложить самим придумать задания и вопросы по таблице.
Четвертый этап — проверка усвоения пройденного материала. Она может проводиться в четырех режимах.
Режим «самоконтроль» предлагается учащимся из группы А;
учащиеся из групп В и С поочередно работают у доски (в кабинете оборудовано 1З рабочих мест у доски);
в течение урока к работе у доски привлекаются все учащиеся класса;
к доске никого не вызывают, но учащиеся рассаживаются По группам: первые две парты в каждом ряду —группа С, затем — В и последние — группа А; члены групп опрашивают друг друга по заранее составленным вопросам.
Пятый этап — изучение нового материала. Каждая тема требует особого подхода к ее объяснению.
Каждый урок «кварты» имеет свой девиз: «Изучаем», «Усваиваем», «Закрепляем», «Углубляем». Первый урок «кварты». («Изучаем») обращен одинаково ко всем учащимся. На следующих уроках проявляется дифференциация. Задания для группы А быстро переходят от обязательных к творческим («Думай и дерзай!»). Группа В сосредоточивается на упражнениях; которые требуют старания, хорошего понимания основных положений темы и умений сделать 1—2 логических шага в направлении развития этих положений («Старайся!»). Задания для группы С снова и снова возвращают учащихся к основным моментам объясненной темы («Повторяй и запоминай!»)
Шестой этап — самостоятельные и контрольные работы. Самостоятельные работы мы обычно разделяем на три вида: решение по образцу (для группы С); выделение нужного ответа из нескольких (для группы В); работа с дополнительным материалом (для группы А). Во время самостоятельных работ практикуется следующий прием. Учащийся, выполнивший задания уровня С, молча поднимает левую руку и продолжает работать над заданием следующего уровня. Учитель подходит к ученику, поднявшему руку, просматривает его тетрадь и отмечает на планшете, верно ли выполнено задание. Этот прием позволяет в течение урока проверить и оценить большинство работ.
Контрольные работы разделять по содержанию на базовые (когда проверяется обязательный материал) и так называемые объемные, в которые входят задания по всему материалу изученного курса. На одной и той же контрольной работе учащимся из группы А предлагаются задания, хоть и соответствующие программе, но повышенной сложности. Группа В обычно получает варианты № 5 и № 6 из «Дидактических материалов» для данного класса, а группа С — варианты № 1 и № 2 из того же источника.
В соответствии с уровнями дифференциации на своих уроках применяю следующие методы и формы обучения:
| Методы и формы обучения | Уровень дифференциации |
| Учащиеся с низкой успешностью обучения | Учащиеся со средней успешностью обучения | Учащиеся с высокой успешностью обучения |
| 1.Самостоятельные работы с дополнительным материалом | Сообщение | Реферат | Доклады |
| 2.Самостоятельные работы с учебником | Репродуктивные | Познавательно-творческие | Творческие |
| 3.Групповая работа (КСО) | Участник группы | | Руководи-тель группы |
| 4.Деловые игры | Участники игры | Исполнитель ролевой ситуации | Ведущие игры |
| 5.Внеклассные учебные занятия | Дополнительные занятия, консультации | | Факульта-тивы |
| 6.Работа временных групп во внеурочное время | Группы по ликвидации пробелов | | Группы для подготовки к олимпиадам |
| 7.Программированный контроль | Ответы типа «правильно» - «неправильно» | Из 5 ответов – один правильный | Из 10 ответов – несколько правильных |
| 8.Работа в парах (консультанты) | Консультируемый | | Консультант |
Предлагаю схему конструирования уроков при изучении условно взятой темы
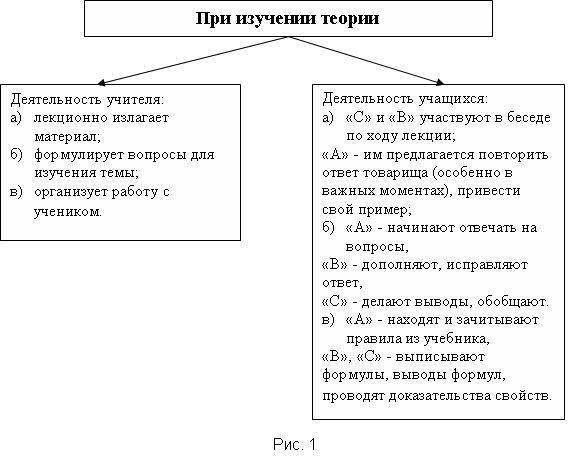
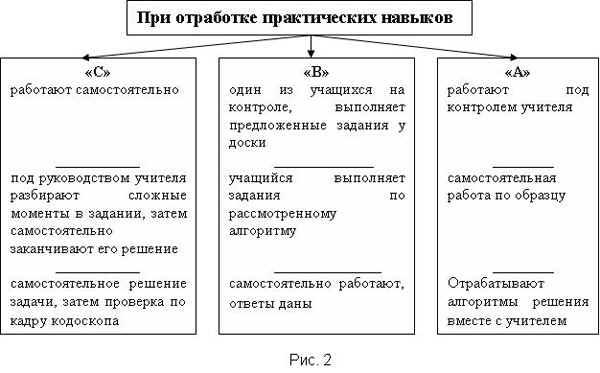
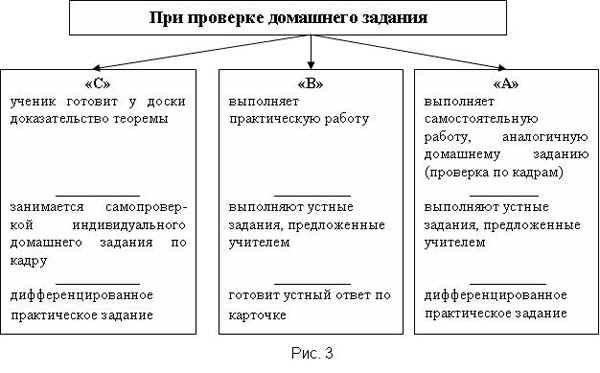
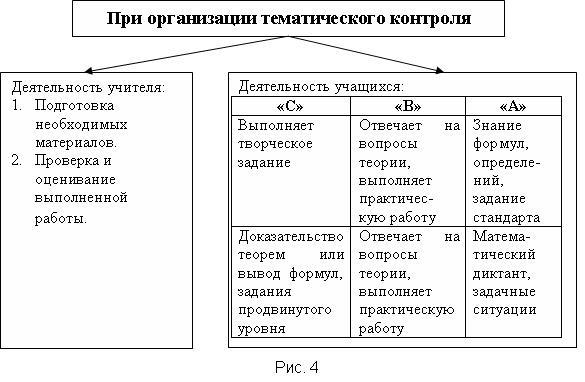
Следует отметить, что на всех этапах урока идёт одновременно работа с учениками из разных групп.
Внедряемые элементы дифференцированного подхода активизируют стремление детей к знаниям. С уроков ушло списывание и ничегонеделание. Ученики чувствуют себя ответственными за процесс обучения, приучаются к самоорганизации учебного труда.
Одним из существенных моментов в организации обучения является контроль за знаниями и умениями учащихся. От того, как он организован, на что нацелен существенно зависит содержание работы на уроке, как всего класса в целом, так и отдельных учащихся. Вся система контроля знаний и умений учащихся должна планироваться таким образом, чтобы охватывались все обязательные результаты обучения для каждого ученика. Одновременно в ходе контроля надо дать учащимся возможность проверить себя на более высоком уровне, проверить глубину усвоения материала. В ходе изучения темы учитель проверяет результаты обучения путем проведения текущих самостоятельных работ, устного опроса, контрольных работ и других форм контроля .Я использую различные способы контроля: устный контроль (индивидуальный, фронтальный, групповой, взаимный опрос и т.д.), письменный контроль ( математический диктант, самостоятельные работы, многовариантные и разноуровневые контрольные работы), тестовый контроль, игровой контроль (творческие задания, проектные работы, нетрадиционные уроки). В процессе отслеживания веду для каждого класса отдельную диагностическую карту, проанализировав которую, можно получить ответы на различные вопросы: доступно ли был дан учебный материал, интересен ли он был для учащихся. Эта диагностическая карта заполняется на протяжении работы по всей теме. Проанализировав результаты можно сделать выводы о собственных ошибках, скорректировать деятельность детей, направить её.
Контроль знаний учащихся является составной частью процесса обучения. По определению контроль это соотношение достигнутых результатов с запланированными целями обучения. Некоторые учителя традиционно подходят к организации контроля, используют его в основном ради показателей достигнутого. Проверка знаний учащихся должна давать сведения не только о правильности или неправильности конечного результата выполненной деятельности, но и о ней самой: соответствует ли форма действий данному этапу усвоения. Правильно поставленный контроль учебной деятельности учащихся позволяет учителю оценивать получаемые ими знания, умения, навыки, вовремя оказать необходимую помощь и добиваться поставленных целей обучения. Все это в совокупности создает благоприятные условия для развития познавательных способностей учащихся и активизации их самостоятельной работы на уроках математики.
Хорошо поставленный контроль позволяет учителю не только правильно оценить уровень усвоения учащимися изучаемого материала, но и увидеть свои собственные удачи и промахи.
Наша задача проверить не только знания, но и элементы практического усвоения, ощущения учащимися нового материала.
Поэтому нами введены новые элементы контроля:
1. Типы контроля (знания и умения)
2. Виды контроля (предварительный, текущий, итоговый)
3. Зачетная система контроля (работа с экспертами)
4. Новое планирование темы
Проблема контроля за учебной деятельностью учащихся не нова, и педагогический опыт накоплен в этой области богат и разносторонен.
Без хорошо налаженной проверки и своевременной оценки результатов нельзя говорить об эффективности обучения математике.
Основная цель контроля знаний и умений состоит в обнаружении достижений, успехов учащихся; в указании путей совершенствования, углубления знаний, умений, с тем, чтобы создавались условия для последующего включения школьников в активную творческую деятельность.
Эта цель в первую очередь связана с определением качества усвоения учащимися учебного материала – уровня овладения знаниями, умениями и навыками предусмотренных программой по математике. Во – вторых, конкретизация основной цели контроля связана с обучением школьников приемам взаимоконтроля и самоконтроля, формированием потребности в самоконтроле и взаимоконтроле.
Контроль должен быть целенаправленным, объективным, всесторонним регулярным и индивидуальным. . Формы контроля
В соответствии с формами обучения на практике выделяют 3 формы контроля: индивидуальная, групповая и фронтальная.[4]
1. Индивидуальный контроль.
При индивидуальном контроле каждый ученик получает свое задание, которое он должен выполнить без посторонней помощи. Такая форма контроля целесообразна в случае, если требуется выяснить индивидуальные знания, способности и возможности отдельных учащихся.
Такая форма контроля всегда планируется: учитель намечает, когда, кого, с какой целью спросить и какие для этого использовать средства.
2. Групповой контроль.
При проведении такого контроля класс временно делится на несколько групп (от 2 до 10 учащихся) и каждой группе дается проверочное задание. В зависимости от цели контроля группам предлагают одинаковые или разные задания.[23]
Групповую форму контроля применяют:
а) При повторении с целью обобщения и систематизации учебного материала.
б) При выделении приемов и методов решения задач
в) При выявлении наиболее рационального решения задач или доказательства теорем.
Иногда групповой контроль проводят в виде уплотненного опроса.
3. Фронтальный контроль.
При фронтальном контроле задания предлагаются всему классу. В процессе этого контроля изучается правильность восприятия и понимания учебного материала, вскрываются слабые стороны в знаниях учащихся, обнаруживаются недочеты, пробелы, ошибки в работах и ответах учащихся. Это позволяет учителю вовремя наметить меры по их преодолению и устранению.
п.4.2. Взаимный контроль
Роль взаимного контроля качества и эффективности учебной деятельности школьников трудно переоценить.
Он содействует выработке таких качеств личности, как честность и справедливость, коллективизм. Взаимный контроль помогает также учителю осуществлять проверку знаний учащихся. В массовой школе сравнительно часто используется взаимная проверка организационной готовности к уроку (констатирующей взаимоконтроль выполнения домашнего задания) и частичная, эпизодическая взаимопроверка знаний учащихся (рецензирование ответов на уроке, рецензирование письменных работ). Систематическая же взаимная проверка знаний, умений, навыков применяется весьма редко. Остановимся на методике проведения этой проверки.[5]
Каждый ученик получает карточку с вопросом, ответ на который он должен знать хорошо; на обороте карточки записаны фамилии нескольких учащихся и даты, когда они будут опрошены по этому вопросу. В каждый из указанных дней владелец карточки задает свой вопрос одному из учеников, в то же время он и сам должен ответить на вопрос, помещенный в карточке этого ученика. За день до проверки учащиеся предупреждают друг друга, на какие вопросы им придется отвечать. Взаимопроверка проводится обычно в последние три минуты каждого урока. За правильный ответ против фамилии (на обороте карточки) ученик ставит знак плюс, за неверный ответ или отказ отвечать – минус. Учитель периодически просматривает карточки взаимопроверки. В тех случаях, когда оказывалось много минусов, проводилась дополнительная взаимопроверка этих учеников во внеурочное время. В конце четверти проводится контрольный опрос всех учащихся, который позволяет выяснить не только общий уровень их знаний, но и насколько справедливо и строго каждый из них спрашивал своих одноклассников.
Взаимопроверка знаний значительно активизирует деятельность учащихся, повышает интерес к знаниям и даже нравится им. В ходе взаимного контроля раскрываются индивидуальные особенности детей, их взаимоотношения с товарищами.
п.4.3. Самоконтроль
На хорошем уроке всегда есть своя сверхзадача, которая сводится к формированию этих навыков и меняется в зависимости от темы урока. В одном случае она состоит в обучении приемам анализа, умению видеть закономерности, ставить вопросы, делать выводы.
В другом - в формировании критического отношения учащихся к результатам своей работы, требовательности к себе. Постоянного внимания учителя требует и проблема воспитания у учащихся веры в свои способности. Известно, что многие ученики боятся приступать к решению задач, алгоритм решения которых им неизвестен. Иногда проявляется страх перед трудностями, неумение преодолевать их самостоятельно. Выход здесь только один – прививать учащимся умения и навыки самоконтроля. Это важно с воспитательной, психолого-педагогической точки зрения. Ведь при этом ученики фактически участвуют в управлении своей собственной учебной деятельностью. Это порождает у них удовлетворенность своими занятиями, своей работой, позволяет им поверить в себя, в свои познавательные способности, открывает простор для творческой инициативы и самостоятельности. Укажем приемы формирования критического отношения учеников к результатам своей работы. Учащимся предлагается рассмотреть решения ряда примеров и оценить их. Обычно эти решения содержат типичные ошибки, которые надо обнаружить. Иногда требуется выяснить, верен ли ответ к заданию. Навыки самоконтроля можно развивать и на занимательных задачах, основанных на обычной житейской смекалке. Их полезно рассматривать как в младших, так и в старших классах. Эти задачи привлекают внимание всех учащихся, даже тех, которые не имеют особых успехов в математике.
Трудно удержать интерес учащихся к предмету, если преследуется единственная цель: научить школьников выполнять действия по данному образцу. Поэтому наряду с изучением алгоритмов возникает необходимость учить осознанному, творческому их применению. Приведем один распространенный прием такого обучения. Сразу после того, как учащиеся освоили все этапы алгоритма, им предлагается задача, которая решается по изученному алгоритму, но не самым рациональным способом. Более красивое решение получается, если не следовать алгоритму, а просто проанализировать условие задачи и сделать верные выводы.
На уроках геометрии иногда полезно “досочинить” задачу. Обычно для этого выбирают задачу из учебника на доказательство. Выписывают ее условие, а то, что надо доказать, придумывают сами.
Отметим еще несколько приемов работы учителя в формировании потребности в самоконтроле при обучении математике.
1. Давать определение иногда имеет смысл не в окончательном виде. Более
содержательные беседы с классом получаются тогда, когда ученики предлагают свой вариант определения, который затем уточняется.
2. Почти все упражнения, которые предлагаются ученикам, сформулированы
позитивно (доказать, найти). Появились также упражнения и другого типа (верно ли, проверить), но их очень мало. И совсем нет упражнений на опровержение утверждений, в то время как они чрезвычайно полезны.
Упражнения такого типа легко получить из задач позитивных, особенно на доказательство.
3. Если ученик дал письменное решение задачи (на доске или в тетради) с
ошибкой, то в иных случаях не надо торопиться с выставлением оценки. Если есть возможность дать ему время на нахождение собственной ошибки, то ее нужно использовать. Если ошибка будет найдена, то оценку снижать не стоит.
4. Класс работает самостоятельно. Выборочно просматривая некоторые
решения, учитель видит разнообразные ошибки, наиболее поучительные из них стоит показать всем учащимся класса.
5. На уроке предложена задача и сразу ответ к ней. У кого-то получился
другой ответ. Не стоит спешить с помощью – окажем ее только тогда, когда самостоятельные попытки найти ошибку ни к чему не привели.
6. Весьма рискованный, но заслуживающий внимания прием.
Учитель берется с ходу решать достаточно сложную задачу, причем на доске. Если ее и удается решить, то вряд ли наилучшим способом. Ученики еще раз убеждаются, что первый вариант решения не всегда является наилучшим.
В результате проведения описанной работы у учащихся начинает формироваться потребность в самоконтроле.
Обычным способом организации самоконтроля в процессе обучения математике является указание ответа (известного заранее или сообщаемого учениками друг другу). Некоторым учащимся в случае трудоемких заданий вполне достаточно свериться с окончательным результатом. Другим требуется дать промежуточные ответы. Это помогает им самостоятельно выполнять учебные задания даже в тот момент, когда у них еще не выработаны прочные навыки.
Среди учебных заданий, стимулирующих самоконтроль в работе учащихся, определенное место занимают задания с программированным контролем. Такие задания позволяют увеличить интенсивность самостоятельной учебной работы учащихся, удобны для организации фронтальной работы и коллективного обсуждения полученных индивидуальных результатов.
Последовательно работая над привитием умений, связанных с контролем и самоконтролем в математической деятельности учащихся, можно добиться заметных результатов. При этом растет общая математическая культура школьников, их работы и ответы становятся более грамотными.
§5. Методы контроля.
Среди методов контроля выделяют: устную проверку, проверку письменно-графических работ и проверку практических работ.
п.5.1. Устная проверка
Устная проверка организуется по-разному, в зависимости от ее цели и от содержания проверяемого материала. Среди целевых установок проверки можно выделить следующие: проверить выполнение домашнего задания, выявить подготовленность учащихся к изучению нового материала, проверить степень понимания и усвоения новых знаний. В зависимости от содержания она проводится по материалу предшествующего урока или по отдельным разделам и темам курса.
Методика устной проверки включает в себя две основные части:
а) составление проверочных вопросов и их задавание
б) ответ учащихся на поставленные вопросы
Составление проверочных вопросов и заданий - важный элемент устной проверки. Качество вопросов определяется их содержанием, характером выполняемых учащимися при ответе на вопросы умственных действий, а также словесной формулировкой.
При составлении вопросов всегда исходят из того, что проверять следует те знания, которые являются основными в данном курсе или относительно трудно усваиваются учащимися или которые необходимы для успешного усвоения дальнейших разделов и тем курса. На подбор вопросов оказывает влияние вид проверки: для уточнения содержания вопросов для текущей проверки необходим анализ связей изучаемого материала с ранее пройденным, а для тематической и итоговой проверки - выделение ведущих знаний и способов оперирования ими. Причем устную проверку считают эффективной, если она направлена на выявление осмысленности восприятия знаний и осознанности их использования, если она стимулирует самостоятельность и творческую активность учащихся.
Качество вопросов определяется характером умственных действий, которые выполняют учащиеся при ответе на вопрос. Поэтому среди проверочных заданий выделяют вопросы, активизирующие память (на воспроизведение изученного), мышление (на сравнение, доказательство, обобщение), речь. Большое значение имеют проблемные вопросы, которые заставляют применять полученные знания в практической деятельности.
Качество устной проверки зависит от подбора, последовательности и постановки вопросов, которые предлагаются, во первых каждый вопрос должен быть целенаправленным и логически завершенным, а во вторых должен быть предельно сжатым, лаконичным и точным.
Второй составной частью устной проверки является ответ учащегося на вопросы. В дидактической литературе выделяются два условия качественного выявления знаний ученика:
1) Ученику никто не мешает (учитель и класс комментируют ответ потом).
2) Создается обстановка, которая обеспечивает наилучшую работу его
интеллектуальных сил.
Прерывать ученика можно только в том случае, если он не отвечает на вопрос, а уклоняется в сторону. При оценке ответа ученика обращают внимание на правильность и полноту ответа, последовательность изложения, качество речи.
Приемы устной проверки используются на различных этапах урока. Выбор тех или иных приемов во многом предопределяется целью и логикой урока.
п.5.2. Проверка письменно – графических работ
Вторым широко применяемым методом контроля в обучении математике является проверка письменно-графических работ. Этот метод имеет свои качественные особенности: большая объективность по сравнению с устной проверкой, охват нужного числа проверяемых, экономия времени. Применение письменных работ используется для:
1) Проверки знания теоретического материала
2) Умения применять его к решению задач
3) Контроля сформированных навыков
В методике письменно – графических работ выделяют четыре основных этапа, которым надо уделять внимание, это подготовка, организация, проведение, анализ результатов.
При подготовке нужно: вычленить цель проверки, отобрать содержание объектов проверки, составить проверочные задания. Большую помощь при этом оказывают учебно – методические пособия “Книга для учителя”, “Дидактические материалы”, образцы проверочных работ в журнале “Математика в школе”.
При организации проверочной работы учащимся сообщается – в каких тетрадях ее выполнять, какие задания им предназначены, как озаглавить работу, как оформить решение, время выполнения работы. При этом следить за самостоятельностью выполнения работы каждым учеником.
Анализирование ответов учащихся эффективно тогда, когда оно проводится по определенным схемам (схемам поэлементного анализа). Тщательно проведенный анализ позволяет глубоко изучить пробелы и достижения отдельных учеников, выделить типичные ошибки и основные затруднения учащихся, изучить причины их появления и наметить пути их устранения.
п.5.3. Проверка практических работ
С помощью этого метода получают данные об умении учащихся применять полученные знания при решении практических задач, пользоваться различными таблицами, формулами, чертежными и измерительными инструментами, приборами.
Учитель получает отчет ученика, в котором приводится только результат или схематически описаны план практической работы и ее результаты. Это несколько затрудняет проверку и оценку каждого действия ученика. Поэтому на практике в проверочном задании приводиться алгоритм его выполнения, что позволяет осуществить такую проверку правильности действий ученика. Все работы проверяются, но оцениваются по-разному, по результатам обзорных работ оценки выставляются в журнал, по результатам тренировочных работ можно выставить лишь положительные оценки.
§6. Средства осуществления контроля.
В настоящее время создаются и распространяются такие средства, которые не требуют больших затрат времени на подготовку, проведение и обработку результатов. Среди них выделяют машинные и безмашинные средства проверки.
п.6.1. Безмашинные средства проверки
Среди безмашинных средств проверки наиболее распространены в практике работы школы устный опрос учащихся у доски, проверка учителем тетрадей с домашним заданием, математический диктант, самостоятельная и контрольная работы.
п.6.1.1. Проверка домашнего задания
Роль домашних заданий практически обесценивается, если не налажена их проверка. Учителя практикуют разные формы учета. Это и устный опрос у доски или с места по домашнему заданию, и короткая письменная работа, но, прежде всего это непосредственная проверка задания в тетрадях – фронтальная при обходе класса в начале урока и более основательная, выборочная во внеурочное время.
Проверку домашнего задания можно осуществлять в различных формах. Рассмотрим наиболее распространенные приемы проверки домашнего задания.
I прием.
У доски готовится один учащийся, класс в это время занят другой работой. Затем ученик отвечает, а остальные слушают и задают вопросы.
II прием.
Отличается от первого тем, что к доске вызывается не один, а все учащиеся. Этот прием позволяет экономить время урока. Этот широко распространенный в школе прием называют уплотненным опросом.
Необходимо отметить недостатки этих приемов:
1) Вызванным учащимся выделяется время на подготовку к ответу.
Остальным не дается время, чтобы продумать ответы на поставленные вопросы.
2) Если вызванные учащиеся отвечают плохо, то уплотненный опрос
затягивается на 15-20 минут, а других учащихся учитель вызвать не может, так как они не готовились к ответу.
Кроме таких форм контроля выполнения домашнего задания существуют и другие.
Самопроверка по образцу применяется на первом уроке после объяснения нового материала. Образец решения домашней работы записан на доске заранее. Учащиеся рассматривают решение образец и устно комментируют его, тетради у всех закрыты. Затем ребята открывают тетради и проверяют свои работы по образцу, подчеркивая ошибки. Этот способ развивает внимание и выявляет ошибки с помощью образца.
Взаимопроверка с помощью образца используется на следующем уроке. В этом случае учащиеся проверяют домашнюю работу своего соседа тоже по образцу. Как и в первом случае, окончательно тетради проверяет учитель.
п.6.1.2. Математический диктант
Математический диктант может заменить опрос по теме, заданной для повторения. Его продолжительность обычно 10-20 минут. Он представляет собой систему вопросов, связанных между собой.
Текст диктанта может быть:
1. Написан на плакате
2. Спроецирован на доску с помощью кадоскопа
3. Зачитан учителем
Существует еще такая разновидность диктанта, как математический диктант с графической записью ответа.
Приведем методику проведения диктанта.
1. Учитель полностью зачитывает текст, а учащиеся слушают, не делая
записей.
2. Учитель читает текст по фразам, делая паузы от одной до четырех минут,
чтобы дать учащимся возможность выполнить задание.
3. Когда все задания выполнены, учитель снова читает весь текст с
небольшими остановками (это дает учащимся возможность что – то исправить и сделать дополнения)
Правильные ответы записываются на доске. Ученики могут проверить диктант самостоятельно у соседа по парте.
В 5-7 классах все работы проверяются учителем. Этот метод проверки реже используется в старших классах.
С помощью математического диктанта можно проверить знание учащимися формулировок, определений, свойств, теорем, формул, умения и навыки в их использовании.
п.6.1.3. Организация самостоятельных работ
При изучении математики важно, чтобы учащиеся не только знали теоретический материал, но и умели применять его к решению задач и упражнений, обладали бы рядом навыков (вычислительными навыками, умениями преобразовывать выражения и т.д.). Эти умения и навыки могут быть по настоящему проверены только в письменной работе. Обычно самостоятельные работы проводятся после коллективного решения задач новой темы и предшествуют контрольной работе по этой теме.
При проведении самостоятельной работы учитель сталкивается со следующими затруднениями:
1. Дети заканчивают работу не одновременно, поэтому целесообразно
включать в работу дополнительные задания для тех, кто работает быстрее.
2. Трудно подобрать задания одинаково посильные всем учащимся.
3. Трудно организовать проверку самостоятельных работ.
п.6.1.4. Организация контрольных работ
Контрольная работа может быть кратковременной и долговременной.
1. Перед проведением контрольной работы необходимо определить объект
контроля, цель предстоящей работы и средства контроля.
Они должны быть сообщены учащимся.
2. В зависимости от вида заданий нужно продумать, каким образом ученик
должен их оформить.
3. Учитель должен продумать что он отнесет к недочетам, а что к ошибкам.
Из этого будет складываться оценка. Критерии оценки хотя бы в общих чертах должны быть известны учащимся.
4. Контрольная работа должна быть посильной для всех учащихся без
исключения. Сильным ученикам нужно дать задания труднее.
5. Каждой контрольной работе должна предшествовать самостоятельная
работа с аналогичными упражнениями.
6. Анализ контрольной работы необходимо проводить сразу, для этого
необходимо завершать работу за несколько минут до звонка. Желательно фрагменты решения разобрать сразу после написания работы, потому что на следующий день или позже учащиеся уже теряют интерес к содержанию работы и многие интересуются только оценкой.
7. Обязательно нужно проводить количественный и качественный анализ
контрольной работы.
Данные количественного анализа удобно представлять в виде таблицы
Но данные количественного анализа не позволяют установить уровень владения материалом конкретного ученика.
Такую возможность представляет качественный анализ. Информация, которая подвергается качественному анализу, должна включать данные о выполнении каждого задания предложенной контрольной работы каждым учеником класса.
Такие данные можно фиксировать в таблице.
Содержание основной части таблицы свидетельствует об основных ошибках учащихся, допущенных при выполнении отдельных заданий.
Анализ результатов контрольной работы может способствовать получению выводов об особенностях своей деятельности по организации усвоения школьниками учебного материала.
п.6.2. Машинные средства проверки
Для контроля знаний учащихся используют персональный компьютер. Для контроля знаний учащихся удобно применять типовые расчеты, которые включают наиболее характерные задания базового курса математики.
Перечислим некоторые преимущества использования компьютера для создания типовых расчетов:
1.Однотипные задания печатаются в любом количестве неповторяющихся вариантов;
2.Варианты, созданные с помощью компьютерных программ, проверяются значительно быстрее, так как компьютер может предоставить ответы к каждому заданию;
3.Компьютерные типовые задания удобны для отработки необходимых навыков с отстающими учащимися (учитель не тратит время на подбор однотипных заданий для отработки определенных навыков);
4.Учащиеся с огромным интересом работают с такими заданиями, особенно, если карточка с заданием индивидуальна и ученик может работать в ней.
«Если учитель будет систематически, всесторонне использовать различные формы контроля знаний и умений, то будет повышаться заинтересованность учащихся в изучении предмета, а следовательно будет повышаться и качество обучения»
Заключение.
Применение уровневой дифференциации при обучении математике, как одного из путей учета индивидуальных особенностей учащихся, необходимо и возможно. Возможность применения уровневой дифференциации а также ее эффективность подтверждается опытом многих учителей: публикациями в журнале “Математика в школе”, “Директор школы”, “Педагогика” и т.п.
Уровневая дифференциация способствует более прочному и глубокому усвоению знаний, развитию индивидуальных способностей, развитию самостоятельного творческого мышления
Описанная система дифференцированных заданий применяется мною уже в течении нескольких лет. Отмечаю, что разноуровневые задания облегчают организацию занятия в классе, создают условия для продвижения школьников в учебе в соответствии с их возможностями.
Слабые учащиеся охотно выполняют задания, содержащие инструктивный материал, особенно те упражнения, в которых приведены данные для самоконтроля. Это позволило сделать вывод, что таким школьникам недостаточно только показать ответ (как это делается в учебнике). Выяснив, что получен неверный ответ к заданию, ученик не в состоянии проследить всю цепочку и найти ошибку.
Предлагая задания творческого характера, я не рассчитывала на то, что учащиеся, тем более слабые, смогут самостоятельно их выполнить. Однако результаты показывают, что творческие задания стимулируют познавательную активность слабых школьников. Ребята, потратившие определенные усилия на творческие задания, охотно принимают участие в обсуждении этих заданий, с интересом выслушивают объяснения приемов их решения даже в тех случаях, когда они этих приемов сами найти не смогли.
Разноуровневые задания, составленные с учетом возможностей учащихся, создают в классе благоприятный психологический климат. У ребят возникает чувство удовлетворения после каждого верно решенного задания. Успех, испытанный в результате преодоления трудностей, даёт мощный импульс повышению познавательной активности. У учащихся, в том числе и у слабых, появлялась уверенность в своих силах, они уже не чувствуют страха перед новыми задачами, рисковать пробовать свои силы в незнакомой ситуации, берутся за решение задач более высокого уровня. Все это способствует активизации мыслительной
деятельности учащихся, созданию положительной мотивации.
МОУ Рассыпнянская средняя общеобразовательная школа
Доклад: « Новые формы дифференцированного
контроля знаний учащихся и методика
их проведения».
Подготовила: Горшкова Ольга
Ивановна.
2010г.

 6
6



















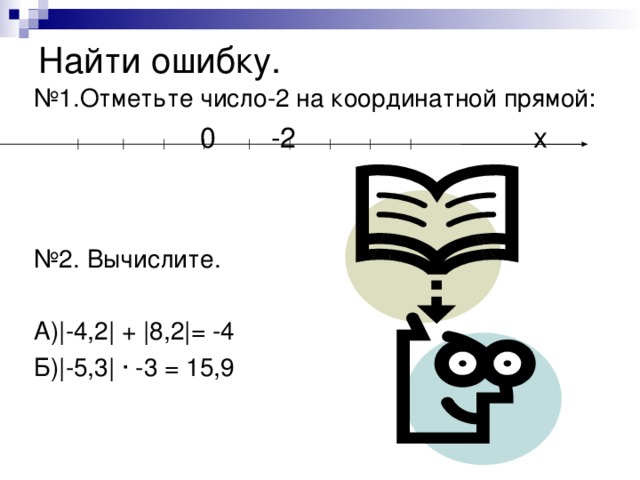
 -1,17 Б) 5 № 4. Найдите значение выражения: А) ( -3) · (-5) = 15 Б) 36 – (-8) = 28 В) -3,2 : 0,4 = -0,8 Г) 5 - 13 = 18" width="640"
-1,17 Б) 5 № 4. Найдите значение выражения: А) ( -3) · (-5) = 15 Б) 36 – (-8) = 28 В) -3,2 : 0,4 = -0,8 Г) 5 - 13 = 18" width="640"





















