Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства. В ходе урока учащиеся систематизируют, повторяют знания о свойствах планиметрических фигур, формулах; приемах и методах решения нестандартных задач практической направленности. Приобретают умения работать в группе и творчески подходить к решению учебно-исследовательской проблемы. Форма урока содействует становлению умений и опыта дискутировать, отстаивать свою позицию, доказывать, находить план решения, овладевать математическим языком, презентовать свои решения, раскрывать личностные качества.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
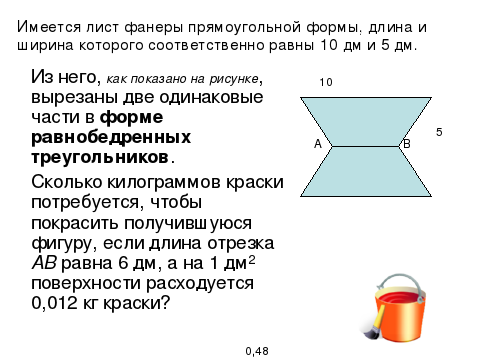
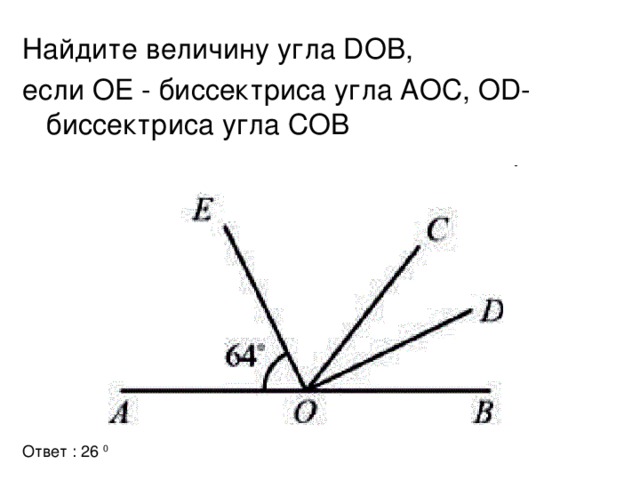
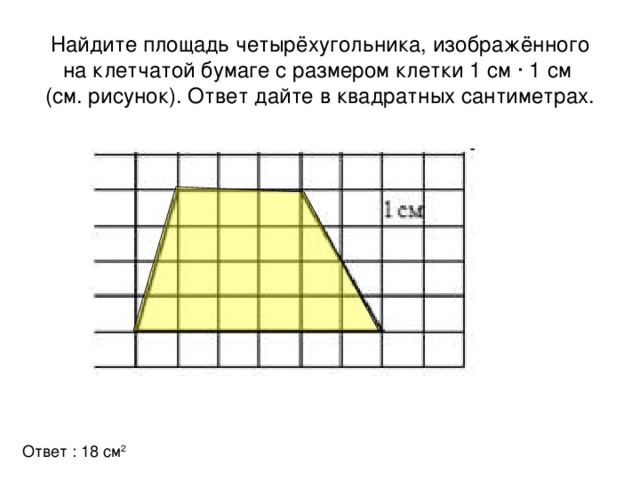
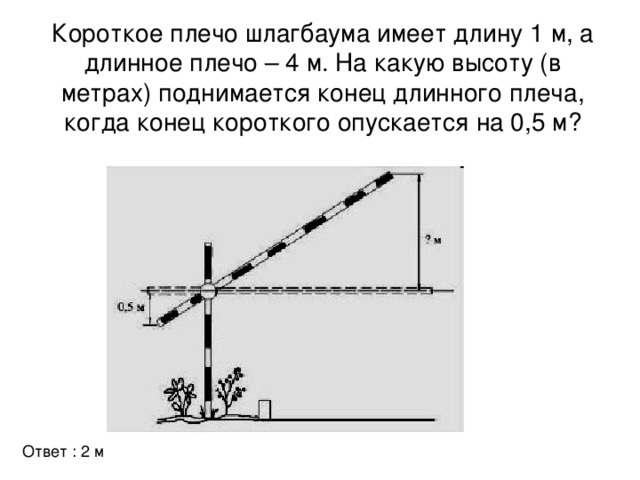
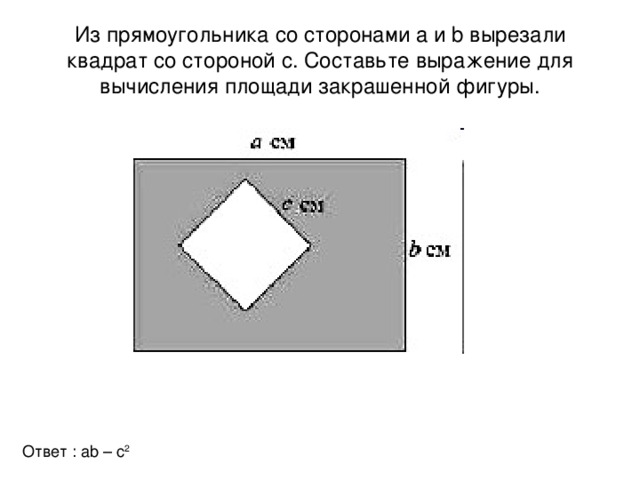
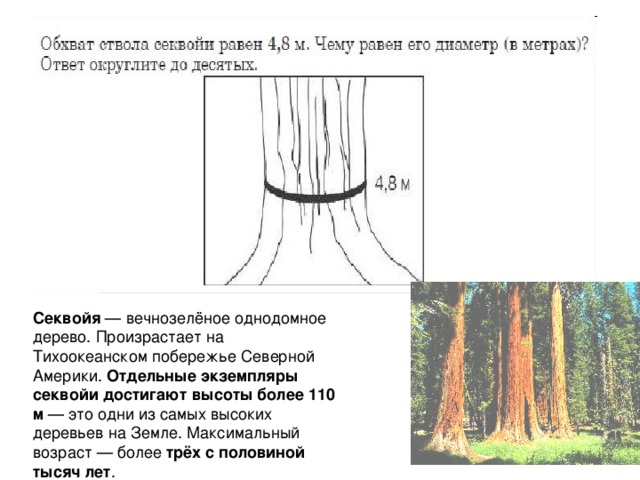
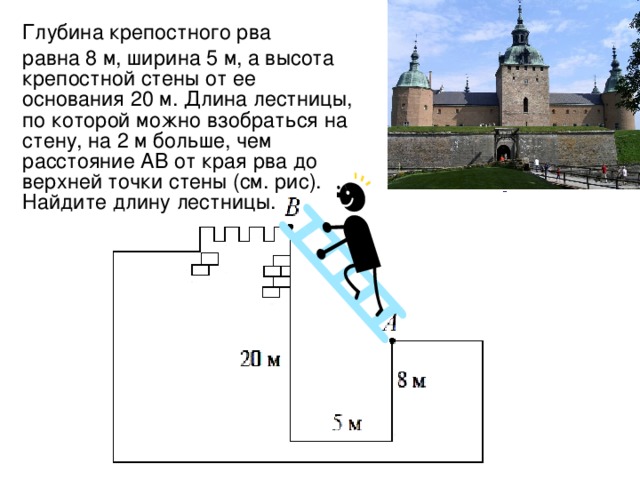
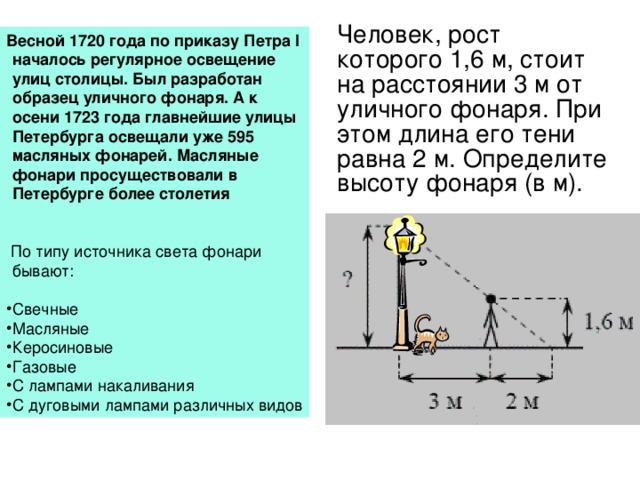
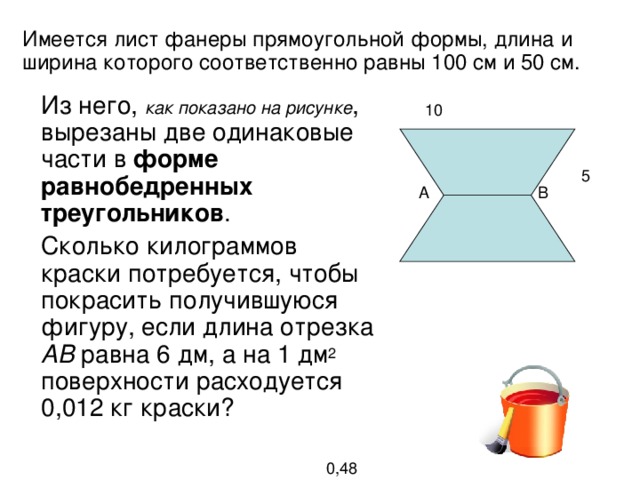
Решение геометрических задач
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«решение геом задач»
Просмотр содержимого презентации
«решение геом задач»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2220 руб.
3170 руб.
1670 руб.
2380 руб.
2020 руб.
2880 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
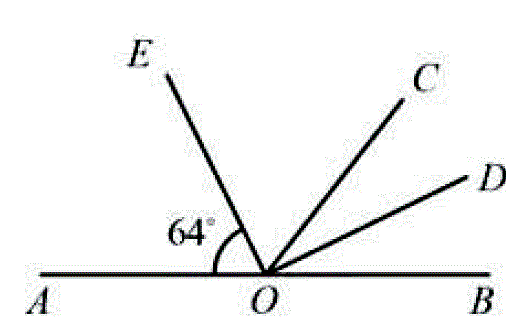 Ответ : ___________
Ответ : ___________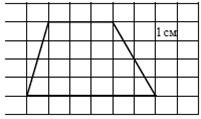 Ответ : ___________
Ответ : ___________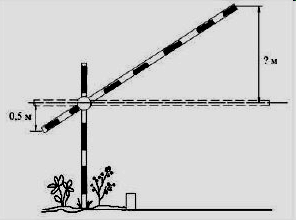 Ответ : ___________
Ответ : ___________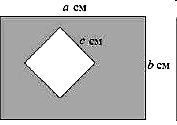 Ответ : ___________
Ответ : ___________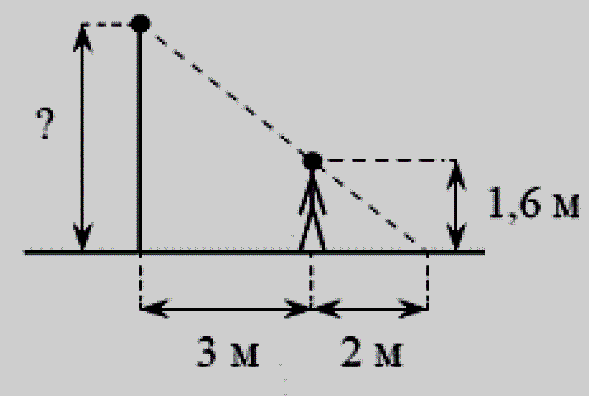 Ответ : ___________
Ответ : ___________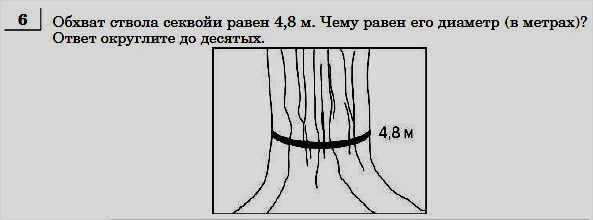 Ответ : _________
Ответ : _________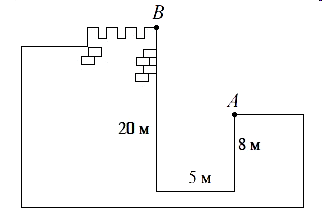 Ответ : ___________
Ответ : ___________