Мы остановимся на особенностях решения геометрических задач векторным и координатным методами. Сущность векторного и координатного методов решения геометрических задач практически одна: геометрическая задача полностью переводится на язык алгебры и дальнейшее ее решения сводится к решению уравнений, неравенств или их систем.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Методические рекомендации по теме «Особенности решения геометрических задач векторным и координатным методами».
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Методические рекомендации по теме «Особенности решения геометрических задач векторным и координатным методами».»
Полезное для учителя
Распродажа видеоуроков!
1900 руб.
2710 руб.
2000 руб.
2860 руб.
1970 руб.
2820 руб.
2020 руб.
2880 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
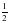 ОD. Доказать, что точка пересечения прямых СК и АМ расположена на данной окружности.
ОD. Доказать, что точка пересечения прямых СК и АМ расположена на данной окружности.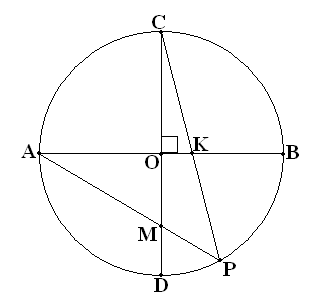
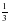 ;0); М(0;-
;0); М(0;-
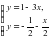

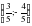
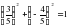 , найденная точка лежит на окружности.
, найденная точка лежит на окружности.
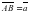 ;
;  (для краткости)
(для краткости)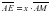 ;
; 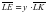

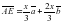 , а с другой стороны,
, а с другой стороны,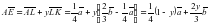
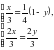 х =
х = 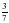 , значит АЕ:ЕМ = 3:7
, значит АЕ:ЕМ = 3:7 . Определите вид треугольника АВС.
. Определите вид треугольника АВС.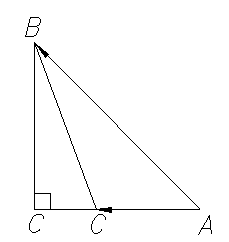
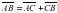 , получим:
, получим: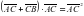 ,
,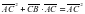 ,
, , следовательно
, следовательно 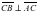
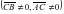 , т.е.
, т.е.  , или
, или 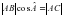 (1)
(1) (2)
(2) , т.е ÐС=ÐС1= 90, следовательно, ∆АВС – прямоугольный
, т.е ÐС=ÐС1= 90, следовательно, ∆АВС – прямоугольный















