Решение логических задач по математике

Этапы занятия. Формируемые УУД.

Деятельность педагога

Деятельность воспитанников

Организационный момент.

Личностные УУД.

Разделить учеников на три команды.

- Встало солнышко давно,

Заглянуло к нам в окно.

Торопись скорее в класс,

Интересно здесь у нас!

СЛАЙД (солнышко)

- Улыбнулись друг другу, подарите и мне свои улыбки. Спасибо! Улыбка располагает к приятному общению. Такой улыбкой можно творить чудеса.

- А теперь проверь дружок

Готов ли ты начать урок

Все на месте?

Все в порядке?

Ручка, карандаши, тетрадка?

Слушают стихотворение и настраиваются на учебную деятельность.

Улыбаются друг другу, проверяют.

Погружение воспитанников в тему внеурочного занятия.

Познавательны, коммуникативные УУД.

- Если все на месте, то начинаем наше занятие с разминки. Помните ваша задача как можно быстрее дать правильные ответы на вопросы. Имейте в виду, что есть вопросы с хитринкой. За каждый правильный вопрос вы будете получать смайлики. Вопросы задаю всем, поднимаем руки, но не выкрикиваем.

1. Как называется третий осенний месяц? (ноябрь)

2. На какой сигнал светофора надо переходить улицу? (зеленый)

3. Все пробует на зуб: и сосну, и ель, и дуб. Что это? (пила)

4. У кого рога длиннее хвоста? (лось) .

5. Каких камней на дне моря не найдешь? (сухих)

6. На каких полях трава не растет? (на шахматных)

7. Какую чашку нельзя наполнить? (перевернутую)

8. Как называется летательный аппарат Бабы – Яги? (метла)

- Веками люди мечтали подняться в космос и полетать над землей. Их фантазия создала Бабу – Ягу с ее ступой, ковер- самолет. Со временем эта мечта осуществилась. Люди придумали самолет. На  самолете можно без посадок и дозаправки топливом в полете, облететь весь земной шар.

- Ребята, а кто управляет самолетом?

- А кто из вас хотел бы побывать в кабине пилота?

- А как вы представляете себе  человека этой профессии?  Какой он? (смелый, сильный, очень умный, внимательный, наблюдательный, у него быстрая реакция, хорошая память, сильные руки…)

- А вы хотели бы обладать всеми этими качествам?

- Как вы думаете, чем мы будем заниматься на сегодняшнем нашем занятии? (мы будем развивать память, мышление, воображение…)

- Да, ребята, сегодня мы будем развивать память, мышление, воображение.

Слушают внимательно задание, настраиваются на работу.

Отвечают на вопросы, сравнивают ответы со слайдом, анализируют каждый вопрос.

Слушают учителя, рассматривают слайды, представляют.

Рассуждают, вспоминают, предполагают.

Поднимают руки.

Рассуждают, рассказывают о человеке этой профессии, анализируют, сравнивают ответы.

Предполагают, рассуждают.

Слушают учителя, анализируют, сравнивают свои размышления с выводом учителя.

Раскрытие основного содержания внеурочного занятия.

Познавательные, коммуникативные, регулятивные УУД.

- А сейчас, ребята, будем решать задачи. Посмотрите на слайд и внимательно послушайте задачу.

• 1) Поезд состоит из 12 вагонов. Марат сел в 6 по счёту вагон с головы поезда, а Андрей сел в 6 вагон по счёту с хвоста поезда. В одном ли вагоне ехали Марат и Андрей?

- О чем эта задача? Что спрашивается в задаче? Что известно в задаче?

Решают задачу вместе, записывают в тетрадях, решает у доски ученик, который поднял руку первым.

Проверка по слайду.

Те кто первый отвечает и правильно получают смайлик.

2) Колю угостили конфетами. Половину конфет он съел, а оставшиеся 5 конфет отнёс брату. Сколько конфет дали Коле?

- О чем эта задача? Что требуется найти в задаче? Что известно в задаче? Что обозначает слово «половину конфет»?

Решают задачу вместе, записывают в тетрадях, один ученик комментирует у доски.

Проверка по слайду.

Оценка смайликом.

3) Если три десятка умножить на четыре десятка, то сколько получится?

Ответ 

Получится не 12 десятков, а 120 десятков. То есть : 30 * 40 = 1200. 

4)
Можете ли вы обосновать, почему почти во всех странах мира канализационные крышки у люков имеют только круглую форму? (Квадратные крышки люков бывают лишь тогда, когда они дополнительно крепятся шарнирами).

Ответ 

Если крышки люков будут квадратными, то они могут легко провалиться в люк, т.к. диагональ квадрата больше стороны квадрата. Поэтому их если и делают, то только прикрепив к люку шарнирами. У круглых крышек люков нет диагонали и стороны, а только диаметр, который у крышки всегда больше отверстия люка. 

5)
Как вы думаете, какой знак следует поставить между 0 и 1, чтобы было получено число больше 0, но меньше 1?

Ответ 

Этот знак является запятой. То есть 0,1. Это число больше 0, но меньше 1. 

6)
Как вы думаете, сколько граней имеет шестигранный карандаш, который ни разу не затачивали?

Ответ 

Шестигранный карандаш, если не подвергался заточке будет иметь 8 граней. 6 большие грани и 2 торцевые.

- Хорошо, ребята, а теперь немножко отдохнем.

ФИЗМИНУТКА

РАБОТА В ГРУППАХ

1. Трехлитровый сосуд полностью заполнен тремя литрами воды. Вам необходимо за 2 переливания заполнить два пустых сосуда на 1 и 2 литра, чтобы в каждом из них было по 1 литру воды. При этом больше нельзя пользоваться ни чем, кроме этих трех сосудов.

Ответ 

Из полного сосуда наливаем в двухлитровый пустой ровно два литра, т.е. до краев. Далее из этого сосуда выливаем в однолитровый ровно литр воды (т.е. до краев). 
2)

 За 5 рублей куплено 100 штук разных фруктов.
     Цены на фрукты следующие: арбузы – 50 копеек за штуку, яблоки – 10 копеек за штуку, сливы – 10 копеек за десяток. 
     Сколько фруктов каждого рода было куплено?

           Ответ:      1 арбуз (50 копеек), 39 яблок (3 рубля 90 копеек), 60 слив (60 копеек).

3) Товар на 10% подорожал, потом на 10% подешевел. Когда цена его была ниже: до подорожания или после подешевления?

           Ответ:      После подешевления товар стал на 1% дешевле, чем до подорожания.

4) В магазин доставили 6 бочонков с квасом, в них было 15, 16, 18, 19, 20 и 31 литр.
В первый же день нашлось два покупателя: один купил два бочонка, другой – три, причем первый купил вдвое меньше кваса, чем второй.
Не пришлось даже раскупоривать бочонки. Из шести бочонков на складе остался всего лишь один. Какой?

           Ответ:      Первый покупатель купил 15-литровый и 18-литровый бочонки. Второй – 16-литровый, 19-литровый и 31-литровый. Остался непроданным 20-литровый бочонок.

5) Изделие весит 89,4 грамма. Сообразите в уме, сколько тонн весит миллион таких изделий.

           Ответ:      Миллион изделий весит 89,4 тонны.

6) Банка с медом весит 500 граммов. Та же банка с керосином весит 350 граммов. Керосин легче меда в 2 раза. Сколько весит пустая банка?

           Ответ:      Пустая банка весит 200 граммов.

7) Круглое бревно весит 30 килограммов. Сколько бы оно весило, если бы било вдвое толще, но вдвое короче?

           Ответ:      Бревно весило бы 60 килограммов.

8) Чтобы сжить с белого света Змея Горыныча, которому исполнилось 40 лет, Кощей Бессмертный придумал приучить его к курению.
Кощей Бессмертный подсчитал, что если Змей Горыныч каждый день в течение года будет выкуривать по 17 сигарет,
то он умрет через 5 лет, если же он будет выкуривать по 16 сигарет, то умрет через 10 лет.
До скольких лет доживет Змей Горыныч, если он не будет курить?

           Ответ:      Некурящий Змей Горыныч проживет до 130 лет.

9) Четыре кошки и 3 котенка весят 15 килограммов, а 3 кошки и 4 котенка весят 13 килограммов.
Предполагается, что все взрослые кошки весят одинаково и котята также весят одинаково.
Сколько весит каждая кошка и каждый котенок в отдельности?

           Ответ:      Кошка весит 3 килограмма, котенок – 1 килограмм.

10) На чашечных весах 3 кубика и 1 морская раковина уравновешиваются 12 бусинами, а 1 раковина уравновешивается 1 кубиком и 8 бусинами.
Сколько бусин надо положить на свободную чашку весов, чтобы уравновесить раковину на другой чашке?

           Ответ:      Надо положить 9 бусин.

11) Три яблока и 1 груша весят столько же, сколько 10 персиков, а 6 персиков и 1 яблоко весят столько же, сколько 1 груша.
Сколько же персиков надо взять, чтобы уравновесить 1 грушу?

           Ответ:      Надо взять 7 персиков.

12) В Древнем Риме философы-законники любили задавать друг другу такую задачу.
Вдова обязана оставшееся после мужа наследство в 3500 золотых разделить с ребенком, который должен родиться.
Если это будет сын, то мать по римским законам получает половину сыновней доли.
Если родится дочь, то мать получает двойную долю дочери.
Но случилось так, что родились близнецы – сын и дочь.
Как следует разделить наследство, чтобы были выполнены все требования закона?

           Ответ:      Вдова должна получить 1000 золотых, сын – 2000 золотых, дочь – 500 золотых. Тогда требования закона будут выполнены, потому что вдова получит вдвое меньше сына и вдвое больше дочери.

13) Напишите по порядку девять цифр: 1 2 3 4 5 6 7 8 9.
Сможете ли вы, не меняя порядка цифр, вставить между ними знаки плюс и минус таким образом,
чтобы в результате получилось ровно 100?

           Ответ:      123 - 45 - 67 + 89 = 100.

14) В вашем распоряжении пять двоек и любые знаки математических операций.
Вы должны с помощью только этого цифрового материала, используя его полностью и применяя знаки математических операций,
выразить числа 15, 11, 12321.

Решение:      (2 + 2)² - 2/2 = 15
(2 * 2)² - 2/2 = 15
2^{2 + 2} - 2/2 = 15
22/2 + 2 * 2 = 15
22/2 + 2² = 15
22/2 + 2 + 2 = 15
22/2 + 2 - 2 = 11
(222/2)² = 111² = 12321.

15) Вы, конечно, знаете, что пятью тройками и знаками математических операций можно записать число 100: 33 - 3 + 3/3 = 100.
Но можно ли записать пятью тройками число 10?

Решение:      33/3 - 3/3 = 10
(3*3*3 + 3)/3 = 10
3³/3 + 3/3 = 10.

Смотрят на слайд, внимательно слушают задачу.

Отвечают на вопросы учителя, анализируя задачу, рассуждают.

Отвечают на вопрос.

Слушают задание.

Находят соседей, проверяют по слайду, исправляют ошибки.

Поднимают руки, вспоминают, что такое задачи, формируют группы, записывают ответ, делятся мыслями, рассуждают, выбирают выступающего, проверяют по слайду.

Сомооценка и взаимооценка.

Выполняют упражнения

Закрепление основного содержания внеурочного занятия.

Коммуникативные, познавательные УУД.

- А сейчас, ребята, я раздам каждому карточки. Вам нужно решить задачу самостоятельно

КАРТОЧКИ

- А теперь, давайте поработаем индивидуально, я раздам задачи, а вы их будуте роешать, а потом мы проверим.

ЗАДАЧА 1.

Известный бизнесмен Андрей Крутой пришел в Госбанк, чтобы обменять несколько 50- и 100- долларовых купюр старого образца.
Ему было выдано 1999 купюр достоинством 1, 5 и 25 долларов.
Докажите, что его обсчитали. 

ЗАДАЧА 2.

Три землекопа за два часа выкопали три ямы.
Сколько ям выкопают шесть землекопов за пять часов? 

ЗАДАЧА 3.

Кот Матроскин и пес Шарик каждое утро бегают на речку умываться. Они выскакивают из дома одновременно и бегут по одной и той же тропинке. Скорость каждого из них постоянна, но Матроскин бежит в 3 раза быстрее Шарика, зато моется в 2 раза дольше, чем Шарик. Однажды Шарик, прибежав к речке, обнаружил, что не взял с собой полотенце. Он тут же побежал домой, схватил полотенце и прибежал к речке как раз в тот момент, когда Матроскин закончил умываться (бежал Шарик по той же тропинке и с той же скоростью, что и каждое утро).
Кто обычно прибегает домой раньше – Шарик или Матроскин или они прибегают домой одновременно? 

ЗАДАЧА 4.

В Цветочном городе живет 14 коротышек. Они объединены в различные партии. По закону, партия должна состоять не менее чем из 3 коротышек, и две разные партии не могут состоять из одних и тех же членов. Кроме того, каждый коротышка может быть членом не более 2 партий.
Какое наибольшее число партий может быть в Цветочном городе? 

ЗАДАЧА 5.

Во время шторма капитан корабля приказал выбросить за борт половину из 30 тюков с товарами, которые везли два купца. Купцы были в нерешительности: каждому было жаль выбрасывать свой груз. Видя это, капитан сказал: «Сделаем так: матросы расставят 30 тюков по кругу, а мы будем по кругу ходить и выбрасывать каждый девятый тюк, пока не выбросим половину тюков». Один из купцов подкупил матросов, и они сумели расставить тюки так, что 15 оставшихся на палубе тюков оказались с товарами одного купца.
Как были расставлены тюки? 

ЗАДАЧА 6.

Футбольный мяч сшит из 32 лоскутков: белых шестиугольников и черных пятиугольников. Каждый черный лоскуток граничит только с белыми, а каждый белый - с тремя черными и тремя белыми. Сколько лоскутков белого цвета? 

ЗАДАЧА 7.

Инженер ежедневно приезжал на станцию в одно и то же время, и в то же время за ним подъезжала машина, на которой он ехал на завод. Однажды инженер приехал на станцию на 55 мин раньше обычного. Сразу пошел навстречу машине и приехал на завод на 10 мин раньше, чем обычно.
Во сколько раз скорость инженера меньше скорости машины? 

ЗАДАЧА 8.

В вагоне электропоезда ехали из города на дачу две подруги-школьницы. 
«Я замечаю, – сказала одна из подруг, – что обратные дачные поезда нам встречаются через каждые 5 мин. Как ты думаешь, сколько дачных поездов прибывает в город в течение одного часа, если скорости поездов в обоих направлениях одинаковы?» «Конечно, 12, так как 60 : 5 = 12», – сказала вторая подруга. Но школьница, задавшая вопрос, не согласилась с решением подруги и привела ей свои соображения. А что вы думаете по этому поводу? 

ЗАДАЧА 9.

В триседьмом царстве живут драконы. У каждого дракона одна, две или три головы,
а) Может ли у 40 % драконов быть 60 % голов?
б) Может ли у 40 % драконов быть 70 % голов? 

РЕШЕНИЯ ЗАДАЧ.

Решение задачи 1.

Для решения этой задачи необходимо воспользоваться следующим известным утверждением: сумма любого числа четных чисел – четная, а нечетного числа нечетных чисел – нечетная. В нашем случае исходная сумма денег (сумма какого-то числа 50-долларовых и 100-долларовых купюр) – четная, а полученная сумма денег (сумма 1999 купюр по 1, 5 и 25 долларов) – нечетная. 

Решение задачи 2.

Шесть землекопов за 2 часа выкопают 3 · 2 = 6 ям. Шесть землекопов за 10 часов выкопают 6·5=30 ям. Тогда шесть землекопов за 5 часов выкопают 30 : 2 = 15 ям. 

Решение задачи 3.

Разделим дорогу от дома к речке на три участка одинаковой длины (см. рисунок) и эту длину примем за 1.

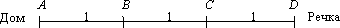
Введем новую единицу измерения – «шарик»; по определению, 1 «шарик» – это время, нужное Шарику, чтобы утром по дороге на речку пробежать участок длины 1. 
По условию, когда Матроскин добегает до D (начинает умываться), Шарик как раз находится в точке B (ведь он бежит в 3 раза медленнее Матроскина). Следовательно, на дорогу от дома до речки (так же, как и на обратную дорогу) Матроскин затрачивает столько же времени, сколько нужно Шарику, чтобы пробежать отрезок длины 1, т. е. 1 «шарик». 
Матроскин умывается 8 «шариков» (действительно, в тот день, когда Шарик забыл полотенце, он, как всегда, добежал до точки B, а Матроскин в этот момент начал умываться, затем Шарик пробежал 8 раз отрезок длины 1: от B к D (два участка длины 1), от D к A(три участка длины 1) и, наконец, от A к D уже с полотенцем (три участка длины 1), - и как раз Матроскин в этот момент умываться закончил). Далее, так как по условию Матроскин моется в два раза дольше Шарика, то Шарик моется 4 «шарика». 
Остается подсчитать время, затраченное каждым из наших героев на дорогу от дома к речке, умывание и дорогу обратно, от речки к дому. Шарик: 3 + 4 + 3 = 10 «шариков»; Матроскин: 1 + 8 + 1 = 10 «шариков».
Следовательно, Матроскин и Шарик прибегают домой после умывания одновременно. 

Решение задачи 4.

Пусть в каждой партии выдают партийные билеты. Если в цветочном городе k партий, то на руках у населения не менее 3k партийных билетов (ведь в каждой партии по условию не менее 3-х членов). Но у каждого коротышки имеется не более 2-х партийных билетов (по условию каждый коротышка не может быть членом более 2-х партий). Следовательно, так как коротышек 14, всего партийных билетов не более 2 x 14 = 28 . 
Поэтому 3k Остается привести пример вхождения 14 коротышек в 9 партий такой, чтобы: 
1) в каждой партии было не меньше 3 членов; 
2) каждый коротышка являлся бы членом не более 2-х партий; 
3) никакие две разные партии не состоят из одних и тех же членов (при выводе оценки k Пронумеруем коротышек числами от 1 до 14. Условимся коротышек, входящих в какую-либо партию, заключать в фигурные скобки {}. Нужный пример иллюстрируют, например, партии: {1,2,3}, {4,5,6}, {7,8,9}, {10,11,12}, {13,14,1}, {2,3,4}, {5,6,7}, {8,9,10}, {11,12,13}. 
Всего 9 партий. 

Решение задачи 5.

Начертим круг, отметим на нем 30 палочек и пронумеруем их от 1 до 30. Начиная счет с цифры 1, перечеркиваем девятую палочку, затем восемнадцатую, затем двадцать седьмую и продолжаем этот процесс, вычеркивая каждую девятую из не перечеркнутых ранее палочек. Таким образом, будут перечеркнуты палочки с номерами 5, 6, 7, 8, 9, 12, 16, 18, 19, 22, 23, 24, 26, 27, 30. Значит, купец просил матросов расставить тюки следующим образом: 4 своих, 5 чужих, 2 своих, 1 чужой, 3 своих, 1 чужой, 1 свой, 2 чужих, 2 своих, 3 чужих, 1 свой, 2 чужих, 2 своих, 1 чужой. 

Решение задачи 6.

Обозначим искомое число лоскутков белого цвета через x. Тогда лоскутков черного цвета будет 32 - x. Чтобы составить уравнение, подсчитаем двумя способами количество границ белых лоскутков с черными. Каждый белый лоскут граничит с тремя черными, следовательно, число границ равно 3x. С другой стороны, каждый черный лоскут граничит с пятью белыми и число границ равно 5(32 – х). Получаем уравнение 3x = 5(32 – х), т.е. 8х = 160 и х = 20. 

Решение задачи 7.

За 10 мин машина проходит путь, равный двойному расстоянию от станции до места встречи инженера с машиной. Значит, путь от станции до места встречи машина проходит за 5 мин. На месте встречи машина была за 5 мин до времени обычного приезда инженера на станцию, значит, путь от станции до места встречи инженер шел 55 мин - 5 мин = 50 мин. Следовательно, скорость инженера в 50 : 5 = 10 раз меньше скорости машины. 

Решение задачи 8.

Скорости поездов одинаковы, поэтому за одно и тоже время они проходят одно и тоже расстояние. Из сказанного выше следует, что в город прибудут в течение одного часа только дачные поезда встречающиеся в первой половине часа (30 минут), а дачные поезда встречающиеся во второй половине часа не будут успевать доходить до города за оставшееся время. 
Значит, в течение одного часа в город прибывает 30 : 5 = 6 дачных поездов. 

Решение задачи 9.

а) Покажем, что у 40% драконов может быть 60% голов. Пусть в этом царстве живет 100 драконов: 40 драконов с одной головой, 20 – с двумя головами и 40 – с тремя. Тогда число голов у всех драконов равно 40 • 1 + 20 • 2 + 40 • 3 = 200. При этом все 40 трехглавых драконов, что составляет 40% от общего числа драконов, имеют 40 • 3 = 120 голов, что составляет 120/200 • 100% = 60% от общего числа голов. 
б) Пусть число драконов равно х, а общее число голов у них равно у. Предположим, что какие-то 40% драконов имеют 70% голов. Тогда, поскольку каждый из этих драконов имеет не более трех голов, то 0,7у

Подводятся итоги команд. Делается анализ.

Выполняют задание индивидуально, размышляют, вспоминают, анализируют.

Проверяют по слайду, оценивают работу соседа.

Рефлексия.

Личностные, регулятивные УУД.

- Найдите на партах разноцветные листочки. Мы сейчас проведем этап урока рефлексия под названием : «Мясорубка». Красные листочки означают, что вы сегодня ничего из урока для себя интересного не получили, желтые, что вам что-то понравилось, а зеленые, вам понравилось все. Приклейте, пожалуйста, на доску соответствующие цвета – цвета вашего настроения.

Ученики приклеивают на доску.