ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ГОРОДА МОСКВЫ «ШКОЛА №2036»
Разработка урока по математике на тему
«Решение задач на движение»
6 класс
Автор:
учитель математики
Панченко Елена Николаевна
Тема урока: Решение задач на движение.
Цели учителя:
создание условий для осознанного и уверенного владения навыком решения задач на движение.
Образовательные задачи урока:
отработать навыки записи правил для вычисления скорости, времени и расстояния в виде формул и их применения при решении задач на движение;
закрепить навык представления информации, заданной в условии задачи в виде алгебраических выражений;
отработать навык представления условия задачи в виде схемы и составления задачи по информации, представленной на схеме;
закрепить навыки решения задач на движение арифметическим способом, а так же, используя три этапа математического моделирования.
Развивающие задачи урока:
развивать творческие способности учащихся; умение обобщать, классифицировать, строить умозаключения, делать выводы; коммуникативные навыки; умение сотрудничать при решении учебных задач.
Воспитательные задачи урока:
воспитывать культуру умственного труда; культуру коллективной работы; упорство в достижении цели.
Цели учащегося:
- полное понимание сути решения задач на движение арифметическим способом, а так же с помощью уравнений;
- осознанный и вдумчивый подход к анализу условий задач и отбору этих условий для связи между неизвестными величинами и для составления уравнений, а также понимание необходимости и достаточности количества этих условий для единственности решения;
- приобщение их к процессу творчества, открытия для себя нового;
- осознание чувства сопричастности к общему успеху.
Тип урока: урок решения задач.
Оборудование: компьютер, экран, проектор.
Ход урока.
Устная работа.
1.Беседа с учащимися.
Учитель. Ребята!
- Как вы считаете? Зачем нам нужно уметь решать задачи на движение?
(чтобы не опаздывать на встречи, уметь спланировать время выхода, рассчитать скорость движения, чтобы не было аварий, и т.д.)
2. Опрос учащихся.
Какие 3 взаимосвязанные величины рассматриваются в задачах на движение?
- В каких единицах измеряется скорость, время, расстояние?
- Какими буквами обозначаются скорость, время, расстояние?
S - расстояние (пройденный путь),
t - время движения и
V - скорость – расстояние, пройденное за единицу времени.
- Как найти расстояние, зная скорость и время? Запишите соответствующую формулу. S = V t
- Как найти скорость, зная расстояние и время? Запишите соответствующую формулу. V = S / t
- Как найти время, зная расстояние и скорость? Запишите соответствующую формулу. t = S / V.
3. Задание №1. Автобус едет со скоростью х км/ч, автомобиль – на 20км/ч быстрее.
1) Что означает выражение:
а) х+25; б) 3х; в) 2(х+25).
2) Что означает равенство:
а) 3х=2(х+20); б) 3х+5=2(х+25); в) 3х=2(х+25)+12.
Практическая работа.
Задание №2. (Задание с взаимопроверкой)
Автомобиль едет со скоростью х км/ч, а автобус на 20 км/ч медленнее. Составьте выражения для следующих величин:
а) скорость автобуса;
б) расстояние, пройденное автомобилем за 3 часа;
в) расстояние, пройденное автобусом за 4 часа;
Составьте уравнения, зная, что
г) автомобиль за 3 часа прошёл тоже расстояние, что и автобус за 4 часа;
д) автомобиль за 3 часа прошёл расстояние на 15км больше, чем автобус за 3 часа.
Ответ: а) х-20; б) 3х; 4(х-20); г) 3х=4(х-20); д) 3х-4(х-20)=15.
Устная работа.
Посмотрите на данные схемы. Какие могут быть ситуации в задачах на движение?
Составьте задачу для каждой из представленных на слайде схем и решите её.
Ситуация первая. (Встречное движение).
Два объекта движение начинают одновременно навстречу друг другу.
Как найти скорость сближения?
Рис.1. (Слайд №4)
Ситуация вторая. (Движение в противоположных направлениях из одного пункта).
Два объекта движение начинают одновременно в противоположных направлениях.
Как найти скорость удаления?
Рис.2 (Слайд №5)
Ситуация третья. (Два объекта движение начинают одновременно в одном направлении).
Как найти скорости сближения и удаления?
Рис.3 (Слайд №6)
Задание №3. Из двух городов, расстояние между которыми 162 км, одновременно навстречу друг другу выехали два велосипедиста. Скорость одного на 3 км/ч больше скорости другого. Встреча произошла через 6ч после их выезда. С какой скоростью ехал каждый велосипедист?
1. Представить условие задачи в виде схемы и решить задачу арифметическим способом.
Решение.
1. 162:6=27(км/ч) – скорость сближения.
2. 27-3=24(км/ч) – 2 скорости 2 велосипедиста.
3. 24:2=12(км/ч) – скорость 2 велосипедиста.
4. 12+3=15(км./ч) скорость 1 велосипедиста.
Ответ: 12, 15.
2.Представить условие задачи в виде таблицы и решить задачу с помощью уравнения.
Решение.
6х+6(х+3)=162; х=12; 12+3=15.
Ответ: 12, 15.
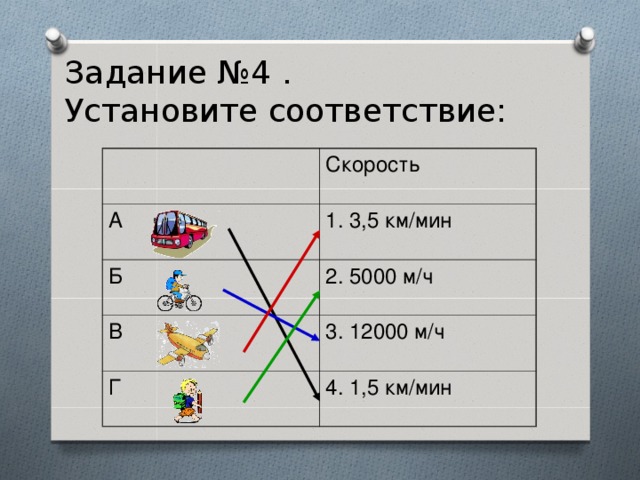
Задание № 4.
Установите в данной таблице соответствие:
А. Автобус 1. 3,5 км/мин
Б. Велосипедист 2. 5000 м/ч
В. Самолёт 3. 12000 м/ч
Г. Пешеход 4. 1,5 км/мин
Ответ:
А-4, Б-3, В-1, Г-2.
Задание №5. Решая задачу на движение, ученик при выполнении вычислений неправильно поставил запятую. У него получилось 83,55 м/мин. Какова на самом деле была скорость пешехода?
Ответ: 8,355 м/мин.
Домашнее задание: §20 №599, №607(а) (Учебник: Зубарев И.И. Математика 6 класс).
Итог урока (Беседа с учащимися)
- Что нам сегодня на уроке нам удалось повторить?
- Какие задания вам показались наиболее трудными?
- Какие задания показались вам самыми интересными?
Просмотр содержимого документа
«Разработка урока»
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГОРОДА МОСКВЫ
«ШКОЛА №2036»
Разработка урока по математике на тему
«Решение задач на движение»
6 класс
Автор:
учитель математики
Панченко Елена Николаевна
Москва 2015
Тема урока: Решение задач на движение.
Цели учителя:
создание условий для осознанного и уверенного владения навыком решения задач на движение.
Образовательные задачи урока:
отработать навыки записи правил для вычисления скорости, времени и расстояния в виде формул и их применения при решении задач на движение;
закрепить навык представления информации, заданной в условии задачи в виде алгебраических выражений;
отработать навык представления условия задачи в виде схемы и составления задачи по информации, представленной на схеме;
закрепить навыки решения задач на движение арифметическим способом, а так же, используя три этапа математического моделирования.
Развивающие задачи урока:
развивать творческие способности учащихся; умение обобщать, классифицировать, строить умозаключения, делать выводы; коммуникативные навыки; умение сотрудничать при решении учебных задач.
Воспитательные задачи урока:
воспитывать культуру умственного труда; культуру коллективной работы; упорство в достижении цели.
Цели учащегося:
полное понимание сути решения задач на движение арифметическим способом, а так же с помощью уравнений;
осознанный и вдумчивый подход к анализу условий задач и отбору этих условий для связи между неизвестными величинами и для составления уравнений, а также понимание необходимости и достаточности количества этих условий для единственности решения;
приобщение их к процессу творчества, открытия для себя нового;
осознание чувства сопричастности к общему успеху.
Тип урока: урок решения задач.
Оборудование: компьютер, экран, проектор.
Ход урока.
Устная работа.
Беседа с учащимися.
Учитель. Ребята!
- Как вы считаете? Зачем нам нужно уметь решать задачи на движение?
(чтобы не опаздывать на встречи, уметь спланировать время выхода, рассчитать скорость движения, чтобы не было аварий, и т.д.)
2. Опрос учащихся.
Какие 3 взаимосвязанные величины рассматриваются в задачах на движение?
В каких единицах измеряется скорость, время, расстояние?
Какими буквами обозначаются скорость, время, расстояние?
S - расстояние (пройденный путь),
t - время движения и
V - скорость – расстояние, пройденное за единицу времени.
Как найти расстояние, зная скорость и время? Запишите соответствующую формулу. S = V t
Как найти скорость, зная расстояние и время? Запишите соответствующую формулу. V = S / t
Как найти время, зная расстояние и скорость? Запишите соответствующую формулу. t = S / V.
3. Задание №1. Автобус едет со скоростью х км/ч, автомобиль – на 20км/ч быстрее.
1) Что означает выражение:
а) х+25; б) 3х; в) 2(х+25).
2) Что означает равенство:
а) 3х=2(х+20); б) 3х+5=2(х+25); в) 3х=2(х+25)+12.
Практическая работа.
Задание №2. (Задание с взаимопроверкой)
Автомобиль едет со скоростью х км/ч, а автобус на 20 км/ч медленнее. Составьте выражения для следующих величин:
а) скорость автобуса;
б) расстояние, пройденное автомобилем за 3 часа;
в) расстояние, пройденное автобусом за 4 часа;
Составьте уравнения, зная, что
г) автомобиль за 3 часа прошёл тоже расстояние, что и автобус за 4 часа;
д) автомобиль за 3 часа прошёл расстояние на 15км больше, чем автобус за 3 часа.
Ответ: а) х-20; б) 3х; 4(х-20); г) 3х=4(х-20); д) 3х-4(х-20)=15.
Устная работа.
Посмотрите на данные схемы. Какие могут быть ситуации в задачах на движение?
Составьте задачу для каждой из представленных на слайде схем и решите её.
Ситуация первая. (Встречное движение).
Два объекта движение начинают одновременно навстречу друг другу.
Как найти скорость сближения?
Рис.1. 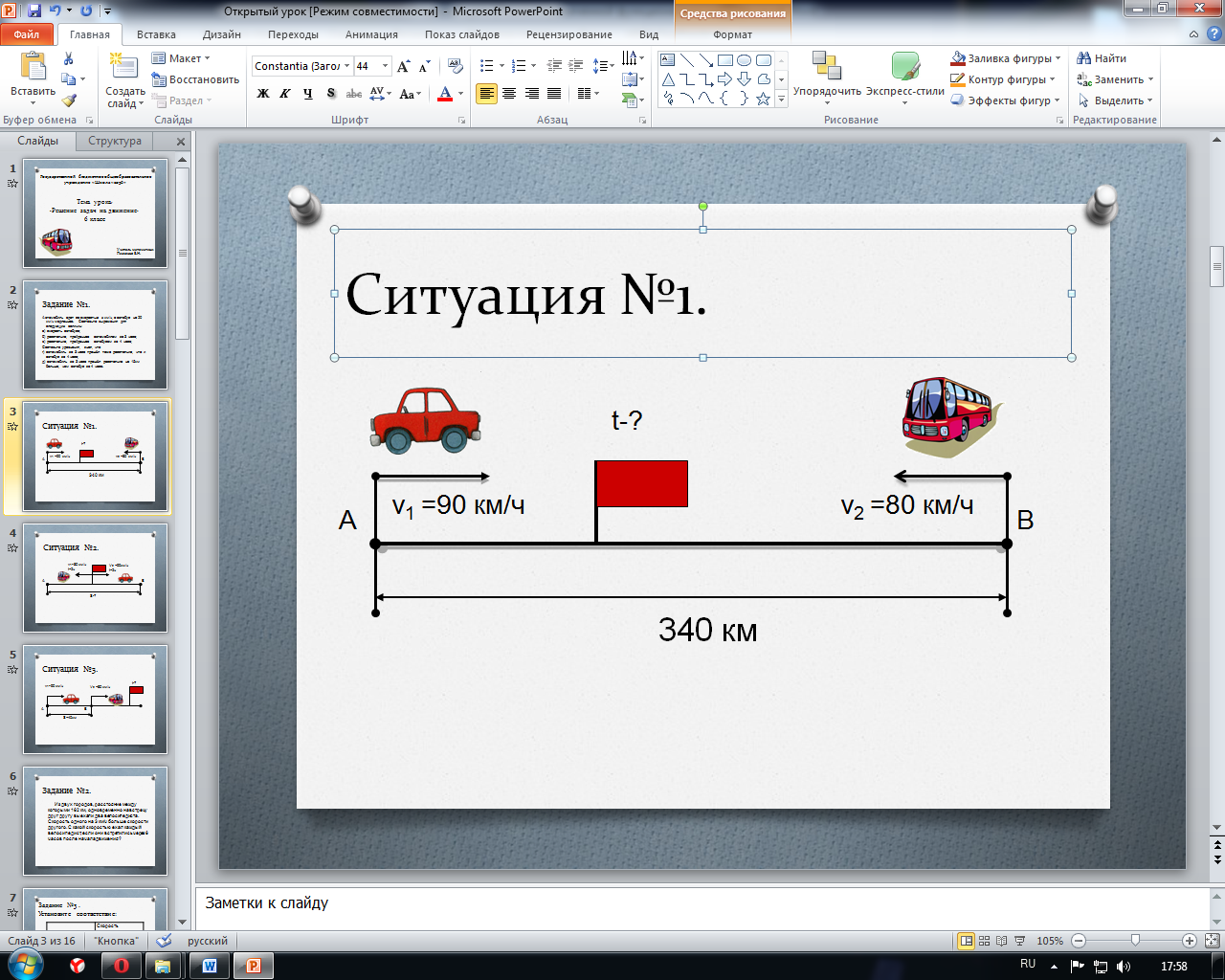
Ситуация вторая. (Движение в противоположных направлениях из одного пункта).
Два объекта движение начинают одновременно в противоположных направлениях.
Как найти скорость удаления?
Рис.2 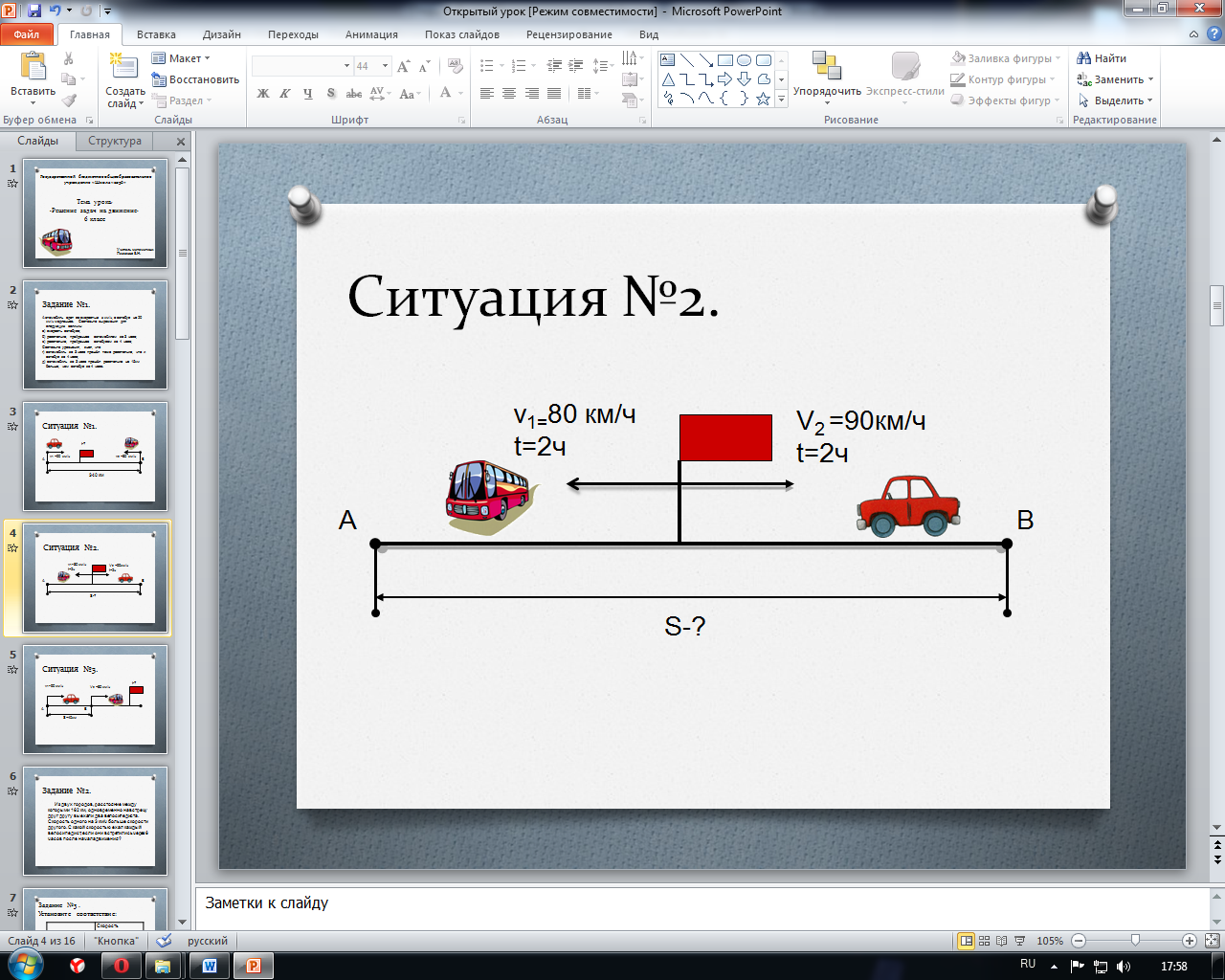
Ситуация третья. (Два объекта движение начинают одновременно в одном направлении).
Как найти скорости сближения и удаления?
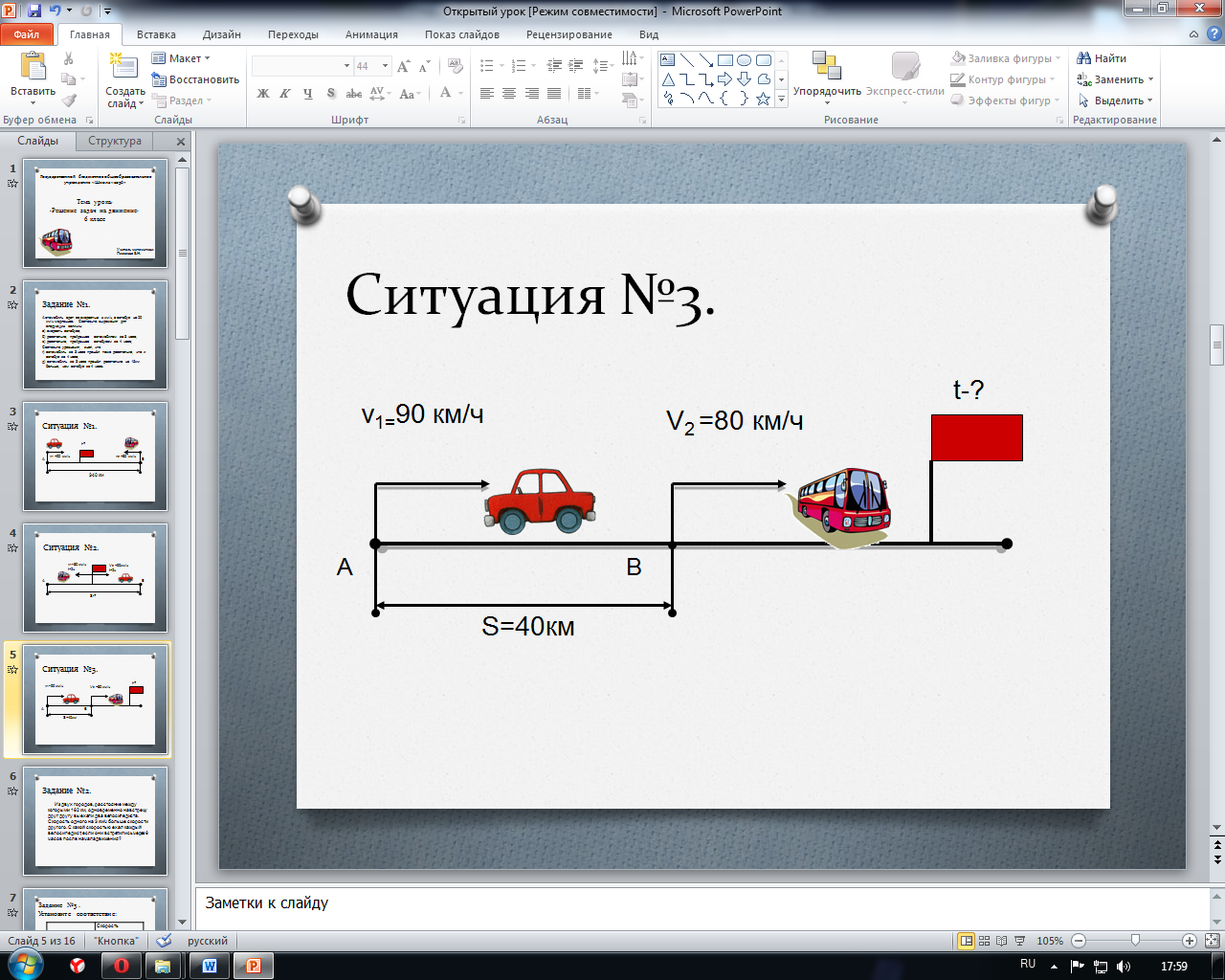
Рис.3
Задание №3. Из двух городов, расстояние между которыми 162 км, одновременно навстречу друг другу выехали два велосипедиста. Скорость одного на 3 км/ч больше скорости другого. Встреча произошла через 6ч после их выезда. С какой скоростью ехал каждый велосипедист?
1. Представить условие задачи в виде схемы и решить задачу арифметическим способом.
Решение.
1. 162:6=27(км/ч) – скорость сближения.
2. 27-3=24(км/ч) – 2 скорости 2 велосипедиста.
3. 24:2=12(км/ч) – скорость 2 велосипедиста.
4. 12+3=15(км./ч) скорость 1 велосипедиста.
Ответ: 12, 15.
2.Представить условие задачи в виде таблицы и решить задачу с помощью уравнения.
Решение.
|
| Скорость | Время | Расстояние |
| 1 | х+3 | 6 | 6(х+3) |
| 2 | х | 6 | 6х |
6х+6(х+3)=162; х=12; 12+3=15.
Ответ: 12, 15.
Задание № 4.
Установите в данной таблице соответствие:
| А. Автобус | 1. 3,5 км/мин |
| Б . Велосипедист | 2. 5000 м/ч |
| В. Самолёт | 3. 12000 м/ч |
| Г. Пешеход | 4. 1,5 км/мин |
Ответ:
Задание №5. Решая задачу на движение, ученик при выполнении вычислений неправильно поставил запятую. У него получилось 83,55 м/мин. Какова на самом деле была скорость пешехода?
Ответ: 8,355 м/мин.
Домашнее задание: §20 №599, №607(а) (Учебник: Зубарев И.И. Математика 6 класс).
Итог урока (Беседа с учащимися)
Что нам сегодня на уроке нам удалось повторить?
Какие задания вам показались наиболее трудными?
Какие задания показались вам самыми интересными?
Просмотр содержимого презентации
«Презентация»

Государственной бюджетное общеобразовательное учреждение города Москвы «Школа «2036»
Тема урока:
«Решение задач на движение»
6 класс
Учитель математики:
Панченко Е.Н.

Задание №1.
Автомобиль едет со скоростью х км/ч, а автобус на 25 км/ч медленнее.
1)Что означает выражение:
а) х-25;
б) 2х;
в) 3(х-25).
2) Что означает равенство:
а) 2х=3(х-25);
б) 2х+5=3(х-25);
в) 2х=3(х-25)+12.

Задание №2.
Автомобиль едет со скоростью х км/ч, а автобус на 20 км/ч медленнее. Составьте выражения для следующих величин:
а) скорость автобуса;
б) расстояние, пройденное автомобилем за 3 часа;
в) расстояние, пройденное автобусом за 4 часа;
Составьте уравнения, зная, что
г) автомобиль за 3 часа прошёл тоже расстояние, что и автобус за 4 часа;
д) автомобиль за 3 часа прошёл расстояние на 15км больше, чем автобус за 4 часа.
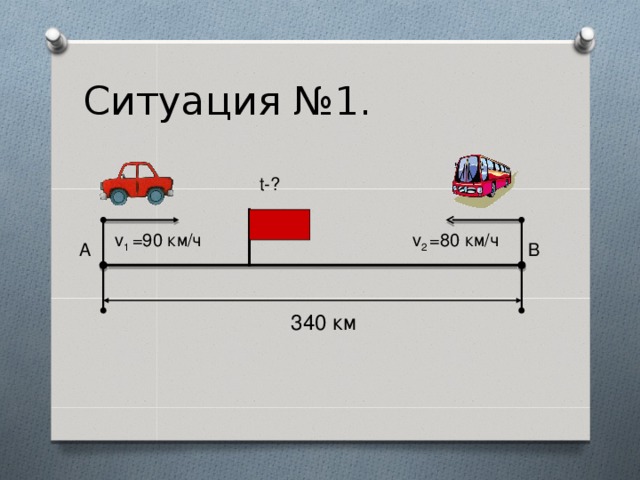
Ситуация №1.
t-?
v 2 =80 км/ч
v 1 =90 км/ч
А
В
340 км
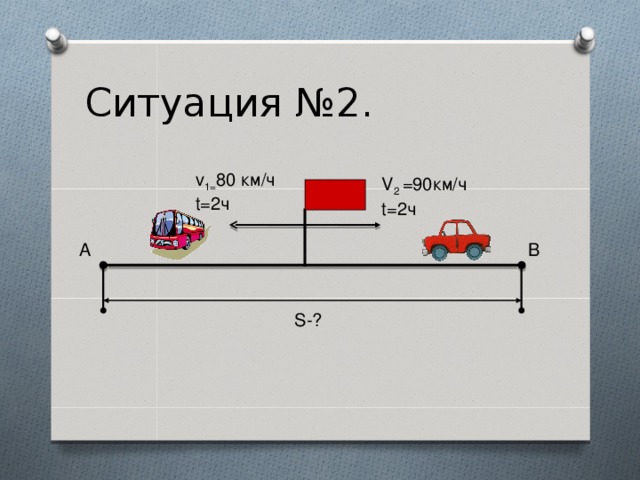
Ситуация №2.
v 1= 80 км/ч
t=2ч
V 2 =90км/ч
t=2ч
А
В
S-?
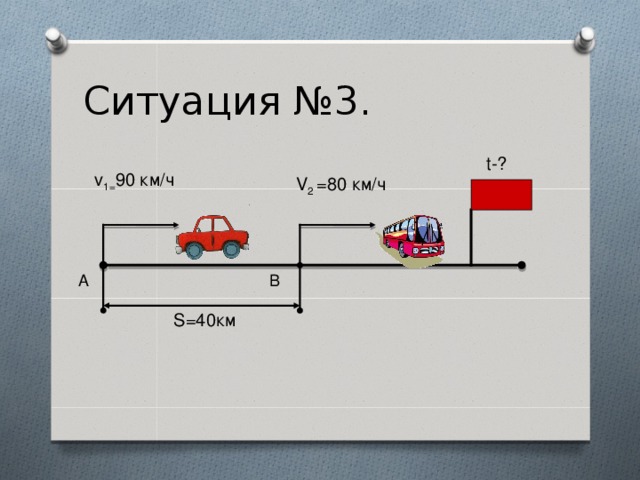
Ситуация №3.
t-?
v 1= 90 км/ч
V 2 =80 км/ч
А
В
S=40км

Задание №3.
Из двух городов, расстояние между которыми 162 км, одновременно навстречу друг другу выехали два велосипедиста. Скорость одного на 3 км/ч больше скорости другого. С какой скоростью ехал каждый велосипедист, если они встретились через 6 часов после начала движения?

Задание №4 . Установите соответствие:
Скорость
А
1. 3,5 км/мин
Б
2. 5000 м/ч
В
3. 12000 м/ч
Г
4. 1,5 км/мин
Задание №4 . Установите соответствие:
Скорость
А
1. 3,5 км/мин
Б
2. 5000 м/ч
В
3. 12000 м/ч
Г
4. 1,5 км/мин

Задание №5.
Решая задачу на движение, ученик при выполнении вычислений неправильно поставил запятую. У него получилось 83,55 м/ин.
Какова на самом деле была скорость пешехода?

Домашнее задание
§20 Повторить три этапа математического моделирования.
№ 599, №607(а)

Спасибо за урок!































