Проект урока по теме «Площадь»
(5 класс, Виленкин Н.Я.)
Тема урока: Площадь.
Тип урока: изучение нового материала.
Цели урока:
| Обучающие: | Обеспечить восприятие, осмысление учащимися изучаемого материала о площади геометрических фигур через элементы исследовательской работы. Сформировать способность к решению задач на вычисление площадей фигур. |
| Развивающие: | Создать условия для развития у школьников навыков логического мышления через мини - исследования. Содействовать развитию внимания, речи учащихся через устные ответы на вопросы, правильно формулировать мысли, развить умение воспринимать устную речь, развить пространственную ориентацию. |
| Воспитательные: | Способствовать свободному самовыражению, толерантности, взаимопомощи в групповой работе. |
Данный урок является первым в изучении большой темы «Площадь». Урок важен в процессе обучения, поскольку имеет практическое применение, и необходим для последующих уроков изучения данной темы. Знание вычисления площади основных фигур, таких как квадрат, прямоугольник, поможет определить площади более сложных фигур. Знание вычисления площадей фигур пригодится учащимся в жизни, например, для построения каких-то предметов, на уроках труда. В начальных классах уже вводилось понятие площади квадрата и прямоугольника. В 5 классе данная тема разбирается основательнее, подробнее, с записью формул и свойств площадей фигур.
Урок построен на деятельностной основе, что даст возможность реализовать компетентностный подход. Акцент делается на обучение через практику, продуктивную работу учащихся в группах с использованием элементов исследовательской работы, что соответствует психологическим особенностям учащихся данного класса. Цели урока соответствуют содержанию материала, программным требованиям, определяются необходимым уровнем знаний и умений учащихся по теме «Площадь». При изучении темы учащиеся выведут основные свойства площадей геометрических фигур, научатся находить площади треугольника и трапеции, будет формироваться умение определять площади более сложных фигур, используя площадь квадрата и прямоугольника.
При проектирование урока используются такие педагогические технологии, как проблемное обучение, элементы исследовательской деятельности, ИКТ-технологии.
Формы организации деятельности: фронтальная, групповая, индивидуальная, парная.
Оборудование: Раздаточный материал (карточки с заданиями (задание 1, задание 2, задание 3) для исследовательской работы, карточки с тестом в двух вариантах на этапе закрепления материала, листы контроля знаний), модель домика для собачки, ИКТ-технологии.
Ход урока.
1. Организационный этап.
Данный этап носит психологический характер.
Мотивационный компонент учебной деятельности: социальная мотивация –
обеспечение рабочей и доброжелательной обстановки на уроке.
Метод обучения – объяснительный (слово учителя)
Форма организации учебной деятельности – фронтальная
─ Здравствуйте, ребята! Встали, выпрямились. Тихо сели. Проверьте, все ли у вас готово к уроку: тетрадь, ручка, карандаш, линейка, учебник, дневник. Проверили? Молодцы. Желаю вам успешной работы на уроке.
2. Вводный этап.
Мотивационный компонент учебной деятельности. Создание условий для организации
внимания учащихся. Здесь формируется умение себя мобилизовать, сосредоточиться,
внутренне организоваться.
Метод обучения – частично-поисковый
Форма организации учебной деятельности – фронтальная
Слайд 1.
Цитата: Природа говорит языком математики: буквы этого языка – прямоугольники, треугольники, круги и иные математические фигуры. Галилей Г.
─ Как вы понимаете смысл этого выражения? Приведите свои примеры.
(Все предметы в природе имеют форму различных геометрических фигур)
3. Актуализация знаний.
Актуализация знаний проводится через выполнение задания частично – поискового
характера. На данном этапе предполагается вспомнить ранее изученный материал и
плавно подвести учащихся к теме урока.
Операционный компонент учебной деятельности – сосредоточение внимания,
мыслительная работа.
Метод обучения: словесный.
Форма организации учебной деятельности: фронтальная.
Слайд 2. На слайде:







─ Как называются фигуры, изображенные на слайде?
(квадраты, прямоугольники, треугольники, четырехугольник)
─ Как по-другому называется последний четырехугольник?
Ребята, эта фигура называется трапецией.
Рассказать о происхождении слова трапеция я попросила заранее подготовить (ФИ ученика)
«Трапеция» происходит от латинского слова «трапезиум» – латинской формы
греческого слова «трапезион», что значит столик. От этого же корня происходит
наше слово «трапеза», означающее по-гречески стол.
─ Спасибо за сообщение.
─ Ребята, а чем отличаются фигуры друг от друга? (формой, размерами)
─ Что можно определить по размерам фигуры? (периметр, площадь)
4. Сообщение темы и мотивация учебной деятельности учащихся.
На этом этапе осуществляется совместная постановка целей урока, занимательность,
заинтересованность в получении новых знаний. На этом этапе развиваются коммуникативные умения, осуществляется взаимодействие учитель-ученик.
Мотивационный компонент учебной деятельности - познавательная мотивация:
совместная постановка целей урока; занимательность.
Метод обучения: словесный.
Форма организации учебной деятельности: фронтальная.
─ Тема нашего сегодняшнего урока «Площадь» (показать рукой на тему, написанную на
доске)
─ Откройте тетради. Запишите число, классная работа и тему урока: «Площадь»
─ Ребята, чему мы должны сегодня научиться?
(уметь находить площади различных геометрических фигур)
─ В каких единицах измеряется площадь? (в см2, дм2, м2)
─ Ребята, а в каких профессиях не обойтись без знания площади фигуры? Обоснуйте свой ответ.
5. Создание проблемной ситуации. Задание практико-ориентированной
направленности. Выдвижение гипотезы.
Данный этап разъясняет учащимся, для чего изучается тема урока, как ее применить на практике. На этом этапе учащиеся ищут пути решения поставленной перед ними проблемы. Выдвигают гипотезы.
Мотивационный компонент учебной деятельности – познавательная мотивация: заинтересованность в получении новых знаний.
Операционный компонент учебной деятельности – поиск путей решений проблемы, выдвижение гипотезы.
Метод обучения: наглядный, словесный, проблемный (создание проблемной ситуации,
выдвижение гипотезы).
Форма организации деятельности – фронтальная.
Средства обучения: картонная модель домика для собачки.
─ Чтобы, например, построить вот такой домик для собачки, что нам нужно определить?
(показать перед классом макет домика из картона, сделанный руками)

( Нам нужно определить площадь пола, площадь стенок, площадь отверстия…)
─ Ребята, а что нужно знать, чтобы вычислить площадь фигуры? (размеры фигуры)
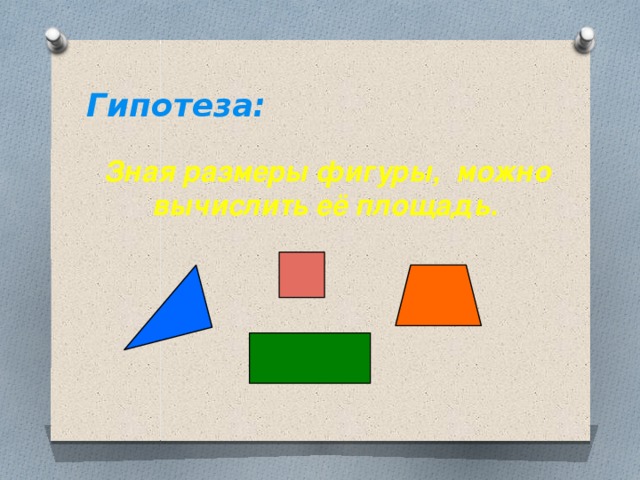
Итак, мы выдвинули гипотезу: Слайд 3.
Зная размеры фигуры, можно вычислить её площадь.
6. Проверка гипотезы, групповая работа.
На данном этапе обеспечивается восприятие, осмысление учащимися изучаемого материала через элементы исследовательской работы в группах. Создание условий для развития у школьников умений самостоятельно находить ответы на поставленные учителем вопросы. Формируются надпредметные умения: анализ, синтез, сравнение. Развиваются коммуникативные умения ученик – ученик при работе в группах, учитель – ученик при ответах на задания.
Мотивационный компонент учебной деятельности: осуществление познавательной мотивации через элементы исследовательской работы; Осуществление социальной мотивации через сотрудничество и взаимопомощь при работе в группах.
Операционный компонент учебной деятельности: мыслительные операции, анализирование, сравнение.
Регулирующий компонент учебной деятельности: работа в группе, контроль консультантами групп, наблюдения учителя.
Метод обучения: объяснительный, практический, исследовательский, контрольно-проверочный.
Форма организации учебной деятельности: групповая.
Средства обучения: карточки с заданиями исследовательского характера, листы контроля.
─ Проверим нашу гипотезу.
Для этого поработаем в группах. Разделимся на 6 групп. В каждой группе есть
консультант, который будет помогать мне и оценивать работу каждого члена группы.
─ Ребята, возьмите карточку с заданием 1, внимательно прочитайте его и начинайте
выполнять каждый самостоятельно. На это задание вам 2 мин.
Задание 1. (выдан набор геометрических фигур с определенными размерами)



4 6 3 6


4 3 6 5 4
5 7 10
1. Сравните данные вам фигуры.
2. Распределите их по форме.
3. Вычислите площадь этих фигур, зная их размеры.
4. Если есть фигуры, площадь которых вы определить не можете, отложите их.
─ Время вышло. Развернитесь в группах друг к другу.
Вам нужно:
1) обсудить задание, выполненное вами самостоятельно;
2) прийти к единому мнению;
3) быть готовыми защищать свою точку зрения
Ребята, вам на это 1 минута.
─ Итак, время вышло. Обсуждение завершили. Развернитесь на свои места.
─ Проверим, что получилось. Все ли мы пришли к одинаковому результату?
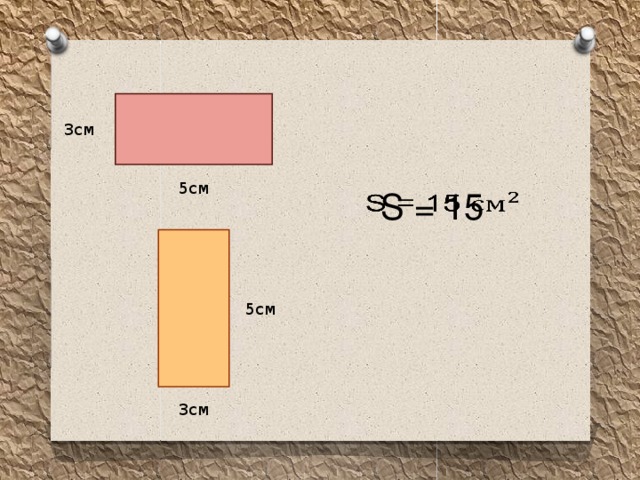
─ 3-я группа, нашли ли вы среди фигур равные? Что это за фигуры? Назовите их
площадь. (Среди фигур есть равные. Это прямоугольники. Их площадь равна 15 см2.)
─ Остальные группы, какой результат получили вы? (Отвечают)
─ Ребята, и я с вами согласна. Слайд 4. (показываю ответ на слайде)
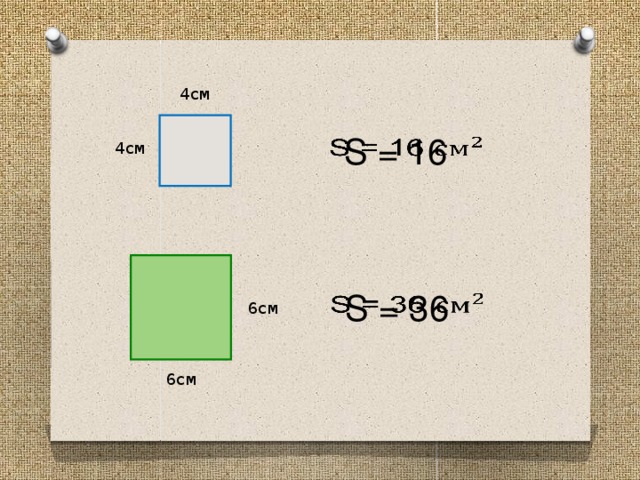
─ 2-ая группа, нашли ли вы среди фигур квадраты? И чему равна их площадь?
(Среди фигур есть 2 квадрата. Площадь одного из них = 16 см2, другого = 36 см2)
─ Остальные группы, а у вас чему равны площади квадратов? (Отвечают)
─ Верно, я с вами согласна. Слайд 5. (показываю ответ на слайде)
─ Консультанты групп, посмотрите на критерии и выставьте оценку каждому члену группы в
их оценочные листы.
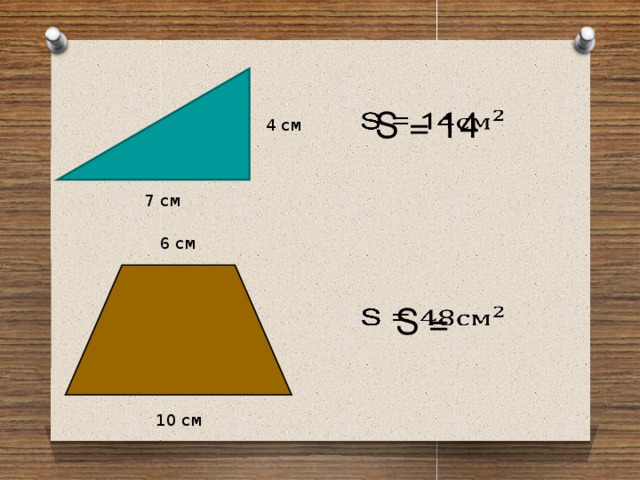
─ Консультанты групп поднимите руки, кто смог найти площадь треугольника.
─ Сверьте свои результаты с моими, у каких групп получилось также? (показываю свое
решение на слайде. Группы сравнивают ответы и называют их вариант) Слайд 6.
Дальше я рассчитываю, что учащиеся придут к неверному ответу, неправильно посчитают
площадь треугольника, что позволит провести дальнейшие исследования.
─ Ребята, вспомним нашу гипотезу. Верна ли она? (Частично)
Для всех ли фигур можно найти площадь, зная их размеры? (Не для всех).
─ А что это значит? ( Значит, нужны дополнительные расчеты.)
─ Проведем дальнейшее исследование, в ходе которого мы узнаем, как найти
площадь треугольника.
─ Ребята, объединитесь снова в прежние группы.
Возьмите карточки с заданием 2. Внимательно прочитайте алгоритм и попробуйте
выяснить, как найти площадь интересующей нас фигуры. Вам на выполнение 1 мин.
Задание 2.
Используя алгоритм, выясните, как найти площадь треугольника:
шаг 1. Достроить данный треугольник до прямоугольника.




+ =
шаг 2. Найти площадь полученного прямоугольника.
шаг 3. Разделить найденную площадь прямоугольника пополам.
шаг 4. Сделать вывод, чему равна площадь треугольника.
─ Время вышло. Развернитесь в группах друг к другу.
В течение 1 мин. вам нужно:
1) обсудить задание, выполненное вами самостоятельно;
2) прийти к единому мнению;
3) быть готовыми защищать свою точку зрения
─ Итак, обсуждение завершили. Развернитесь на свои места.
─ 4-ая группа, какой результат получился у вас? Объясните по шагам план ваших
действий. (Объясняют представители группы).
─ Остальные группы, а вы пришли к аналогичному результату? (Отвечают)
─ А какие из групп смогли найти площадь трапеции? (поднимают руки)
─ Сравните ваш результат с моим, пришли ли вы к такому ответу? (Показываю правильный ответ. Группы сравнивают ответы и называют их ответ.) Слайд 6.
В этой части работы я полагаю, что никто из учащихся не справится с этим заданием, что также позволит перейти к дальнейшим исследованиям.
─ Проведем дальнейшее исследование, в ходе которого мы узнаем, как найти площадь
трапеции.
─ Ребята, объединитесь снова в прежние группы.
Возьмите карточки с заданием 3. Внимательно прочитайте алгоритм и попробуйте
найти площадь трапеции. Вам на выполнение 1 мин.
Задание 3.
Используя алгоритм, выясните, как найти площадь трапеции:
![]()

![]()
шаг 1. Рассмотрите трапецию.
шаг 2. Назовите, из каких фигур она состоит?
шаг 3. Сделайте вывод, чему равна площадь трапеции.
шаг 4. Найдите площадь трапеции.
─ Время вышло. Развернитесь в группах друг к другу.
В течение 1 мин. вам нужно:
1) обсудить задание, выполненное вами самостоятельно;
2) прийти к единому мнению;
3) быть готовыми защищать свою точку зрения
─ Итак, обсуждение завершили. Развернитесь на свои места.
─ 5-ая группа, какой результат получился у вас? Объясните по шагам план ваших
действий. (Объясняют представители группы).
(Трапеция состоит из двух равных треугольников и квадрата. Поэтому, площадь трапеции равна сумме площадей двух треугольников и квадрата. Площадь треугольника равна 6 см2, площадь квадрата – 36 см2. Тогда площадь трапеции у нас получилась равной 48 см2 )
─ 6-ая группа пришли ли вы к верному ответу? (Отвечают)
─ Остальные группы, а у вас какой результат? (Отвечают)
─ Консультанты групп, посмотрите на критерии и выставьте оценку каждому члену
группы в их оценочные листы.
7. Вывод по результатам работы.
На данном этапе происходит анализ и обобщение полученных знаний по результатам исследовательской работы.
Операционный компонент учебной деятельности: анализ, обобщение полученных знаний.
Метод обучения: эвристический
Форма организации учебной деятельности: фронтальная.
─ Итак, ребята, сделаем вывод по результатам нашей работы.
─ Ответим правильно на гипотезу. Зная размеры фигуры, всегда ли можно определить
ее площадь? (учащиеся по результатам работы отвечают, что не всегда можно
определить площадь фигуры по ее размерам)
─ Давайте перечислим, что необходимо знать, вычисляя площадь геометрических фигур?
Учащиеся опираясь на выполненные задания перечисляют:
1. Равные фигуры имеют равные площади.
2. Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению длины на ширину.
3. Площадь всей фигуры равна сумме площадей ее частей.
─ Ребята, это называется свойствами геометрических фигур. Запишем их в виде формул.
Буква S – площадь фигуры, а стороны фигуры – буквы a, b. Тогда
справедливы формулы. Слайд 7.
8. Этап применения новых знаний в учебной деятельности.
Этап первичного закрепления новых знаний.
На данном этапе осуществляется перевод учащихся с этапа понимания на этап применения знаний. Учащиеся закрепляют знания и тренируют умения, полученные на уроке, выполняя задания из учебника.
Мотивационный компонент учебной деятельности: познавательная ситуация – применение новых знаний.
Операционный компонент учебной деятельности – письменная работа.
Регулирующий компонент учебной деятельности – самоконтроль.
Метод обучения: практический, частично-поисковый, контрольно-проверочный
Форма организации учебной деятельности: индивидуальная (каждый учащийся самостоятельно выполняет задание с последующей коллективной проверкой).
Средства обучения: учебник, листы контроля.
─ А теперь, изученное нами, применим на практике.
Откройте учебник на странице 110. Выполним номер №718.
─ Сережа, прочитай задачу.
№718. Ширина прямоугольника KNMT равна26 см, а его длина на 14 см
больше. Чему равна площадь прямоугольника KNMT? Чему равна
площадь каждого из треугольников, на которые разбивает отрезок KM
этот прямоугольник?
─ Я приглашаю тебя к доске (за разворот доски) решить эту задачу. Остальные
выполняют в тетради самостоятельно.
Ребята, вам на выполнение 3 мин.
─ 3 мин. прошло. Проверим, что получилось. Сережа, поверни твое решение.
Ребята, сравните результат.
№ 718: Дан прямоугольник KNMT.
N M


Схема к задаче: K T
Длина Ширина Площадь

![]()
![]()
26 см на 14 см ? см2
1) 26 + 14 = 40 см – ширина
2) S= 26*40 = 1040 см2 – площадь KNMT.
3) 1040 : 2 = 520 см2 – площадь треугольников KNM и MTK.
Ответ: 1040 см2, 520 см2.
─ Поднимите руки, у кого получился такой же ответ? Хорошо. У кого не так – сверьте и
найдите ошибки.
─ Ребята, есть вопросы по выполненным задачам? (Отвечают)
─ Теперь, возьмите свои оценочные листы, посмотрите на критерии и поставьте себе оценку
за работу с задачей.
─ Поднимите руки, у кого оценка 5? Молодцы! У кого 4?
9. Этап повторного закрепления новых знаний.
На этом этапе работы учащиеся вновь закрепляют полученные на уроке знания, выполняя
задания самостоятельно.
Мотивационный компонент учебной деятельности: познавательная ситуация – самостоятельное применение новых знаний.
Операционный компонент учебной деятельности – письменная работа.
Регулирующий компонент учебной деятельности – взаимоконтроль.
Метод обучения: частично-поисковый, контрольно-проверочный
Форма организации учебной деятельности: индивидуальная (каждый учащийся самостоятельно выполняет задание), парная (проверка задания осуществляется в парах, друг у друга).
Средства обучения: карточки с тестом в двух вариантах, листы контроля.
─ А сейчас, выполним в тетрадях небольшой тест на закрепление сегодняшнего материала.
Возьмите карточки с ТЕСТом (1вариант и 2вариант) и приступайте к его выполнению.
Ребята, вам на это 3 мин.
| Тест Вариант 1 1. Найдите площадь прямоугольника со сторонами 6 см, 4 см а) 10 см2; б) 24 см2; в) 2 см2; г) 20 см2. 2. Найдите площадь квадрата, сторона которого равна 11 см2. а) 120 см2; б) 22 см2; в) 121 см2; г) 200 см2. ![]()  ![]() 3. S1=5см2; S2=10см2; 3. S1=5см2; S2=10см2;
S1 S2 Чему равна площадь всей трапеции? а) 35см2; б) 20см2; в) 350см2; г) 200см2.  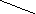 4. Чему равна площадь 4. Чему равна площадь
закрашенного треугольника? а) 42см2; б) 84см2; в) 19см2; г) 10см2. 5. Длина прямоугольника равна 52см2, ширина в 2 раза меньше. Чему равна ширина прямоугольника? а) 50 см; б) 104см; в) 54 см; г) 26 см.
| Тест Вариант 2. 1. Найдите площадь прямоугольника со сторонами 7 см, 3 см. а) 10 см2; б) 14 см2; в) 21 см2; г) 4 см2. 2. Найдите площадь квадрата, сторона которого равна 12 см2. а) 144 см2; б) 24 см2; в) 120 см2; г) 22 см2. ![]() ![]()  3. S1=6см2; S2=11см2; 3. S1=6см2; S2=11см2;
S1 S2 Чему равна площадь всей трапеции? а) 22см2; б) 9см2; в) 23см2; г) 24см2. 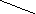  4. Чему равна площадь 4. Чему равна площадь
закрашенного треугольника? а) 19см2; б) 60см2; в) 11см2; г) 30см2. 5. Ширина прямоугольника равна 14см2, а длина в 3 раза больше. Чему равна длина прямоугольника? а) 42 см; б) 17 см; в) 11 см; г) 32 см.
|
─ Итак, ребята, 3 минуты прошло. Проверим тест.
Поменяйтесь тетрадями и проверьте друг у друга.
У вас должны получиться следующие варианты ответов. Слайд 8. (лист с ответами в
форме таблицы)
─ Согласно критерию поставьте друг другу оценку. Выставьте полученную оценку в ваш
оценочный лист.
─ Поднимите руки, у кого оценка 5? Молодцы! У кого 4? Хорошо.
10. Рефлексия, подведение итогов.
На данном этапе создаются условия для осознания учащимися содержания урока.
Происходит систематизация полученных на уроке знаний, определение оценки за урок.
Регулирующий компонент учебной деятельности.
Метод обучения: аналитический, оценочный
Форма организации учебной деятельности: фронтальная
Средства обучения: листы контроля, разноцветные геометрические фигуры, сделанные из бумаги для оценивания учащихся.
─ Ребята, подведем итоги сегодняшнего урока.
─ Что мы сегодня узнали на уроке и чем занимались?
(Узнали свойства площадей геометрических фигур. Закрепили умение находить площадь
прямоугольника и квадрата. Научились вычислять площади треугольника и трапеции)
─ Понравился вам сегодняшний урок?
─ Что нового вы для себя открыли сегодня на уроке?
─ Возьмите оценочные листы и по полученным оценкам поставьте себе оценку за урок.
─ Ребята, обратите внимание на фигуры, лежащие у каждого на столе: звездочка, квадрат и
треугольник.
─ Кто сегодня получил за урок оценку 5, поднимите звездочку; у кого оценка 4 – квадрат; у
кого оценка 3 – треугольник.
─ Сегодня на уроке хорошо работали, были активными (перечислить фамилии учащихся),
им я ставлю 5 в журнал.
Поставлю оценки отвечающим у доски. У остальных посмотрю тетради с классной
работой и оценочные листы.
11. Этап информации о домашнем задании и инструктаж по его выполнению.
На этом этапе учащимся произносится дифференцированное домашнее задание с
разъяснением по его выполнению.
─ Откройте дневники и запишите домашнее задание.
1 – пункт 18, №737(задача), №738(задача)
2 – пункт 18, №738(задача), №739(задача)
3 – пункт 18, №740(задача), Задание: найти площадь стен, пола и окон своей комнаты.
(Учащиеся слушают инструктаж о домашнем задании, записывают задание в дневник).
─ Урок закончен, спасибо за работу, можно идти на перемену.





















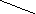 4. Чему равна площадь
4. Чему равна площадь