Признаки подобия треугольников. Решение задач.

Тип урока

Урок – практикум по решению задач

Цели урока для учителя

Воспитательные:

учить уважительно относиться друг к другу, корректно доносить свою позицию до других, принимать чужое мнение, учить строить диалог.

Развивающие:

развивать умения определения целей деятельности и составления плана действий, умение действовать согласно намеченному плану, соотносить результат своей деятельности с поставленной целью. Развивать умение организовывать самостоятельную деятельность; умения анализа и сравнения при решении схожих типов задач

Образовательные:

обобщить и систематизировать знания по теме: “Признаки подобия треугольников”; продолжить формирование навыков применения признаков подобия треугольников при решении задач, учить ориентироваться в своей системе знаний, выдвигать гипотезы решения проблемы.

Дидактические средства

Учебник, презентация, карточка с заданием, карточка- рейтинг

Оборудование

Компьютер, проектор, учебная доска

Обязательный минимум содержания

Понятия, правила, закономерности:

Определение подобных треугольников, признаки подобных треугольников.

Предметные умения:

Чтение чертежа, отбор нужной информации.

Практические задания:

Учебник

Дополнительные

П. 14.1 – 14.4(повторить)

Карточка

№ /№п/п

Этап Этапы урока

Деятельность учителя

Деятельность учащихся

Время

1

Организационная часть

. Обучающиеся рассажены группами по 4 человека. Здравствуйте, ребята! садитесь

Ребята, начнем наш урок с допуска к практикуму вытащите по билетику. Некоторые билеты могут содержать один и тот же вопрос. Но при ответе повторяться нельзя.

Итак, допуск сдан.

Откройте, пожалуйста, ваши тетради по подготовке к экзамену, запишите число.

Сегодня 14 декабря.

Откройте пособие по подготовке к ОГЭ

группа №1 – на стр. 16;

группа №2 - на стр. 94;

группа №3 – на стр. 218. Найдите задание № 13

Как вы знаете, на занятиях по подготовке к экзамену мы были вынуждены эти задачи пропустить. Почему?

Сможете ли вы сегодня решить возникающие проблемные ситуации на прошлых занятиях?

Если да, то почему?

Какая работа для этого нами была проделана?

Верно.

А как вы считаете, чем мы будем заниматься сегодня?

Верно. Давйтес формулируем тему урока.

Молодцы. Запишите тему в тетрадь.

Записать на доске

Какие задачи мы поставим перед собой сегодня на уроке?

Хорошо. Сегодня мы работаем в группах, поэтому можем поставить перед собой ещё несколько задач. Какие?

Тащат билеты.

Дают ответ на теоретический вопрос. (Если не знает, спасает группа)

.

Возможные варианты ответов

Эти задачи были пропущены, так как не был изучен необходимый теоретический материал.

Сможем, так как мы выяснили, какие треугольники называются подобными

Сформулировали и доказали признаки подобных треугольников, следствия из этих теорем, лемму о подобии треугольников.

Сегодня будем решать задачи на применение признаков подобия треугольников, следствий из них.

Тема урока «Признаки подобия треугольника. Решение задач»

Совершенствовать навыки в решении задач, учиться читать чертеж, отбирать нужный теоретический материал. Подготовиться к сдаче экзамена по математике.

Учиться слушать других.

Корректно отстаивать свою точку зрения, уважать мнение других.

Учиться выстраивать диалог.

5 мин

2

Актуализация знаний

Всё верно.

Но прежде, чем приступить к решению составбте план по выходу из проблемной ситуации. Как будем работать с предложенными задачами?

Какие будут предложения?

Молодцы. Будем придерживаться намеченного плана.

Вернитесь к заданию № 13, в течение минуты обсудите в группе решение.

Слушаем представителей групп

Группа 1.

Группа 2.

Группа 3.

Прочитать задачу.

Подтвердить или опровергнуть выдвинутые в задаче гипотезы, указав на соответствующую теорему или сформулировать верные доказанные утверждения.

Выбрать правильный ответ.

Группа 1

Какие из следующих утверждений верны?

1) Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключённые между ними равны, то треугольники подобны.

2) Сумма углов треугольника равна 360º.

3) Биссектриса равнобедренного треугольника, проведённая из его вершины к основанию, является его медианой.

Ответ: 13

Обоснование:

первое утверждение верно, так как это второй признак подобия треугольников.

Второе утверждение неверно, так как сумма углов треугольника равна 180º.

Третье – верно, так как это свойство биссектрисы равнобедренного треугольника.

Группа 2

Какие из следующих утверждений верны?

1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2) Любые два равносторонних треугольника подобны.

3) Все равнобедренные треугольники подобны.

Ответ:12

Обоснование:

первое утверждение – это первый признак подобия треугольников.

Второе утверждение верно, так как является следствием из первого признака подобия треугольников.

Третье неверное. Верное утверждение формулируется так: равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании (следствием из первого признака подобия треугольников).

Группа 3

Какие из следующих утверждений верны?

1) Если угол одного треугольника равен углу другого треугольника, то такие треугольники подобны.

2) Любые два равносторонние треугольники подобны.

3) Все прямоугольные треугольники подобны.

Ответ: 2

Обоснование:

Первое утверждение неверно. Первый признак подобия треугольников формулируется так: два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.

Второе утверждение верно, так как является следствием из первого признака подобия треугольников.

Третье неверно. Верное формулируется так:: прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.

10 мин

3

Мотивация познавательной деятельности.

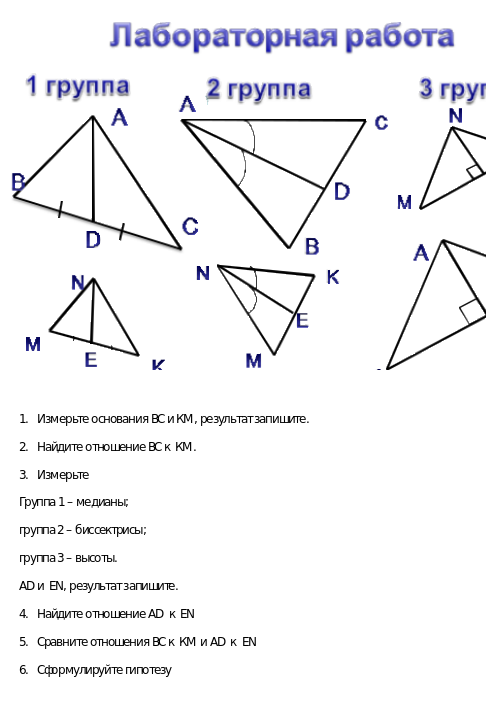
Ребята, мы много открытий для себя сделали в теме подобные треугольники. Но всегда интересно проводить эксперименты. Особенно важен конечный результат. Проведём лабораторную работу, которая поможет нам сделать научное открытие, упрощающее решение многих задач.

На рабочем столе у каждой группы лежат рабочие листы с печатной основой. Они содержат инструкцию.

Распределите работу в группах.

Следуйте указаниям чётко и быстро, и тогда у вас обязательно всё получится.

А мы ждём вашего открытия.

На эту работу отведём 7 минут.

Итак, закончили свои изыскания, что интересного открыла группа 1;

группа 2;

группа3?

Молодцы. Чему же равны все найденные вами отношения?

Я поздравляю, сейчас каждый открыл для себя новое свойство подобных треугольников.

Стороны треугольника, его медианы, биссектрисы, высоты называют линейными элементами треугольника.

Давайте, попробуем обобщить наши выводы.

Ребята, каждый из вас понимает, что сегодня мы сформулировали утверждение, которое нужно доказать.

Доказательством полученного результаты вы займётесь дома при решении задачи № 19. Это позволит получить высокую отметку за домашнюю работу.

.

.

Группа 1.

Отношение оснований подобных треугольников равно отношению медиан.

Группа 2.

Отношение оснований подобных треугольников равно отношению высот.

Группа 3

Отношение оснований подобных треугольников равно отношению высот.

Все отношения были равны коэффициенту подобия.

Обобщает наши результаты следующий вывод: в подобных треугольниках отношение сходственных линейных элементов равно коэффициенту подобия

10мин

4

Организация познавательной деятельности

А сегодня наша задача убедиться в том, что данное открытие приводит к устному решению задач модуля «Реальная математика»

Группа 1 - .№17 стр. 81;

группа 2 - №17 стр. 219;

группа 3 – карточка

Посмотрите предложенные вам задачи, составьте план вашей деятельности. На составление плана отведём минуту.

Через минуту.

Кто готов озвучить план?

Засекается три минуты на применение плана при решении задачи.

Если останется время

Ребята вы показали неплохие результаты при решении задач базового уровня. Давайте попробуем разобраться с задачей второй части экзаменационной работы

Задача второй части

№ 25 стр. 18

Постарайтесь справиться самостоятельно. В случае возникновении проблем, можно обращаться за помощью к представителям групп.

Если справились, то самопроверка.

Если правильно, то + на полях, и отметка «5» - в дневник.

Если не . Я рада, что мне удалось, в очередной раз создать проблемную ситуацию. Будем искать выход на консультации, когторая состоится на седьмом уроке.

LM : LN = 12 : 18 = 2 : 3

LN : KN = 18 : 27 = 2 : 3

ﮮ1 = ﮮ2, как накрест лежащие, образованные при пересечении параллельных LM и KN секущей LN.

Треугольники подобны по второму признаку подобия треугольников.

.

Через минуту.

Представитель одной группы, предлагает составленый их группой план, все слушают, корректируют.

В результате приходят к следующему ходу решения:

Прочитать предложенный чертёж, перевести задачу на математический язык.

Определить к какому виду относится задача.

Отобрать необходимый теоретический материал.

Выполнить необходимые вычисления.

Представители групп дают ответ и комментируют своё решение.

Группа 1

Преставитель группы читает задачу.

На рисунке мы видим два прямоугольных подобных треугольника, поэтому отношение сходственных линейных элементов этих треугольников равно коэффициенту подобия. В данной задаче он равен 3. Поэтому высота столба в три раза больше, чем рост человека, тоесть равен 5,4 м. На такой высоте висит фонарь.

Группа 2

Преставитель группы 2читает задачу.

Для решения можно воспользоваться установленным фактом.

Получается, что конец длинного плеча опустится в колодец преодалев расстояние в пять раз бльшее, чем расстояние, которое преодалеет короткий конец плеча, то есть 5м

Группа3.

Представитель читает задачу.

На рисунке есть два подобных треугольника, с проведеными высотами к сходственным сторонам, поэтому чтобы осветить экран полностью расстояние нужно увеличить в два раза.

Расстояние будет равно 480 см

Корректируют решение.

10мин

5

Рефлексия

Ребята, мы с вами хорошо потрудились, пришло время подвести итоги.

Давайте вспомним, чем мы занимались на уроке.

Где это может пригодиться?

А теперь каждый из вас получитоценочный лист, в котором перечислены виды деятельности, в которых каждый принимал участие.

Подумайте, что у вас получалось хорошо, не вызвало затруднений, что не удалось, где потребовалась помощь

Оцените свою работу по предложенным видам деятельности.

Подсчитайте плюсики.

Каждый плюс даёт 1балл. Подсчитайте количество баллов набранных вами на уроке.

У кого набрано 7 баллов, поставьте в оценочном листе отметку»5»,

у кого набрано 5, 6 баллов – отметку «4».

Поставьте эти отметки в дневник.

Остальным советую не отчаиваться, у вас всё впереди.

Отметки за урок самым активным представителям групп.

Систематизировали знания, сделали новое для себя открытие, убедились в том, что применяя его можно красиво решать задачи.

Поможет успешно справиться с экзаменом по математике.

Оценивает каждый свою работу по предложенным видам деятельности, выставляют рейтинговые баллы

5мин

6

Домашнее задание.

П. 14. 1 – 14. 4 , №24 стр.103(ОГЭ),

№19*(ПО ГРУППАМ)

Записывают в дневник, просматривают в учебнике

2мин