Подобие треугольников. Решение практических задач»

Тема урока «Подобие треугольников. Решение практических задач»

Тип урока:  урок общеметодологической направленности

Дидактическая задача: Формирование универсальный учебных действий (УУД) в условии решения практических задач

Цель урока:

деятельностная: совершенствование представлений о широком применении подобия треугольников в решении практических задач,

развитие способностей учащихся к новому способу действия, связанному с изученным понятием.

содержательная: совершенствование умений применять теоретические знания  при решении практических задач

План урока

1. Организационный момент, формулировка темы и целей урока.
2. Актуализация усвоенных УУД  знаний учащихся
3. Применение теоретических основ при решении практических задач.
4. Подведение итогов. Рефлексия.

Ход урока

    1. Организационный момент

У:     Здравствуйте ребята.

Начать наш урок я хочу со слов  А.Н. Крылова

«Рано или поздно всякая правильная математическая идея находит применение в том или ином деле».

    Как вы считаете нужна ли вам математика в обыденной жизни?

Отв: знания математики необходимы нам в жизни.

   У:     совершенно верно. Без математики в жизни нам не обойтись   и сегодня мы   попробуем применить известные вам учебные   действия при решении практических задач.

Посмотрите как вы сегодня сидите?

Отв: по группам

У: Я думаю, что работа в группах позволит создать нам комфортную обстановку для успешной работы на уроке.

     Алина, вы сегодня бесподобны!

Миша, как ты думаешь, что я имела в виду?

Отв:    уникальны, единственны в своём роде, оригинальны, отличаетесь от других.

У:   Сравним два понятия и выделим их свойства.

Бесподобное  

Непохожее

Несравнимое

Единственность

Оригинальность

 Подобное

Похожее

Можно сравнить

Множественность

аналогичность

Я думаю, вы догадались о чём пойдёт речь?

Отв: о подобии фигур, подобие треугольников.

У:    Запишем тему урока:  Подобие треугольников. Решение практических задач.

А какая будет цель?

Отв: научиться решать практические задачи.

У:    Да, совершенно верно, сегодня мы будем применять теоретические знания для решения практических задач.

2. Актуализация усвоенных учебных действий учащихся.

  У :     Сейчас вы получили индивидуальные карты, в которых будем работать во время урока, и сигнальные карточки двух цветов. С помощью них вы дадите мне ответ о том, истинно или ложно высказывание. Ответ да  - вы поднимаете зелёную карточку, ответ нет  - красную.

1. Два треугольника подобны, если их углы соответственно равны и сходственные стороны пропорциональны.       Да

1. Два равносторонних треугольника всегда подобны.             Да

1. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны?                             Да

1. Отношение периметров двух подобных треугольников равно квадрату коэффициента подобии.      Нет

1. Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.       Да

1. Любые два прямоугольных треугольника подобны.   Нет

У :  А когда можно утверждать, что прямоугольные треугольники подобны?

Отв: когда в прямоугольных треугольниках по одному равному острому углу. Первый признак

Отв: когда прямоугольный треугольник – равнобедренный. Второй признак

У:      Посмотрите в индивидуальные карты, там есть таблица. Каждый столбец имеет своё название: что я знаю? что я хочу узнать?  что я узнал?

 Заполните первый столбец, ответив себе на вопрос,  что я знаю по теме «Подобие треугольников»?

что я знаю?

что я хочу узнать ?

что я узнал?

определение подобия треугольников

признаки подобия треугольников

Учащиеся заполняют первый столбец.

З.   Применение теоретических основ при решении практических задач

 Отложили листочки и внимательно слушаем увлекательную легенду.

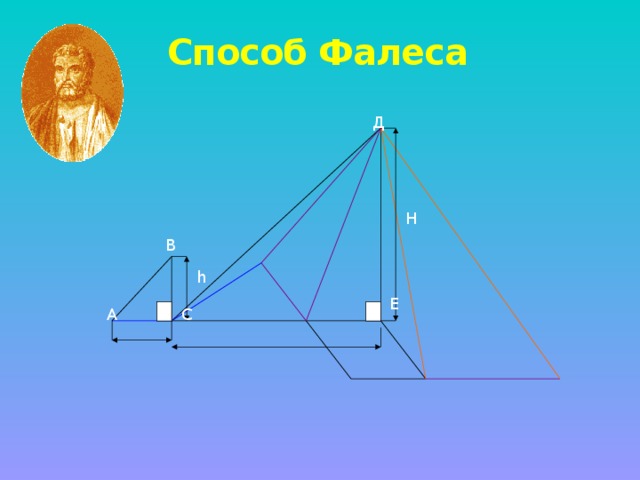
В один из солнечных дней Фалес вместе с главным жрецом храма Изиды прогуливался мимо пирамиды Хеопса.

 Знает ли кто-либо какова её высота? – спросил он.

Нет, сын мой, - ответил ему жрец,  древние папирусы не сохранили нам этого, а наши знания не дают о ней судить даже приблизительно.

 Но ведь определить высоту пирамида можно совсем точно и прямо сейчас. –воскликнул Фалес.

Вопрос вам -  какие математические знания он использовал для определения высоты пирамиды?

Отв: Может быть он применил подобие треугольников?

У : совершенно верно.

Вот смотрите, - продолжал Фалес, - мой рост составляет три царских вавилонских локтя. А вот моя тень. Её длина такая же. И какой бы мы предмет не взяли именно в это время тень от него, если поставить его вертикально, отбрасываемая тень точно равна высоте предмета.

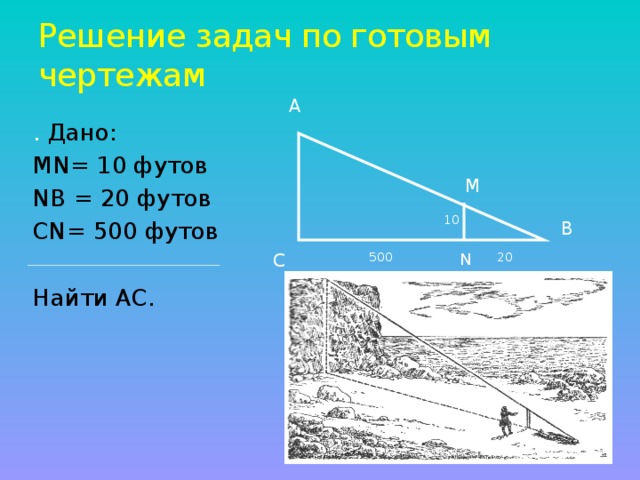
 Вот так выглядит модель решения этой задачи.( прокомментировать рисунок) (см презентацию  к уроку)

У     Скажите, в современном мире есть необходимость измерить высоту большого объекта? 

Отв:  Да

У :     Посмотрите на свои таблицы, как  вы считаете теперь сможете, заполнить второй столбец. Сделайте это.

( заполняют вторую часть таблицы)

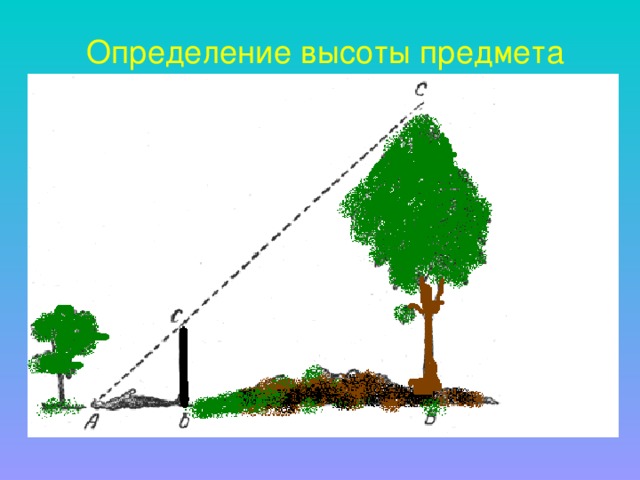
У           Вы были правы, когда сказали, что в современном мире есть необходимость измерить высоту больших объектов?  Этими объектами могут быть телеграфные столбы, башни, здания. Способы измерения высоты таких объектов весьма разнообразны. Я вам предлагаю решить эту задачу разными способами.

Сейчас у вас есть возможность проявить свои способности в групповой работе.

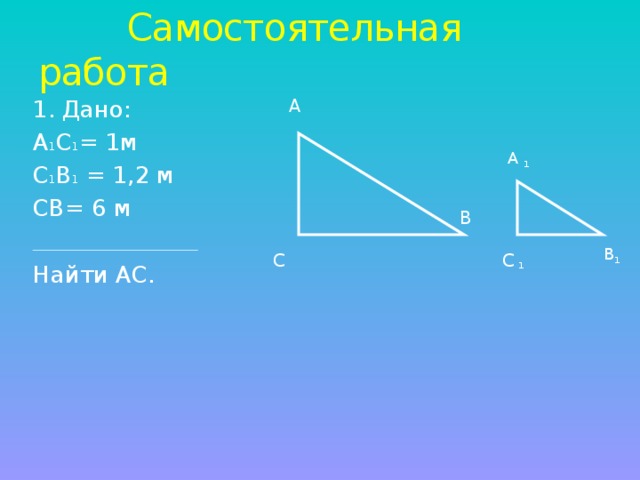
Я предлагаю решить задачу по готовому чертежу. Итак, каждая группа получает свою задачу, оформленную на листе. Используя данные, через несколько минут вы назовёте высоту дерева. Приступаем.( задачи из учебника № 581,580)

Обратите внимание, на столе у вас лежат учебники, откройте их и можете пользоваться.

   У: Ваше время истекло. Справились с работой? Я предлагаю поделиться    своим решением. Вынесите задачу на доску.

( кратко выслушать решение одной задачи задач)

Спасибо.

У:  сейчас вы решали задачу предложенную мной. Но в жизни часто приходится самостоятельно принимать решения, используя и те знания, которые  получили в школе. 

Посмотрите вокруг себя. Где вы можете применить знания подобия треугольников?

Отв:  измерить высоту кабинета.

У  Да, это задача будет нам по силам.  Но я не вижу здесь лестницы? Какими средствами мы можем это сделать?

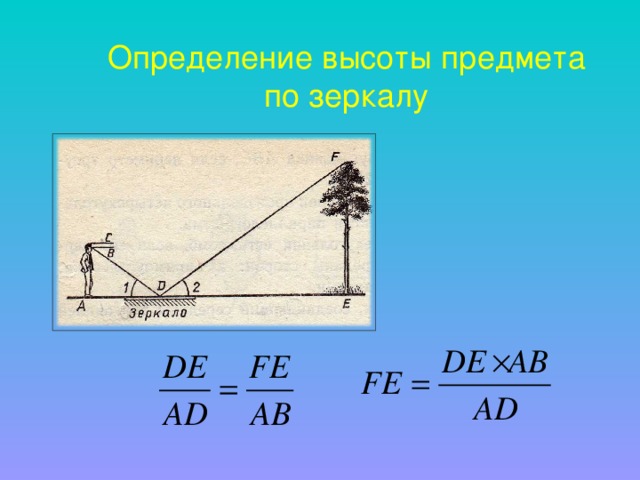
Отв: рулеткой и зеркалом.

У : интересное предложение. Давайте попробуем. Итак, мы формулируем задачу…(выходят к доске 3 человека)

Отв: измерить высоту кабинета.

У.        Давайте определимся, что мы будем считать высотой кабинета?

Отв:     Расстояние от плинтуса до потолка.

У        Т.Е.расстояние между двумя параллельными прямыми. Итак, у нас есть рулетка, зеркало и калькулятор. Как мы их должны использовать?

Без математической модели здесь не обойтись.

Выполним рисунок на доске и в тетради, произведем необходимые измерения и определим неизвестную величину.

1. Подведение итогов. Рефлексия.

У: Начиная урок, мы поставили цель научиться применять теоретические знания в решении практических задач.

 Достигли мы её?

Отв: да

Удачна ли была ваша совместная работа?

Отв:  да

    Предлагаю вернуться к таблицам и заполнить её до конца. Поставьте сами себе оценку за урок на этом листе.

Закончили работу. Молодцы. Сдайте  индивидуальные карты. И запишем домашнее задание: дома измерьте высоту своей комнаты, П 64, стр 149.

На память о нашем уроке, я хочу раздать вам буклеты. В них вы найдёте больше информации о подобии фигур. И кто знает, может быть, с кем-то из вас я встречусь на научно-практической конференции, где вы будете рассказывать о бесподобном подобии.

 Спасибо за урок.