| Тема урока: Применение производной при решении практических задач | КГУ «Гимназия № 15»
|
| Дата: 13.04.2017 года | Ткаченко Т.Д. |
| Класс: 10Б Количество присутствующих: 18 | Количество отсутствующих: 2 |
| Цели: | Развитие умений самостоятельно применять знания, умения и навыки и осуществлять их перенос в новые условия. |
| Цели обучения: | |
Развитие умения сравнивать, анализировать, сопоставлять, делать выводы. Развитие умений самостоятельно работать, умения ясно выражать свои мысли, умений проводить самооценку учебной деятельности на уроке. Развитие умений участвовать в дискуссии, умение слушать и слышать. Развитие познавательного интереса к предмету |
воспитание коммуникативной и информационной культуры обучающихся; эстетическое воспитание осуществляется через формирование умения рационально, аккуратно оформлять задание на доске и в тетради.
|
| Ожидаемые результаты: | |
| |
|
|
| Предыдущее обучение: | Знают правила дифференцирования и таблицу производных Знают алгоритмы нахождения промежутков возрастания и убывания функции, критических точек функции и наибольшего и наименьшего значения функции; |
|
| |
|
| |
| Планируемые сроки | Время | Планируемые действия |
| Начало урока: | |
|
| 1.Организационный этап
| 2 мин
| Подготовка к уроку. Приветствие. Формирование групп по номерам 1, 2, 3,4. Распределение ролей в группах. Тема записана на доске |
| 2. Фаза вызова
а) | 2мин
3 мин | Работа в группах: определение целей и задач урока. Каждая группа высказывает свое мнение.
Найти ошибку. Проверка теоретического материала. Отвечать должны только да или нет. + – верно, _ – неверно, есть ошибка. Работа индивидуальная.
1. Функция возрастает на [-7; 2) и (2; 8], значит, она возрастает на [-7; 8]. Верно ли?
2. Производная функции в точке а равна 0, значит а - критическая точка. Верно ли?
3. Производная функции не существует в точке а, значит а - критическая точка. Верно ли?
4. Критическая точка является точкой экстремума. Верно ли?
5. Точка экстремума является критической точкой. Верно ли?
Проверка; нет, да; да; нет; да Проверка, 5 правильных ответов оценка «5», 4-«4», 3-«3», 2-0 оценка «2». Взаимопроверка.
|
|
| 3 мин | Мозговой штурм «Где применяют производную для решения задач в различных областей науки?». - Применение физического смысла производной при решении физических задач - Решение химических и биологических задач с помощью производной - Решение задач с географическим содержанием – - Решение математических задач с помощью производной Взаимооценка (группы параллельно оценивают друг друга, используя сигнальные карточки). |
| Середина урока | 2 мин | Деловая игра. Учащимся предстоит подтвердить универсальность открытия английским ученым Исааком Ньютоном дифференциального исчисления. Для работы организованы четыре группы: математиков, физиков, экономистов и историков. Каждая группа специалистов получает задание. Прием «Анализ текста по предложенной схеме». Учащиеся получают распечатанный текст задания. Задания доступны для понимания школьниками. Ученикам нужно провести анализ данного задания, составить вопросы , зафиксированные на доске (ромашка Блума) и подтвердить универсальность открытия. В конце работы происходит обсуждение различных вариантов ответов и разбираются затруднения, возникшие в ходе выполнения задания. |
| 3. Фаза реализации смысла
| 5 мин | 1. Задание историкам ( философам)
В 490-430 гг. до н. э. древнегреческий философ Зенон Элейский привел логические доказательства невозможности движения, выраженные в знаменитых парадоксах – апориях (по-гречески «а» означает отрицание «порос» - выход, слово же «апория» переводится как «затруднение», «безвыходное положение»). Так в апории «Дихотомия» говорится: «Чтобы преодолеть некоторое расстояние АВ, человек должен сначала пройти половину этого расстояния АС. А чтобы пройти половину расстояния АС, ему нужно пройти половину половины АД - и так до бесконечности. В итоге мы придем к выводу, что человек вообще не в состоянии сдвинутся с места, так как всегда можно поставить перед ним условия пройти половину сколь угодно малого пути». Пользуясь понятием мгновенной скорости, поясните, в чем состоят заблуждения Зенона. Ньютон определил производную как скорость механического движения. Но движение — одно из основополагающих понятий философии. Философский аспект открытия производной — направление вашего исследования.
|
|
| 5 мин | 2. Задание математикам.
1) Подготовьте краткое выступление о сути открытия производной. 2) Объясните следующее высказывание Ньютона: «Когда величина является максимальной или минимальной, в этот момент она не течет ни вперед, ни назад». 3) Ответьте на вопрос: какие задачи называются задачами на оптимизацию или экстремальными? 4) Решите задачи. А. Командиру межгалактического космического корабля, движущемуся по закону Х(t) = 1 + 6t + 3t2- t3 сообщили о том, что приборы зафиксировали неопознанный летающий объект, стремительно приближающийся к кораблю. Чтобы избежать столкновения, необходимо максимально увеличить скорость. Каким должно быть ускорение корабля в момент, когда скорость станет максимальной? Б. Сопротивление f (V) дороги движению автомобиля при скорости движения автомобиля Vкм/ч выражается следующими формулами: а) На асфальте:f(V) =14,5 + О,25V. б) На шоссейной дороге: f(V) = 24— 2/3V+ 1/16V2. в) На мягкой грунтовой дороге: f(V)= 36,5— 3/4V+ 1/3ОV2. Определите скорость, при которой сопротивление будет наименьшим. |
| | 5 мин | Задание физикам.
Открытие Ньютоном производной стало переворотным пунктом в истории естествознания. Оказалось, что связь между количественными характеристиками самых различных неравномерно протекающих процессов, исследуемых физикой, химией, биологией аналогична связи между путем и скоростью. Покажите, как различные физические понятия получают единую трактовку c точки зрения производной. Для получения ответа на главный вопрос, можете выполнить следующие заданиями. 1) При равномерном движении тела по окружности угловой скоростью тела называется угол поворота в единицу времени. Дайте определение угловой скорости для неравномерного движения. (Запишите формулу, используя производную.) 2) При равномерном протекании заряда по проводнику силой тока называется заряд, протекающий за единицу времени. Сформулируйте определение силы тока при неравномерном протекании заряда. (Запишите формулу, используя производную.) 3) Используя понятие производной, сформулируйте определение: а) линейной плотности неоднородного стержня; б) теплоемкости; в) давления; г) ускорения при прямолинейном неравномерном движении; д) мощности. При подготовке к ответу можете использовать справочник по физике: О. Ф. Кабардина и энциклопедический словарь юного физика. 4) Решите задачи: 1. Сила тока I изменяется в зависимости от времени t по закону I = 2t— 5t (I— в амперах, t — в секундах.) Найти скорость изменения силы тока в конце 10-й секунды. 2. Тело массой 10 кг движется прямолинейно по закону S= 3t2 + t +4. Найти кинетическую энергию тела чрез 4 сек. после начала движения. 3.Тело массой 2 кг движется прямолинейно по закону: х(t) = t3— 3t2 +2, где х(t) измеряется в метрах, время t— в сек. Найти силу, действующую на тело в момент времени t = З сек. 4. Закон движения частицы: х(t) = t3 — 3t, где х(t) измеряется в метрах, время t в секундах. Каково ускорение частицы в момент времени, когда скорость ее равна 11 м/с?
|
|
| 5 мин | 4. Задание экономистам. 1. Классическая экономика оперирует средними величинами: средняя цена, средняя производительность труда и т. д. Но постепенно сложился иной подход. Существенные закономерности нужно искать в области не средних, а предельных величин. Предельные или пограничные величины характеризуют не состояние (как суммарная или средняя величины), а процесс, изменение экономического объекта. Следовательно, производная выступает как скорость изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора. Приведите примеры предельных величин в экономике. 2. Производная — скорость изменения функции. Задав различные экономические процессы функционально, исследуя полученные функции с помощью производной, можно с большей достоверностью делать экономические прогнозы. Приведите примеры экономических функций. 3. Решите задачи. 1) Цементный завод производит Х тонн цемента в день. По договору он должен ежедневно поставлять строительной фирме не менее 20 т цемента. Производственные мощности завода таковы, что выпуск цемента не может превышать 90т в день. Определить, при каком объеме производства удельные затраты будут наибольшими, если функция затрат имеет вид k(х) = -х3 + 98х2 + 200х. (Удельные затраты — это затраты на единицу продукции.) 2) Пиццерия «Сицилия» специализируется на приготовлении особого вида пиццы и славится изысканным обслуживанием посетителей, что позволило ей полностью монополизировать рынок производства данного вида пиццы на острове Сицилия. Ее общие издержки (С) за один день работы зависят от количества выпускаемой пиццы (Q) следующим образом: С(Q) = Q2+ 500. Зависимость дневной выручки пиццерии (R) от количества проданных пицц задается так: R(Q)= 400Q—Q2 Сколько пицц в день нужно выпекать поварам из «Сицилии», чтобы пиццерия получала за день максимально возможную прибыль? Чему равна величина этой прибыли? 3) Затраты на перевозку груза пароходом между двумя портами складываются из двух частей: одна часть прямо пропорциональна времени, затраченному на перевозку (с коэффициентом а), вторая скорости движения (с коэффициентом в). Найти оптимальную по затратам скорость перевозки груза, если расстояние между портами равно 900 км, а: Ь = 1 : 4, время измеряется в часах, а расстояние в километрах. |
|
| 7 мин | После выполнения заданий либо руководители групп, либо сами «эксперты» отчитываются перед ученым советом, состоящим из трех-четырех учащихся, принимавших активное участие в подготовке заданий (они могут быть делегированы группами как лучшие эксперты в своей области). .“Ромашка” Блума. По теме составить вопросы, учитывая их назначение.
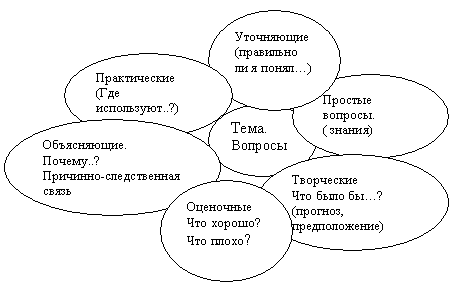
|
| Конец урока | 1 мин | Целью нашего сегодняшнего урока было научиться анализировать реальные ситуации с помощью доступного нам математического аппарата. Мы рассмотрели, как методами математики, а если точнее, то мат. анализа, а если точнее, то его разделом «Дифференциальное исчисление», можно решать экономические задачи, т.е. задачи, на первый взгляд, далёкие от математики. Очень часто, решая задачу на математики, особенно, если она даётся нам не легко, мы думаем: « А зачем нам всё это надо?» - А вот затем и надо, чтобы суметь применить полученные знания для решения, на первый взгляд, совсем нематематической задачи, я уж не говорю о таких науках, как физика и химия. Ведь недаром Лейбниц сказал, что если наши открытия не подтверждены математически, то и нет никакой уверенности в их достоверности.
|
| Дополнитель ная информация | 1 мин | Подводя итоги приведенных рассуждений, можно утверждать, что дифференциальное исчисление и его основные принципы – это граница между античной наукой и наукой нового времени. Ведь именно в рамках развития данного метода была совершена переоценка взглядов на математику, преобразившая не только отдельно взятую научную дисциплину, но и методологию науки в целом. Одной из самых значимых особенностей истории развития дифференциального исчисления как важнейшего научного метода было его изначальное возникновение как прикладного метода у многих известных ученых XVI-XVII вв., большинство из которых тем или иным образом продолжали идеи Николая Кузанского, изложенные еще в XV веке. Такое начало позволило сформировать огромный пласт знаний и суждений, что привело к оформлению дифференциального исчисления как полноценного, а впоследствии и важнейшего, научного математического метода познания мира.
|
| Фаза рефлексии:
| 3 мин | Как вы считаете, кто из вас работал в полную силу своих возможностей, чувствовал себя уверенно?
А кто из вас работал хорошо, но не полную силу, испытывал чувство неуверенности, боязни, что отвечу неправильно?
А у кого из вас не было желания работать, то есть сегодня не ваш день? Я хочу вам пожелать, чтобы у вас была только положительная производная, чтобы знания ваши только возрастали. Спасибо за урок!
|
| Итог урока, домашнее задание | 2 мин | Дома. Повторить формулы и алгоритмы. Задача № 1. Пусть функция затрат при производстве апатитового концентрата имеет вид: К(Х)=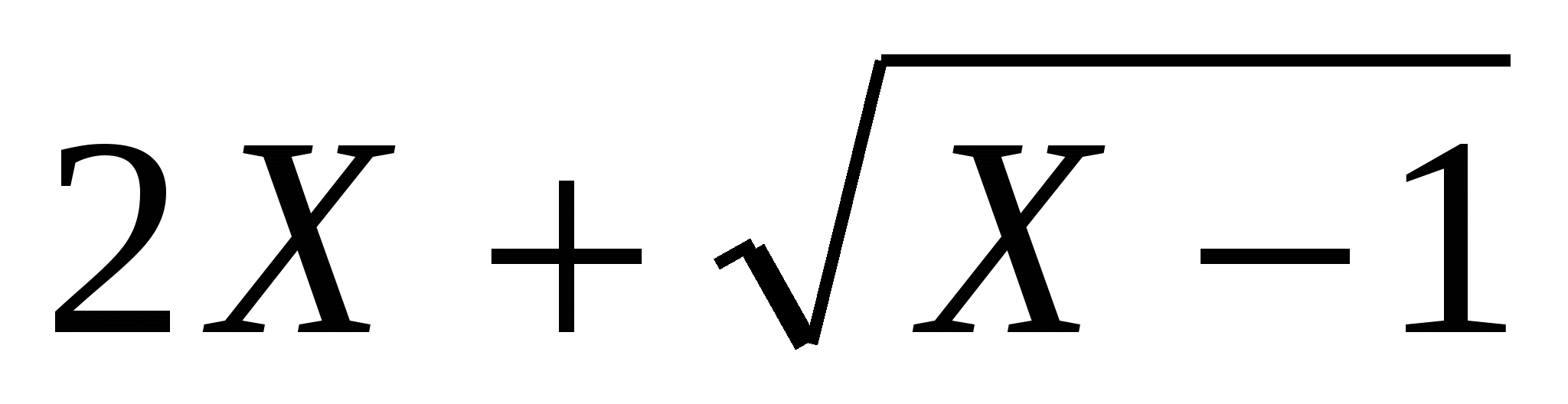 . Определить предельные издержки производства при увеличении объёма выпуска на . Определить предельные издержки производства при увеличении объёма выпуска на 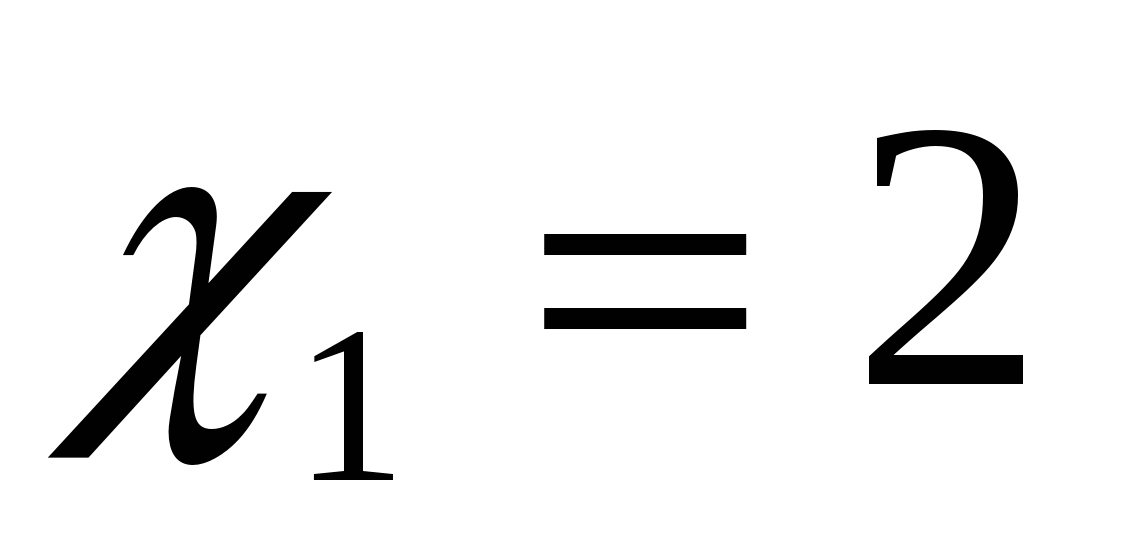 ед. и на ед. и на 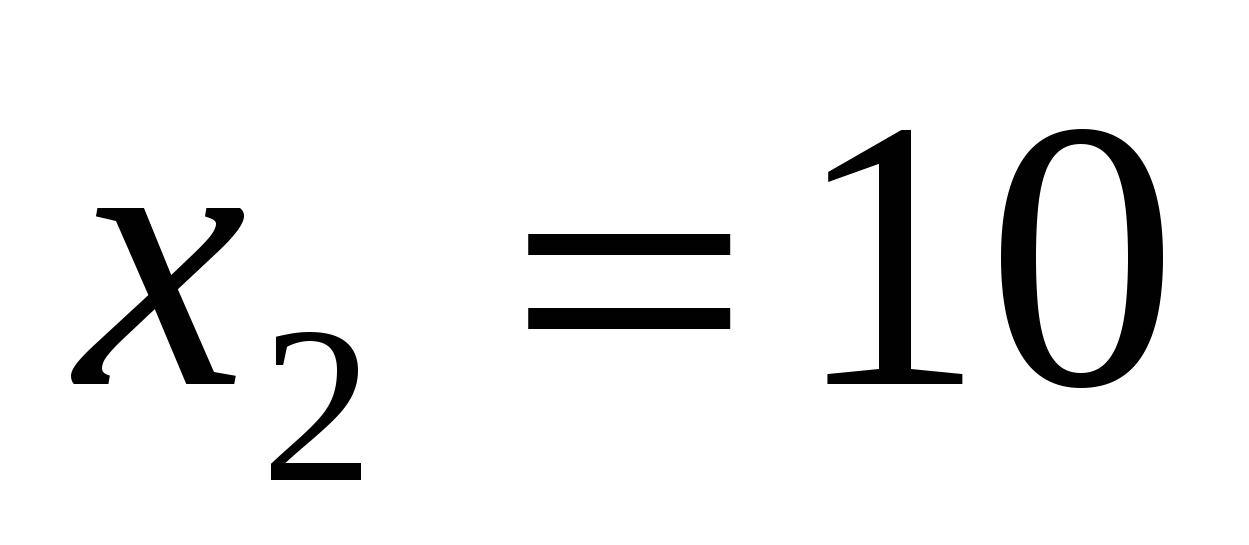 ед. ед. Задача № 2. Предприятие производит Х единиц продукции. Установлено, что зависимость финансовых накоплений от объёма выпуска задаётся формулой: 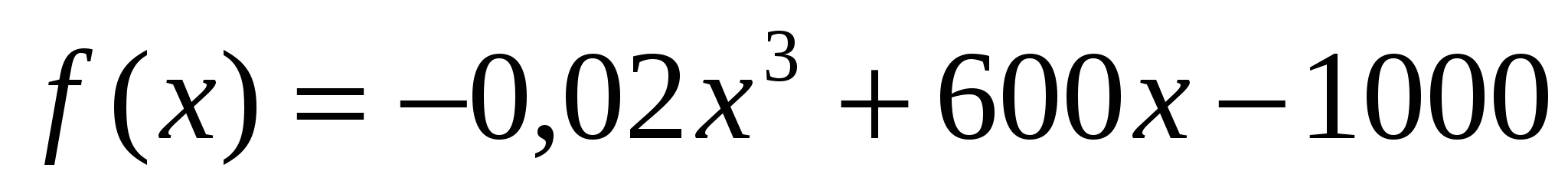 . . Определить максимально возможную величину финансовых накоплений. Вопрос: переведите экономический вопрос задачи на математический язык, или др. словами составьте математическую модель данной задачи. Задача № 3. Цементный завод производит X тонн цемента в день. По договору н должен ежедневно поставлять строительной фирме не менее 20 тонн цемента. Производственные мощности завода таковы, что выпуск не может превышать 90 тонн в день. Определить: 1) при каком объёме производства удельные затраты производства будут наибольшими ( наименьшими); 2) выгодно ли строительной фирме быть единственным партнёром завода. Функция суммарных затрат имеет вид: 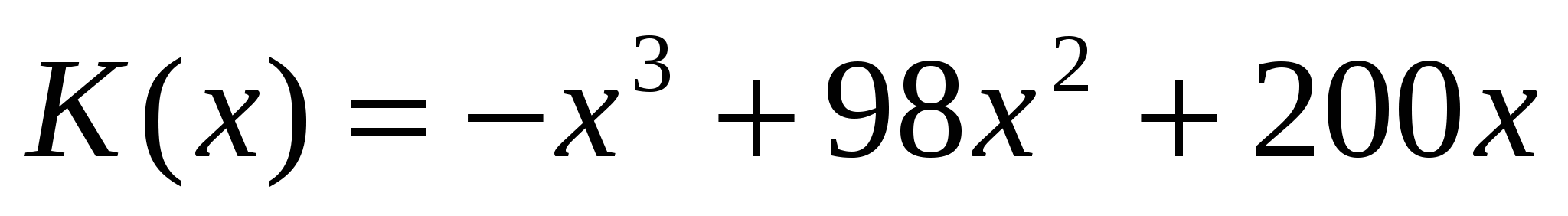 . .
|
О - Отлично изучил тему.
a - Есть пробелы, но я их решил самостоятельно.
N - Были пробелы, но я их решил с помощью группы.
// - Проблемы не решены.
Учитель ставит итоговую отметку, оценив деятельность всей группы.

















