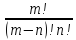Практическая работа: «Комбинаторика»

Работа для проверки знаний по теме "Комбинаторика".

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Практическая работа: «Комбинаторика»»

Практическая работа: «Комбинаторика»

Вариант 1

Вариант 2

Перестановки P_n= n!

Сколькими способами можно рассадить пятерых детей на пяти стульях в столовой детского сада?
Сколькими способами можно установить дежурство по одному человеку в день среди 6 (5, 7) учащихся класса в течение 6 (5, 7) дней?
Сколько различных семизначных чисел, не содержащих одинаковых цифр, можно записать с помощью цифр 0, 1, 2, 3, 4, 5, 6 так чтобы: 1) последней была цифра 0, 2) первой была цифра 4, 3) первой цифра 3, а последней цифра 5?

1. Перестановки P_n= n!

1. Сколькими способами можно рассадить пятерых детей на пяти стульях в столовой детского сада?

2. Сколькими способами можно установить дежурство по одному человеку в день среди 4 (8, 9) учащихся класса в течение 4 (8, 9) дней?

3. Сколько различных восьмизначных чисел, не содержащих одинаковых цифр, можно записать с помощью цифр 0, 1, 2, 3, 4, 5, 6, 7 так чтобы: 1) последней была цифра 0, 2) первой была цифра 4, 3) первой цифра 3, а последней цифра 5?

Размещения A ⁿ_m= m(m-1)(m-2)*…*(m-(n-1))

Сколько существует способов для обозначения с помощью букв A, B, C, D, E, F, G вершин данного: 1) треугольника, 2) пятиугольника?
В классе 25 учеников. Сколькими способами из их числа можно сделать назначение: 1) физорга и культорга, 2) физорга, культорга и казначея?
В шахматном турнире участвуют: 1) 6 юношей и 2 девушки, 2) 5 юношей и 3 девушки. Сколькими способами могут распределиться места среди участников, если все наберут разное количество очков?

Размещения A ⁿ_m= m(m-1)(m-2)*…*(m-(n-1))

Сколько существует способов для обозначения с помощью букв A, B, C, D, E, F, G вершин данного: 1) четырехугольника, 2) шестиугольника?
В классе 27 учеников. Сколькими способами из их числа можно сделать назначение: 1) физорга и культорга, 2) физорга, культорга и казначея?

3. В шахматном турнире участвуют: 1) 7 юношей и 2 девушки, 2)5 юношей и 4 девушки. Сколькими способами могут распределиться места среди участников, если все наберут разное количество очков?

3. Сочетания С ⁿ_m=

1. Сколькими способами для участия в соревнованиях из 9 человек можно выбрать: 1) 4 студентов, 2) 5 студентов?

2. На плоскости отмечено: 1) 16 точек, 2) 13 точек, причем никакие 3 из низ не лежат на одной прямой. Сколько различных отрезков можно построить, соединяя эти точки попарно?

3. На окружности отмечено: 1) 7 точек, 2) 8 точек. Сколько различных треугольников с вершинами, выбранными из этих точек, можно построить?

3. Сочетания С ⁿ_m=

1. Сколькими способами для участия в соревнованиях из 11 человек можно выбрать: 1) 6 студентов, 2) 7 студентов?

2. На плоскости отмечено: 1) 15 точек, 2) 14 точек, причем никакие 3 из низ не лежат на одной прямой. Сколько различных отрезков можно построить, соединяя эти точки попарно?

3. На окружности отмечено: 1) 5 точек, 2) 10 точек. Сколько различных треугольников с вершинами, выбранными из этих точек, можно построить?

Оценка: «3» - 6 заданий

«4» - 7 заданий

«5» - от 8 заданий

Оценка: «3» - 6 заданий

«4» - 7 заданий

«5» - от 8 заданий

Дополнительное задание:

Записать разложение бинома (3x + 4)⁴

Дополнительное задание:

Записать разложение бинома (2x + 3)⁴

Предмет: Математика

Категория: Уроки

Целевая аудитория: Прочее

Скачать
Практическая работа: «Комбинаторика»

Автор: Бухарина Юлия Юрьевна

Дата: 10.09.2017

Номер свидетельства: 427754

Похожие файлы

Практическая работа по теме «Комбинаторика»

object(ArrayObject)#851 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(82) "Практическая работа по теме «Комбинаторика»"
    ["seo_title"] => string(43) "prakticheskaia_rabota_po_teme_kombinatorika"
    ["file_id"] => string(6) "513806"
    ["category_seo"] => string(7) "algebra"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1559898257"
  }
}

Элементы комбинаторики. Решение задач на вычисление числа размещений, перестановок и сочетаний.

object(ArrayObject)#873 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(177) "Элементы комбинаторики. Решение задач на вычисление числа размещений, перестановок и сочетаний."
    ["seo_title"] => string(80) "eliemienty_kombinatoriki_rieshieniie_zadach_na_vychislieniie_chisla_razmieshchie"
    ["file_id"] => string(6) "380626"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(7) "prochee"
    ["date"] => string(10) "1484677514"
  }
}

Презентация " Создание комплектов школьной формы с помощью методов комбинаторики"

object(ArrayObject)#851 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(151) "Презентация " Создание комплектов школьной формы с помощью методов комбинаторики""
    ["seo_title"] => string(80) "priezientatsiia_sozdaniie_kompliektov_shkol_noi_formy_s_pomoshch_iu_mietodov_kom"
    ["file_id"] => string(6) "385078"
    ["category_seo"] => string(10) "vneurochka"
    ["subcategory_seo"] => string(11) "presentacii"
    ["date"] => string(10) "1485681889"
  }
}

Проектная деятельность по теме "Комбинаторика"

object(ArrayObject)#873 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(87) "Проектная деятельность по теме "Комбинаторика" "
    ["seo_title"] => string(50) "proiektnaia-dieiatiel-nost-po-tiemie-kombinatorika"
    ["file_id"] => string(6) "223426"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1437662410"
  }
}

Электив для 9-х классов "Начальные сведения из теории вероятностей"

object(ArrayObject)#851 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(123) "Электив для 9-х классов "Начальные сведения из теории вероятностей" "
    ["seo_title"] => string(77) "eliektiv-dlia-9-kh-klassov-nachal-nyie-sviedieniia-iz-tieorii-vieroiatnostiei"
    ["file_id"] => string(6) "119792"
    ["category_seo"] => string(11) "informatika"
    ["subcategory_seo"] => string(12) "planirovanie"
    ["date"] => string(10) "1413526448"
  }
}

Практическая работа: «Комбинаторика»

Просмотр содержимого документа «Практическая работа: «Комбинаторика»»

Похожие файлы

Полезное для учителя

Просмотр содержимого документа
«Практическая работа: «Комбинаторика»»