Введение. Ученик должен обладать хорошей геометрической базой, которая должна помочь ему в дальнейшей жизни и в выборе профессии. Геометрию невозможно понимать без знания её исторического развития, и вклада выдающихся ученых-геометров в создании геометрии как науки. Ведь известные геометрические теоремы, утверждения и свойства фигур возникли из практических потребностей человека. История геометрии носит эволюционный характер, поэтому начинающему 8-ми класснику очень важно знать причину возникновения известных теорем и способы их доказательства, т.к. практическое применение связано с теоретическими знаниями, мы связали эти два основных блока в теории и в практике. Учитывая, что данная тема имеет свое место в математике и важна в практической жизни, определена цель работы: рассмотреть историческую роль Фалеса в геометрии и применить подобие треугольников в практической жизни людей.
Для достижения цели определены задачи: Познакомиться с биографией Фалеса и значением его теорем.
- Рассмотреть применения подобия на практике и практических задачах.
- Изготовить «булавочный прибор».
- Создать рекламный буклет.
- Провести опрос по теме: «Значение Фалеса в мировой истории»
- Развивать познавательный интерес методами геометрии.
Таким образом мы позволяем учащимся расширить интеллектуальный кругозор в области геометрии с помощью изучения биографии выдающегося ученого Фалеса Милетского. Проект позволяет сделать сравнительную характеристику теорем доказанных в древности и в современной геометрии, изучить различные способы доказательств различных теорем. С помощью проекта ученики могут применить теоретические знания в практических задачах: Нахождение высоты памятника Определение ширины реки
В начале нашего исследования мы пользовались учебником по геометриие 7-9 классов (Атанасян Л.С.).
- Интернет ресурсами
- Материал и методика исследования
Данное исследование, как системная работа, было начато в январе 2012
года Меньщиковым Евгением ,Патраковым Виталием и Томшиным Артемом учащимися 8 «А» класса МБОУ СОШ №4 городского округа Стрежевой под руководством учителя математики Абдуллиной Ларисой Ивановной. Побудительным мотивом для начала исследования послужил недостаточный материал по данной теме в учебнике геометрии школьного курса, а так же широкое применение темы «Подобие треугольников» в практической жизни человека.
Архивный метод.
Во время работы над исследованием было изучено большое количество литературы по интересующей нас теме. Мы рассмотрели более десяти научных источников по большей части в области геометрических теорем, справочной литературы, а также интернет ресурсов, для этого мы прибегли к архивному методу (анализу документов, литературных источников), мы учитывали мнение ученого Фалеса Милетского, который, как оказалось, оказал большой вклад в изучении нашей темы. Более подробно литературный обзор приведен в одноименном разделе.
Опрос.
Метод опроса является одним из самых объективных и результативных методов сбора информации. Мы осуществляли опрос в виде,созданного нами опросника, с помощью теста, в котором были указаны несколько вариантов ответов, один из которых правильный. Опрос был направлен на получение необходимой информации, связанной с тематикой данной работы. Опрос мы проводили среди несколких возрастных групп: ученики, родители и учителя.
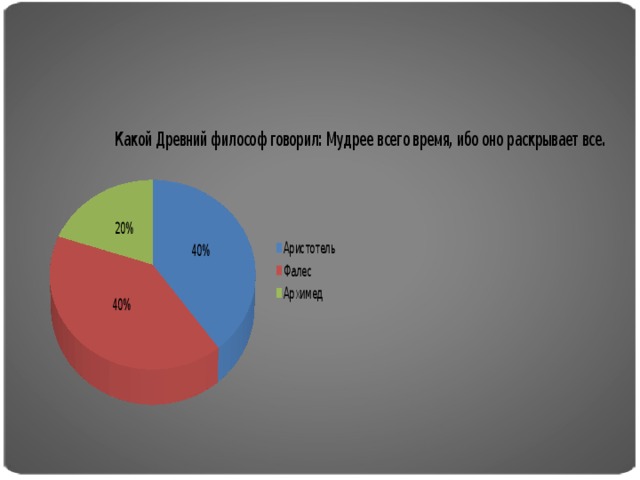
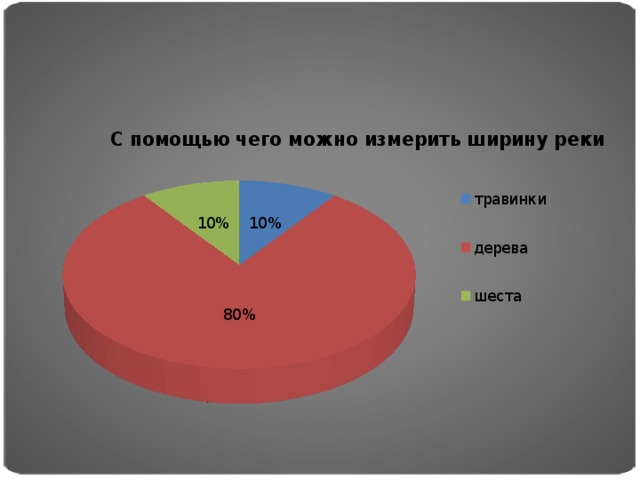
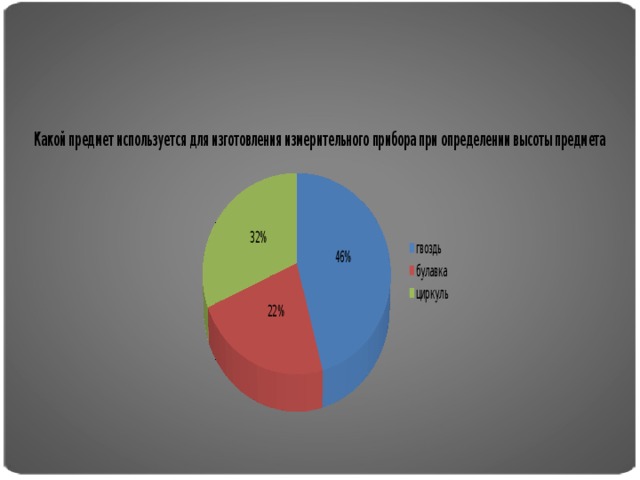
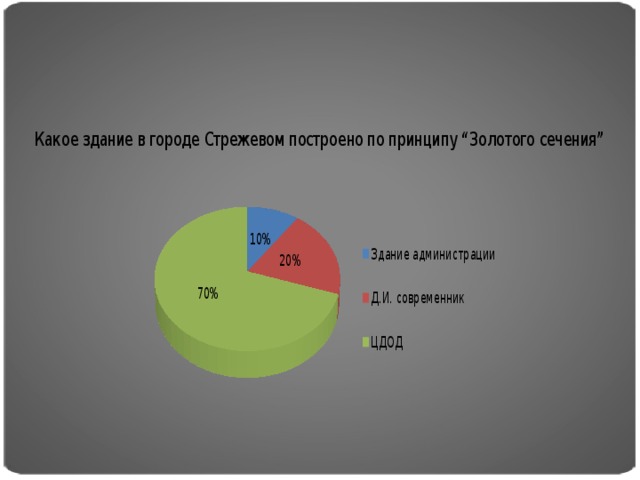
Цель опроса была следующей: узнать интеллектуальный уровень различных возрастных групп населения, в вопросах геометрии и применение ее на практике. Некоторые участники опроса, при ответах на вопросы пользовались интернет ресурсами. Нами было опрошено 50 человек, результаты опроса приведены в диаграммах.
Прикладной метод
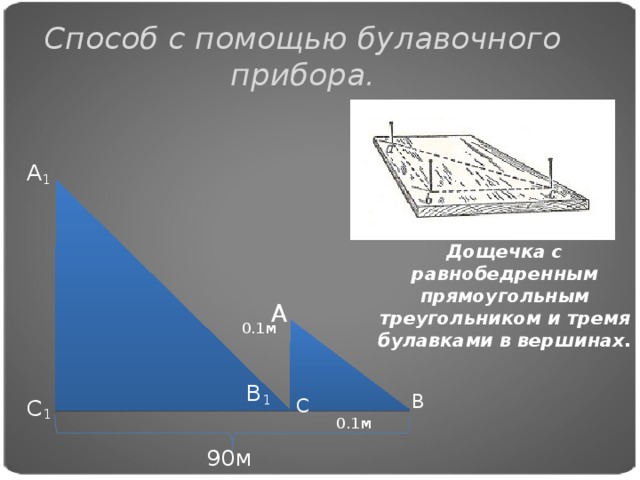
В проекте использован метод практических исследований, который позволяет использовать теоретические знания на практике. Изучив способы измерения высоты предмета с помощью различных простейших приборов, а именно с помощью шеста, тени, записной книжки, зеркала и булавочного прибора, мы в своем проекте выбрали булавочный прибор. Его изготовил Томшин Артем на уроках труда. Прибор мы использовали для измерения высоты памятника «Веник».Для нахождения ширины реки так же были изучены различные способы, но мы остановились на самом простейшем и удобном способе, который позволяет определять ширину реки в любых условиях.Достаточно иметь измерительную рулетку для определения расстояния. Прикладной метод полезен еще тем, что показывает геометрию, как прикладную науку, которую использует человек в своей жизнедеятельности.
4. «Теоретический и дидактический материал»
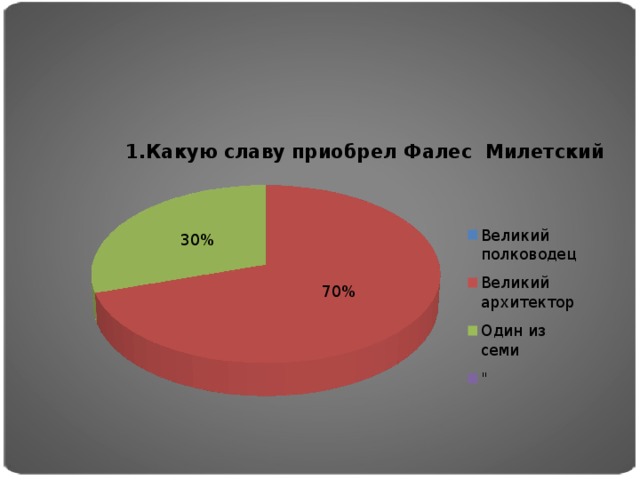
4.1. Использование основных теорем геометрии невозможно было без изучения биографии древнего и к сожалению не очень известного в современной геометрии ученого Фалеса Милетского. При изучении его биографии мы убедились в его исторической значимости .Фалес Милетский своими трудами , ученостью и мудростью создал себе славу: «Один из семи мудрецов древности» При изучении его биографии мы увидели своего рода
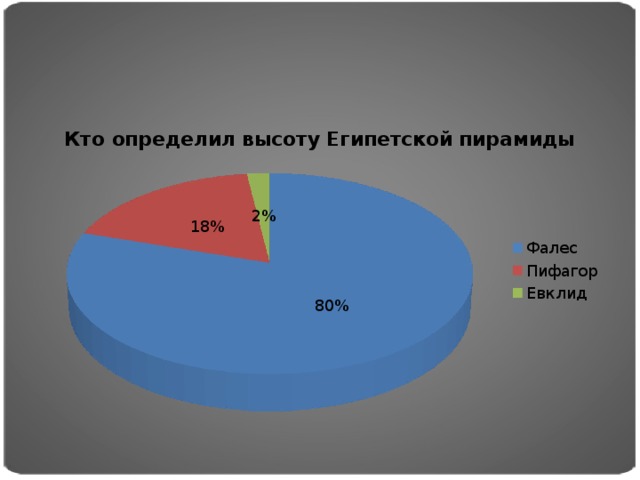
« историческую несправедливость», настолько известный ученый древности оказался незамеченным в современной истории, даже годы его проживания не известны окончательно. Мы изучили легенды о Фалесе и его теоремы. Кто же такой этот Фалес Милетский? Человек, который обрел славу одного из «семи мудрецов» древности. Фалес Милетский – древнегреческий философ, который отличился успехами в области астрономии, а также математики и физики. Годы его жизни были установлены только приблизительно: 625-645 гг до н.э. Одна из легенд о Фалесе состоит о нахождении высоты египетской пирмиды. Чтобы удивить фараона и остаться у него в фаворитах, Фалесу нужно было измерить высоту этой пирамиды. Фалес Милетский: использовал теорему подобия треугольников. Фалес подождал, пока длина его тени и его рост совпадут, а затем с помощью теоремы о подобии треугольников нашел длину тени пирамиды, которая, соответственно, была равна тени, отбрасываемой пирамидой.Фалес был не только ученым геометром, но так же астрономом и философом. Среди доказательств знания Фалесом астрономии можно привести следующий пример. 28 мая 585 г до н.э. предсказание Милетским солнечного затмения помогло прекратить длившуюся уже 6 лет войну между Лидией и Мидией. Это явление настолько испугало мидян, что они согласились на невыгодные для себя условия заключения мира с лидийцами.Фалес научился определять расстояние от берега до корабля, для чего использовал подобие треугольников. В основе этого способа лежит теорема, названная впоследствии теоремой Фалеса. Далеко от берега стоял на якоре корабль. Фалес сумел измерить расстояние от берега до корабля. В точности, как он это сделал, мы не знаем: его труды до нас не дошли.Значение Фалеса в истории геометрии настолько значимо, что его сравнивают с русским ученым М.В. Ломоносов. На гробнице Фалеса напечатаны следующие слова: Эта гробница мала, но слава над ней необъятна. В ней перед тобою сокрыт многоразумный Фалес.
Вторым этапом нашей работы применение подобия треугольников практическим задачам. Мы выбрали 2 основные задачи: определение высоты памятника «Веник» в городе Стрежевом и нахождение ширины реки в районе парковой зоны. Для осуществления первой задачи нами был изготовлен булавочный прибор с помощью которого мы определили высоту памятника.
При решении второй задачи определения ширины реки в помощью травинки мы использовали так же подобие треугольников. Описание способа: Сорвать травинку. Выбрать на противоположном берегу два куста.
Встать к ним лицом. Руки с травинкой вытянуть вперед и с ее помощью ее отмерить расстояние между кустами.
Глядеть на них одним глазом, сложить травинку вдвое и отходя от берега реки измерить расстояние до того момента когда травинка не закроет расстояние между кустами. Расстояние у нас получилось 12,5 м.
риложение
Для выявления актуальности темы мы создали опросник, и результаты опроса оформили в виде диаграмм.
Результат нашего проекта - создание рекламного буклета для значимости и актуальности темы «Фалес и подобие треугольников».
Выводы
Мы изучили литературные и интернет источники по теме: «Значимость Фалеса в истории геометрии, а так же применение подобия к задачам на практике» и пришли к следующим выводам:
Тема подобия одна из широкоприменяемых тем в жизни человека. В современном учебнике геометрии она полностью не раскрыта. Открытия древнего ученого Фалеса Милетского практически не упоминаются в учебнике. Основная его теорема о разбиении отрезка на равные части в учебнике геометрии используется как задача, а не теорема. В учебнике геометрии ничего не сказано о других важнейших теоремах, доказанных Фалесом, но способы измерения высоты предметов очень широко используется в жизни. Мы считаем, что изучение достижений Фалеса позволит ученикам глубже вникнуть в тему и понять ее значимость. Практические задачи которые рассматриваются в проекте не используются на уроках геометрии. Ученикам не известен способ измерения с помощью булавочного прибора и способ измерения с помощью травинки. Хотя данные способы можно применить в походных условиях. Результаты нашего опроса показали насколько низкий уровень интеллектуального развития населения в вопросах геометрии. В основном только 10% опрошенных людей ответили верно на заданные вопросы. Для этого мы создали рекламный буклет с целью повышения исторических и теоретических знаний по геометрии среди учащихся. Анализируя резльтаты опроса, можно сделать вывод, что данную тему нужно изучать и говорить о ней. Мы рекомендуем наш проект использовать на уроках геометрии и ОБЖ.










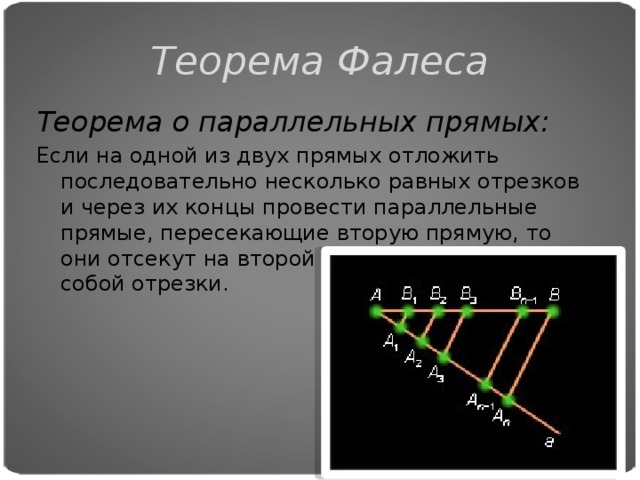
![Задача Фалеса Разделить данный отрезок AB на n равных частей. Построение. Пусть [ AB ] – данный отрезок. Проведем из точки A луч a , не содержащий отрезок AB . Отложим от точки A на построенном луче равные отрезки: AA 1 , A 1 A 2 , ... , A n – 1 A n . Соединим точки A n и B . Проведем через точки A 1 , A 2 , ... , A n – 1 прямые, параллельные прямой A n B . Они пересекают отрезок AB в точках B 1 , B 2 , ... , B n – 1 . Отрезки AB 1 , B 1 B 2 , ... , B n – 1 B – искомые отрезки.](https://fsd.kopilkaurokov.ru/uploads/user_file_53c9366d3d080/img_user_file_53c9366d3d080_10.jpg)