Открытый урок по математике в 6 классе на тему " Комбинаторика"

Технология проведения

Деятельность

учеников

Деятельность

учителя

Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов

УУД

I. Мотивация к учебной деятельности

Цели: -проверка готовности обучающихся, их настроя на работу

Подготовка учащихся к уроку. Отвечают на вопрос: комбинаторика - ветвь математики, изучающая комбинации и перестановки предметов, возникла в ХII веке.

Организует учащихся. Проверяет готовность обучающихся к уроку, настраивает на работу.

• Здравствуйте, ребята!

• В курсе математики 5-го класса и на прошлом уроке мы познакомились с таким разделом математики как комбинаторика. Вспомните, что такое комбинаторика? СЛАЙД 2.

• Очень часто в жизни приходится делать выбор, принимать решение. Это сделать очень трудно не потому, что его нет или оно одно и поэтому его трудно найти, а потому, что приходится выбирать из множества возможных вариантов, различных способов, комбинаций.

• И нам всегда хочется, чтобы этот выбор был оптимальный.

• Задачи, которые мы сегодня будем решать, помогут вам творить, думать необычно, оригинально, смело, видеть то,

мимо чего вы часто проходили не замечая, любить неизвестное, новое; преодолевать трудности и идти через невозможное вперед.

Девизом нашего урока сегодня станет древняя китайская мудрость: СЛАЙД 3

Скажи мне – и я забуду,

Покажи мне – и я запомню,

Вовлеки меня – и я запомню.

Личностные: самоопределение;

Регулятивные: целеполагание;

Коммуникативные:планирование учебного сотрудничества с учителем и сверстниками

II Актуализация знаний

Цель: обобщить знания по теме

Устная работа.

Отвечают на вопросы учителя

(с историей развития комбинаторики учащиеся познакомились на предыдущем уроке. Приложение 1.)

Организует устную работу. Следит за правильностью рассуждений.

• Когда возникла комбинаторика?

• Где применялись комбинаторные задачи?

• Назовите фамилии ученых, которым принадлежат первые научные исследования в области комбинаторики?

• Может ли комбинаторика помочь в реальной жизни?

• Как часто люди комбинируют что-либо?

• Какими способами мы умеем решать комбинаторные задачи? (перебор, дерево возможны вариантов, правило треугольника, правило умножения и др.)

• В чем заключается правило решения задач с помощью дерева вариантов?

• Решите задачу, составив дерево возможных вариантов: Из чисел 1,5, 9 составить трехзначные числа, при условии, что цифры не должны повторяться. Сколько получится чисел? СЛАЙД 4.

• В чем заключается правило умножения?

• У вас на парте лежат полоски красного, белого и синего цвета. Соберите, пожалуйста, флаг Российской Федерации.

• Как вы расположили полоски?

• А какое значение имеют цвета флага нашей страны?

(белый - благородство, синий – честность, красный – смелость) СЛАЙД 5

• Флаги каких стран также состоят из полос красного, белого, синего цвета? (Франции, Голландии) СЛАЙД 6

• Они отличаются от флага России? Чем? (расположением полос)

• Замечательно, что вы хорошо знаете флаг своей Родины!

• Интересно, сколькими способами можно составить

флаг из горизонтальных и вертикальных полос белого, красного и синего цвета? Решите задачу с помощью правила умножения. СЛАЙД 7.

Личностные: умение структурировать знания, выбор наиболее эффективных способов решения задания, умение осознанно и произвольно

Регулятивные: целеполагание;

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками

III Решение задач

1) Работа в группах

Цели:-. Составление плана работы

2) Работа с интерактивной доской

Разбиваются в группы.

Ставят цели, формулируют (уточняют) план работы

Ставят цели, формулируют (уточняют) способы выполнения работы

Уточняет понимание учащимися поставленных целей урока.

Выдвигает проблему.

Организует: проверку выполнения упражнения; беседу по уточнению знаний; оценочные высказывания обучающихся; обсуждение способов решения;

Класс разбивается на пять групп. Каждой группе предлагается решить задачу и представить ее решение на доске для остальных групп. (Приложение 2).Повторяют правила работы в группе СЛАЙД 8.

1 группа. Участники лыжных соревнований стартуют с интервалом в 30 секунд. Чтобы определить порядок старта, спортсмены тянут жребий, указывающий номер старта. Сколько существует различных последовательностей выхода лыжников на старт, если в соревнованиях принимают участие 6 лыжников? Через какой промежуток времени все спортсмены будут на лыжне?

2 группа. Проказница-Мартышка,

Осел, Козел,

Да косолапый Мишка

Затеяли квартет.

Ударили в смычки,

дерут, а толку нет.

«Стойте, братцы, стой! –

кричит Мартышка.

– Погодите!

Как музыке идти?

Ведь Вы не так сидите…»

Сколькими различными способами могут музыканты, герои басни И. А. Крылова, сесть в один ряд?

3 группа. В субботу в 6 классе 5 уроков: физкультура, русский язык, литература, ИЗО, математика. Сколько можно ставить вариантов расписания на день? Сколько можно составить вариантов расписания на день, зная, что математика – последний урок?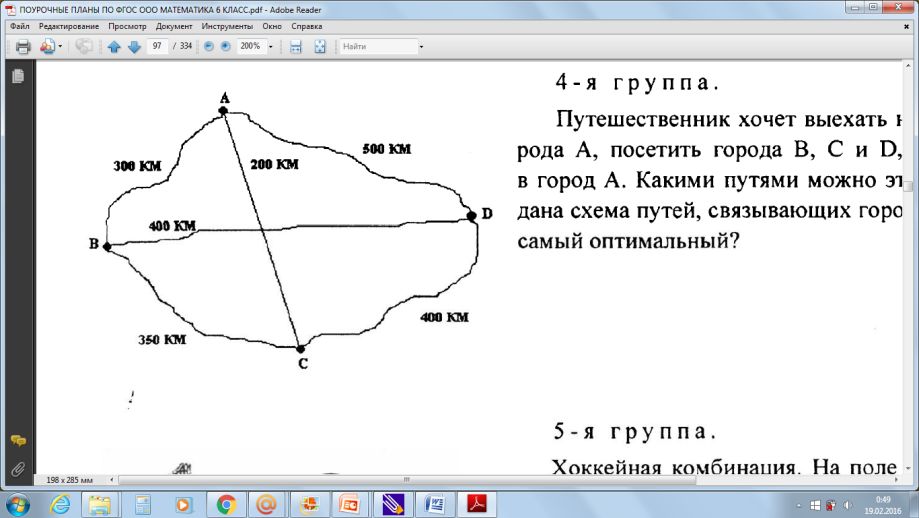

4 группа. Путешественник хочет выехать на своей машине из города А, посетить города В, С и D, после чего вернуться в город А. Какими путями можно это сделать? На рисунке дана схема путей, связывающих города. Какой из вариантов самый оптимальный?

5 группа. Хоккейная комбинация. На поле 5 игроков. Начал комбинацию игрок № 1, продолжили игроки с другими номерами, а забил гол игрок № 5. Каждый хоккеист ударил по шайбе только один раз. На рисунке с помощью стрелок изображен один из возможных вариантов передачи шайбы между игроками в данной комбинации. Изобразите все другие возможные варианты передачи шайбы.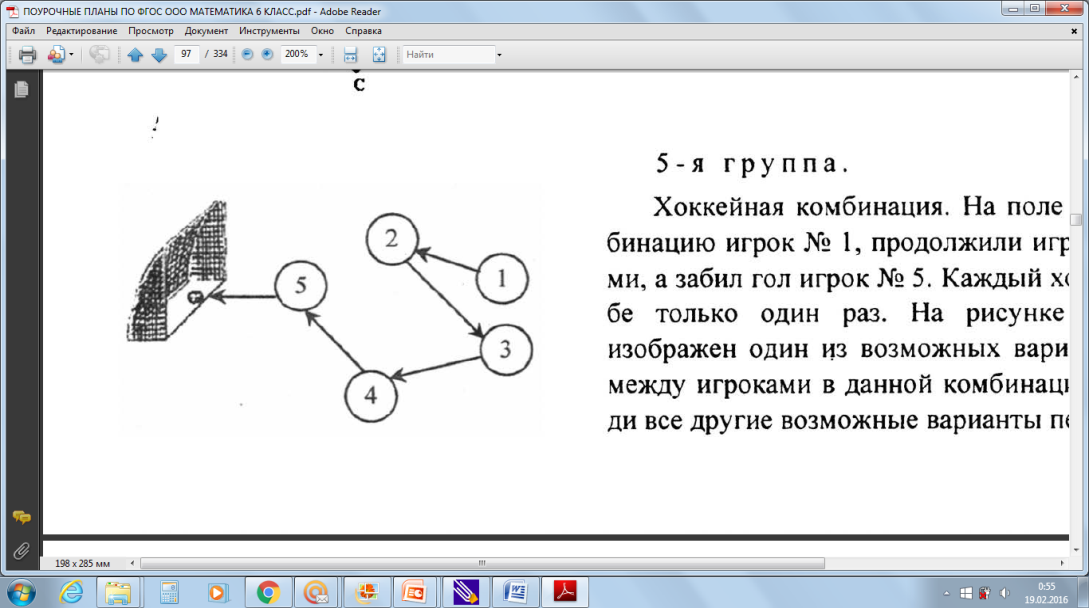

Решение:

1-я группа.

Первому лыжнику достанется 6 вариантов выбора номера. Второму – 5 и т. д.

Итого: 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 720. Все лыжники будут на лыжне через 150 с, то есть через 2,5 мин.

2-я группа.

Всего вариантов может быть 4 ∙ 3 ∙ 2 ∙ 1 = 24.

3-я группа.

1. Всего расписаний на день можно составить 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 120.

2. Если математика стоит последней, то всего расписаний 4 ∙ 3 ∙ 2 ∙ 1 = 24.

4-я группа.

Маршрут ABCDA = 300 + 350 + 400 + 500 = 1500

Маршрут ACDBA = 200 + 400 + 400 + 300 = 1300

Маршрут ACBDA = 200 + 350 + 400 + 500 = 1450

Маршрут ABDCA = 300 + 400 + 400 + 200 = 1300

Маршрут ADBCA = 500 + 400 + 350 + 200 = 1450

Ответ: Самый оптимальный маршрут ACDBA или ABDCA.

5-я группа.

Если игроки под номерами 1 и 5 неизменны, то меняем местами игроков с номерами 2, 3, 4. Таких комбинаций возможно 6. Значит, всего 7 комбинаций

Фронтальная работа класс на интерактивной доске с цифровым образовательным ресурсом Комбинаторика-1 http://files.school-collection.edu.ru/dlrstore/10e5a6e1-3646-45dd-8078-7a4f1e41b1d7/%5BA79_07-01-KT05%5D_%5BQS_00%5D/%5BA79_07-01-KT05%5D_%5BQS_00%5D.html

Правильные ответы:

Познавательные: самостоятельное выделение-формулирование познавательной цели, формулирование проблемы.

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками

Регулятивные: целеполагание

Личностные: умение структурировать знания, выбор наиболее эффективных способов решения задания, умение осознанно и произвольно

Регулятивные: целеполагание;

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками

IV. Самостоятельная работа

Цель:

-осознание каждым обучающимся степени овладения знаниями

Осуществляют: самооценку; самопроверку; взаимопроверку; предварительную оценку.

Контролирует выполнение работы.

Осуществляет:

-индивидуальный контроль;

-выборочный контроль.

Организует: проверку выполнения упражнения; беседу по уточнению знаний; оценочные высказывания обучающихся; обсуждение способов решения;

Физкультминутка. Раз, два, три, четыре, пять –

СЛАЙД 9. Все умеем мы считать.

Раз! Подняться, потянуться.

Два! Согнуться, разогнуться.

Три! В ладоши три хлопка,

Головою три кивка.

На четыре – руки шире.

Пять – руками помахать.

Шесть - за парту мы присели.

Значит, хватит отдыхать!

Самостоятельная работа. (работа с учебником)

СЛАЙД 10.

Вариант 1. № 504 Ответ: 64, 24

Вариант 2. № 506 Ответ: 48, 18

Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.

Личностные: самоопределение

V. Рефлексия

Цели:- соотнесение поставленных задач с достигнутым результатом

Формулируют конечный результат своей работы на уроке.

Отмечает степень вовлеченности учащихся
в работу на уроке.

Притча. СЛАЙД 11.

Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал вопрос каждому. У первого спросил: «А что ты делал целый день?». И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнил свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»

- Ребята! Давайте мы попробуем с вами оценить каждый свою работу за урок.

- Кто работал как первый человек?

- Кто работал добросовестно?

- Кто принимал участие в «строительстве храма»?

В конце урока подводится итог работы, уровень достижения цели:

• Сегодня на уроке я научился:

• Мне было интересно…

• Мне было трудно:

• Я понял, что:

• Больше всего мне понравилось (не понравилось):

• Своей работой на уроке я доволен (не совсем, не доволен), потому что:

Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли.

Познавательные: рефлексия

Личностные: смыслообразование

Дает комментарий к домашнему заданию.

Домашнее задание: СЛАЙД 12. придумать комбинаторную задачу прикладного характера; решить № 503, 514.