Решение задач по теме
«Практическое применение объемов многогранников»»
Цели урока:
Закрепить умение решать задачи на вычисление объемов многогранников.
Показать практическое применение математических знаний в жизни.
Развивать пространственное воображение, интерес к предмету
Оборудование: компьютер, проектор, экран
Ход урока.
Организационный момент.
Тема нашего урока Практическое применение объемов многогранников. Откройте, пожалуйста, тетради, запишите число, классная работа, тема урока. В этом году вы оканчиваете школу, вам предстоит выбрать профессию, и вы должны знать, как вам может помочь геометрия в вашей профессиональной деятельности. Сегодня на уроке мы рассмотрим , как на практике можно использовать полученные вами знания по теме «Объемы многогранников».
Повторение и систематизация пройденного материала.
Фронтальный опрос, но сначала давайте вспомним
Перечислите свойства объема.
По какой формуле вычисляется объем прямоугольного параллелепипеда?
Назовите формулу, с помощью которой мы можем найти объем куба.
По какой формуле вычисляется объем прямой призмы? V = Sосн H
H
Решение задач устно. Представьте, что вы находитесь на строительной площадке, работаете прорабом. Вам привезли кирпичи, сложенные в штабели
Как определить количество кирпичей, сложенных в штабель прямоугольной формы, если все кирпичи уложены в одну сторону?
Вы шеф – повар детского санатория. Вам выдали кусок масла в виде куба со стороной 15см.Вы должны разрезать его на маленькие кубики с ребром 3 см.Хватит ли вам этого масла, чтобы получилось 112 порций? /125/.
Вы директор продуктовой базы. Завод – производитель предложил вам определенное количество мороженого с большой скидкой. Как вы сможете определить полезную емкость 4-камерного ледяного склада, если каждая камера имеет форму прямоугольного параллелепипеда с внутренними размерами 6×5×3? /360 м3/.
Работа по карточкам.
Проверка работ по карточкам.
Мыслитель древности П. Рамус сказал: «Геометрия - это наука хорошо измерять».
Многогранники и тела вращения имеют широкое распространение в окружающем нас мире. Геометрия вышла из практических нужд человека, связанных с измерением земельных участков, вычислением площадей и объёмов фигур. Этот мир геометрии окружает нас с самого рождения. Ведь всё, что мы видим вокруг: прямоугольник - окна, дома-параллелепипеды, загадочный узор снежинки, капля воды – всё так или иначе относится к геометрии, ничто не ускользает от её внимательного взгляда. Вспомним известные архитектурные изображения.
Слайд Александрийский маяк. В 285 году до н.э.на острове Фарос архитектор Сострат Книдский приступил к строительству маяка. Маяк строился пять лет и получился в виде трехэтажной башни высотой 120 метров. В основании он был квадратом со стороной тридцать метров, первый 60-метровый этаж башни был сложен из каменных плит и поддерживал 40-метровую восьмигранную башню, облицованную белым мрамором. На третьем этаже, в круглой, обнесенной колоннами башне, вечно горел громадный костер, отражавшийся сложной системой зеркал.
Египетские пирамиды. Почти пять тысяч лет стоит эта огромная пирамида. Высота её достигала 147 м (сейчас из-за обвала вершины её высота равна 137 м), а каждая из сторон по длине составляет 233 м. Для того чтобы обойти пирамиду Хуфу кругом, нужно пройти около километра. Вплоть до конца XIX в. пирамида Хуфу являлась самым высоким сооружением на земле. Её грандиозные размеры поражали всех, кто был в Египте. Недаром первые русские путешественники, попавшие в Египет, называли пирамиды "рукотворными горами".
Башня Сююмбике. Главная достопримечательность казанского Кремля - семиярусная проездная башня Сююмбике высотой 58 метров
Она относится к «падающим» башням (как, например, Пизанская башня), так как имеет заметный наклон в северо-восточную сторону. На сегодняшний день отклонение её шпиля от вертикали составляет 1,98 м
Башня построена царицей Сююмбике в память своего мужа Сафа-Гирея, умершего в 1549 году.
Мечеть Кул-Шариф Кул-Шариф - главная мечеть Казани и Татарстана. Расположена в западной части Кремлевского комплекса, во дворе бывшего Юнкерского училища. Самая высокая в Европе. Ориентация мечети на Мекку была определена с точностью до сотой доли секунды через спутник. 57-метровые минареты уступают по высоте главному символу Казанского кремля - башне Сююмбике всего два метра. По замыслу архитекторов купол напоминает "казанскую шапку" - корону казанских ханов, которая хранится в Оружейной палате в Москве.
Но наши дома должны быть не только красивы, но и удобны для жителей. Когда человеку уютно, приятно, спокойно, он говорит что ему комфортно.
Оказывается, комфортность определяется формой помещения, его линейными размерами. Коэффициент комфортности можно найти по формуле:
K = 36πV2 / S3 , где K – изопериметрический коэффициент комфортности, V – объем жилища, S – полная поверхность жилища, включая и пол. Если вам предстоит работать в риэлтерской фирме, то эта формула может стать настоящим помощником при продаже жилья.
И чем меньше этот коэффициент, тем комфортнее жилище. Сейчас мы найдем коэффициент комфортности этого кабинета
Решение задач.
Кабинет имеет линейные размеры 6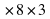 м3.Найти коэффициент комфортности.
м3.Найти коэффициент комфортности.
Решение: К = 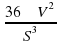
V = 6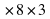 = 144 м3
= 144 м3
S = 2Sосн + РН
S = 2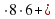 (8 + 6)
(8 + 6) 2
2  3 = 96 + 84 = 180( м2 )
3 = 96 + 84 = 180( м2 )
К = 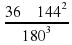 = 0,401
= 0,401
Ответ: 0,4
Домашнее задание: вычислить коэффициент комфортности своей квартиры покомнатно.
Скажите, пожалуйста, ребята, как вы думаете, представителю какой профессии может быть полезна эта формула? (архитектору, риэлтору)
Строителям необходимо вырыть канал. Перпендикулярное сечение канала – равнобедренная трапеция с основаниями 6м и 14м. Участок канала между шлюзами длиной 2км вмещает 6 104 м3 воды. Определите глубину канала.
104 м3 воды. Определите глубину канала.

Решение: рассмотрим прямой параллелепипед, в основании которого равнобедренная трапеция. Высота параллелепипеда – это длина между шлюзами 2км. Объем 6 104 м3. Требуется найти высоту трапеции. V = Sосн
104 м3. Требуется найти высоту трапеции. V = Sосн H
H
Sосн = 6 104 м3 : 2км = 6
104 м3 : 2км = 6 104 : 2000 = 30м2.
104 : 2000 = 30м2.
h=30: (6 + 14) 2 = 3м.
2 = 3м.
ответ: 3м.
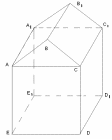 Какое количество зерна вмещает склад, имеющий размеры пола 8м*30 м, максимальная высота склада 5м, минимальная высота склада 3м.Плотность зерна 666 кг/куб.м
Какое количество зерна вмещает склад, имеющий размеры пола 8м*30 м, максимальная высота склада 5м, минимальная высота склада 3м.Плотность зерна 666 кг/куб.м
Решение:
Дано: пятиугольная призма,
ED=8 м, DD1=30м, BH=5м, CD=3м, ρ=666 кг/м3
Найти: m
Решение: V=Sосн∙H, Sосн= Sпрям+ S
Sпрям=3∙8=24 (м2), 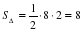 (м2), Sосн=24+8=32(м2),
(м2), Sосн=24+8=32(м2),
V=32∙30=960 м3,
m= ρ∙V, m=666∙960=639360 кг=639,36 т.
Ответ: 639,36 т.
А в заключение я хочу сказать: «Если у вас плохое настроение, вы устали, возьмите интересную геометрическую задачу, сделайте большой и красивый чертёж и …». Поверьте, хорошая геометрическая задача может прекрасно заменить самого лучшего психотерапевта.
Вариант 1 Фамилия_________________________________________
Выберите неверное утверждение.
За единицу измерения объемов принимается куб, ребро которого равно единице измерения отрезков;
Тела, имеющие равные объемы, равны;
Объем прямоугольного параллелепипеда равен произведению трех его измерений;
Объем куба равен кубу его ребра.
Площадь полной поверхности куба равна 150см2. Найдите объем куба.
150см3 b)25см3 c)250 см3 d)105 см3 e)125 см3
Как изменится объем правильной четырехугольной призмы, если ее высоту увеличить в n раз?
Не изменится; Увеличится в n раз; Уменьшится в n раз; Уменьшится в 2n раз.
Запишите формулу для вычисления площади полной поверхности прямой призмы
Запишите формулу для вычисления площади прямоугольника
________________________________________________
Вариант 2.Фамилия________________________________________
Выберите верное утверждение.
За единицу измерения объемов принимается квадрат, сторона которого равна единице измерения отрезков;
Если тело составлено из нескольких тел, имеющих общие внутренние точки, то его объем равен сумме объемов этих тел;
Объем прямоугольного параллелепипеда равен произведению трех его измерений на длину диагонали параллелепипеда;
Равные тела имеют равные объемы.
Объем куба равен 27м3. Найдите площадь полной поверхности куба.
36 см2;
9 см2;
108 см2;
27 см2;
54 см2.
Как изменится объем правильной четырехугольной призмы, если ее высоту уменьшить в n раз?
Не изменится;
Увеличится в n раз;
Уменьшится в n раз;
Уменьшится в 2n раз.
Запишите формулу для вычисления площади полной поверхности прямоугольного параллелепипеда
_________________________________________________________________
Запишите формулу для вычисления площади трапеции
___________________________________________________
![]()
 B Н C
B Н C
А D
Объем призмы.
49. Что значит, измерить объём тела? /Выразить его числом/.
50. Почему мы считаем, что объёмы двух одинаковых спичечных коробков равны?
51. Из скольких кубиков с ребром 3 см каждый можно составить куб с ребром 15 см2 ? /125/.
52. Определите полезную емкость 4-камерного ледяного склада на 60 т, если каждая камера имеет форму прямоугольного параллелепипеда с внутренними размерами 6×5×3. /360 м3/.
53. Как определить количество кирпичей, сложенных в штабель прямоугольной формы?
54. Два свинцовых куба с ребрами 6 см и 5 см переплавлены в один куб. Определите ребро этого куба. /7 см/.
55. Объём куба 27 м3. Найти его поверхность. /54 м2/.
56. Найдите ребро такого куба, у которого полная поверхность и объем численно равны. /6/.
57. Поверхность куба 150см2. Найдите его объем. /125 м3/.
Объем пирамиды
69. Сколько достаточно иметь данных, чтобы определить объём правильной четырехугольной пирамиды. /2/.
70. Диагональное сечение правильной четырехугольной пирамиды – равносторонний треугольник со стороной 6 см. Найти объём пирамиды. /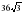 /.
/.
71. Определите объём правильной четырехугольной пирамиды, каждое ребро которой равно 6 см. /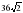 см/.
см/.
72. Сколько можно построить правильных пятиугольных пирамид заданного объема, зная высоту пирамиды? /Одну/.
73. Равновелики ли две пирамиды с равными высотами, если их основаниями являются четырехугольники с соответственно равными сторонами?
/Нет/.
Как сказал мыслитель древности П. Рамус: «Геометрия это наука хорошо измерять». Мы продолжим сегодня измерять цилиндр и покажем, что целесообразно измерить в той или иной ситуации, и зачем это нужно делать.
На прошлом уроке группа учащихся получила следующее задание: Молокозавод решил сделать новую, более экономичную упаковку для молока. Требуется сделать пакет для 1 литра молока, истратив на это как можно меньше материала. Какой формы пакет выгоднее сделать? Предложены следующие варианты: в форме куба, в форме шара, в форме цилиндра с квадратным осевым сечением, в форме конуса с осевым сечением в виде правильного треугольника, в форме правильного тетраэдра.
Итог урока.
1). Вопросы к учащимся: Что делали вы на уроке?
Что было самым интересным?
Что было главным на уроке?
Что понравилось?
. На столе находятся модели геометрических тел, накрытые скатертью. Это различного вида призмы, параллелепипеды, пирамиды, конусы, цилиндры, шары, сферы.
Вызываются к доске по одному человеку от каждой команды (обычно это студенты базового уровня знаний) и предлагается осмотреть набор моделей в течение одной минуты. После осмотра набор моделей вновь накрывается скатертью. Играющие должны выполнить “инвентаризацию”, то есть записать на доске названия фигур и выполнить от руки их изображения. (На составление списка и выполнение изображений отводится 3-4 минуты
I. Кто быстрее?
А) Слова на букву «К»
1.Геометрическая фигура.
2.Произведение гипотенузы на косинус прилежащего угла.
3.Прямая, имеющая с окружностью только одну общую точку.
4.Отношение прилежащего катета к гипотенузе.
Б) Слова на букву «П»
1)Наука, изучающая свойства фигур на плоскости.
2)Если 36см2 = S кв, то 24 см - ?
3)Геометрическая фигура, все углы которой равны.
4)Отрезок, соединяющий основание наклонной и перпендикуляра.
II. Кто больше? (За 2 мин записать формулы для вычисления площади
треугольника и прямоугольника).
Решить задачи.
1.В шар радиуса R вписан прямоугольный параллелепипед, диагональ которого составляет с одной из граней угол α , угол между диагональю этой грани и стороной основания 60°.Найдите объем параллелепипеда.
(R3√3cosαsin2α)
2.В прямоугольном параллелепипеде помещены 2 шара радиуса k так, что каждый касается другого шара и пяти граней параллелепипеда. Найдите объем параллелепипеда. (16k³)
УЭ – 8 Самостоятельная работа (по вариантам).
I вариант
1) Объем прямоугольного параллелепипеда равен 96 см³, боковое ребро 8 см.
Чему равна площадь основания?
2) Диагонали куба 20 см. Найдите объем куба.
3) Основанием прямого параллелепипеда является квадрат со стороной 8√2 см. Диагональ боковой грани образует с плоскостями оснований угол α. Найдите объем параллелепипеда.
II вариант
1) Объем прямоугольного параллелепипеда равен 100 см³, площадь основания 25 см². Найдите высоту параллелепипеда.
2) Диагональ куба равна 10 см. Найдите объем куба.
3) В прямоугольном параллелепипеде основанием является квадрат. Диагональ параллелепипеда равна 6 дм и образует угол α с боковым ребром, имеющим с ней общее начало. Найдите объем прямоугольного параллелепипеда.
V = 6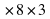 = 144 м3
= 144 м3
S = 2Sосн + РН
S = 2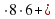 (8 + 6)
(8 + 6) 2
2  3 = 96 + 84 = 180( м2 )
3 = 96 + 84 = 180( м2 )
К = 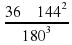 = 0,401
= 0,401
Ответ: 0,4

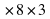 м3.Найти коэффициент комфортности.
м3.Найти коэффициент комфортности.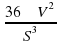
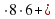 (8 + 6)
(8 + 6)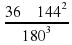 = 0,401
= 0,401
 Какое количество зерна вмещает склад, имеющий размеры пола 8м*30 м, максимальная высота склада 5м, минимальная высота склада 3м.Плотность зерна 666 кг/куб.м
Какое количество зерна вмещает склад, имеющий размеры пола 8м*30 м, максимальная высота склада 5м, минимальная высота склада 3м.Плотность зерна 666 кг/куб.м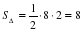 (м2),
(м2), 
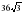 /.
/.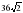 см/.
см/.















