ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ТВЕРСКОЙ ОБЛАСТИ
«ОСТАШКОВСКИЙ ТЕХНИКУМ»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
ОТКРЫТОГО ЗАНЯТИЯ
По дисциплине: «МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ»
Раздел: Линейное программирование
Тема: «Методы решения задачи о назначениях».
Специальность: 230115 Программирование в компьютерных системах
Курс: 3
(базовый уровень подготовки)
Осташков, 2014
Автор – составитель:
преподаватель дисциплины «Математическое программирование»
Суркова Марина Владимировна
Рецензенты:
Потоцкая Е.А., зам.директора по УР ГБОУ СПО «Осташковский техникум»
Власова Т.Н., преподаватель Осташковского финансово-экономического колледжа (филиал Финансового университета при Правительстве РФ)
Содержание
Пояснительная записка 6
Учебно – методический план занятия 7
Структурный план хода занятия 10
Приложение №1. Входной контроль 12
Приложение №2. Изучение нового материала 14
Приложение №3. Осмысление полученных знаний. 19
Пояснительная записка
Методическое пособие разработано для преподавателя с целью формирования знаний по теме «Методы решения задачи о назначениях», в процессе теоретического занятия студенты получают знания о математических методах решения задач линейного программирования, которые им необходимы для формирования практических умений.
Методическая разработка составлена в соответствии с требованиями к знаниям по ФГОС III поколения, для использования на теоретическом занятии в рамках специальности 230115 «Программирование в компьютерных системах».
В соответствии с ФГОС, после изучения данной темы студент должен:
Методическая разработка состоит из «Пояснительной записки», «Учебно-методического плана», «Структурного плана хода занятия», «Входной контроль» (приложение №1), «Изложение нового материала» (приложение №2), «Закрепление материала» (приложение №3).
Учебно – методический план занятия
Тема занятия: Методы решения задачи о назначениях.
Продолжительность проведения занятия 45 минут.
Мотивация темы: Данная тема является основой для дальнейшего усвоения учебного материала.
Вид:
Форма обучения:
Методы обучения:
словесный;
наглядный;
практический;
дедуктивный
Внутрипредметные связи:
Цели занятия:
Образовательная:
Развивающая:
развивать навыки построения и классификации моделей задач линейного программирования;
развивать навыки логического мышления;
развивать навыки применения теоретического материала при решении практических заданий.
Воспитательная:
способствовать формированию таких личностных качеств как внимательность, наблюдательность, самостоятельность;
повышение культуры математической речи.
Средства обучения:
Компьютер.
Мультимедийный проектор.
Экран.
Презентация по теме занятия «Задача о назначениях».
Презентация по теме "Использование MS Excel при решении задач линейного программирования" (для внеаудиторной работы студентов).
Формируемые компетенции: ОК 2; ОК 3; ОК 4; ОК 5; ОК 6; ОК 9.
Междисциплинарная интеграция:
Внутридисциплинарная интеграция:
М![Прямая соединительная линия 3]()
етодическое обеспечение занятия: Тематический кроссворд (для проведения входного контроля), содержание учебного материала, презентация «Задача о назначениях», контрольные вопросы, презентация «Брейн-ринг. Шоу-игра», презентация «Решение ЗЛП с использованием MS Excel» .
Домашнее задание:
Подготовка реферата (презентации) по теме «История возникновения и развития методов линейного программирования».
Задания для внеаудиторной работы студентов:
Сведение задачи о назначении к каноническому виду ЗЛП и решение её симплексным методом с использованием MS Excel.
Перечень литературы:
Основная:
1. Абчук В. А. Экономико-математические методы: Элементарная математика и логика. Методы исследования операций. — СПб.: Союз, 2009.
2. Грешилов А.А. Как принять наилучшее решение в реальных условиях. - М.: Радио и связь, 2010.
2. Канторович Л.В. Экономический расчёт наилучшего использования ресурсов. – М.: Наука, 2011.
Дополнительная:
1. Сдвинков О.А. математика в MS Excel 2002- М. Солон-Пресс, 2009
Структурный план хода занятия
| № | Основные этапы занятия. Коды формируемых компетенций | Ориентировочное время | Содержание этапа. Методическое обоснование |
| 1. | Организационный момент Цель: этап дисциплинирует и настраивает студентов на учебную деятельность | 2 мин. | Преподаватель отмечает отсутствующих на занятии, проверяет готовность аудитории и студентов к занятию |
| 2. | Мотивация учебной деятельности. Целевая установка. Формирование ОК 2. Цель: Активизация внимания студентов к изучению нового метода. | 3 мин. | Преподаватель подчеркивает значимость, актуальность темы. Определяет цели и план занятия. |
| 3. | Входной контроль (приложение №1) Цель: проверить состояние знаний обучающихся по изученному ранее материалу. | 7 мин. | Студенты фронтально отгадывают предложенный преподавателем кроссворд с использованием компьютерной техники. |
| 4. | Изложение нового материала (приложение №2) ОК 3, ОК 4 Цель - сформировать знания об алгоритме выполнения венгерского метода. | 15 мин.
| Совместно с преподавателем студенты создают опорный конспект лекции. Преподаватель использует презентацию по теме занятия. |
| 5. | Осмысление полученных знаний (приложение №3): ОК 4 Цель: систематизировать и закрепить полученные знания | 10 мин. | Закрепление материала осуществляется путем ответов на контрольные вопросы в шоу игре «Брейн-ринг» с использованием компьютерной техники.
|
| 6. | Подведение итогов
| 3 мин. | Обсуждаются итоги работы студентов и выставляются оценки с комментариями. Оценка выставляется с учетом всех этапов занятия. |
| 7. | Задание на дом ОК 5; ОК 6; ОК 9 | 5 мин. | Подготовка реферата (презентации) по теме «История возникновения и развития методов линейного программирования». Задание для внеаудиторной работы студентов: Сведение задачи о назначении к каноническому виду ЗЛП и решение её симплексным методом с использованием MS Excel. |
|
| Всего | 45 мин |
|
Приложение №1. Входной контроль
Что включает в себя математическая модель любой задачи линейного программирования?
Ответы:
максимум или минимум целевой функции (критерий оптимальности);
требование не отрицательности переменных;
систему ограничений в форме линейных уравнений и неравенств;
Как привести открытую транспортную задачу к закрытому виду?
Ответ: ввести фиктивного поставщики или фиктивного потребителя с нулевой стоимостью перевозок.
Какие методы применяются для решения задачи линейного программирования и условия их применения.
Ответы:
графический (если число переменных задачи - 2);
симплексный (если задача представлена в каноническом виде).
Примечание: ответы на данный вопрос предполагаются в виде решения кроссворда (демонстрируется на экран).
Какие методы применяются для решения транспортной задачи?
Ответы:
метод потенциалов;
симплексный (при условии сведения её к ЗЛП).
Примечание: ответы на данный вопрос предполагаются в виде решения кроссворда (демонстрируется на экран).
5. Какой метод чаще всего используется для получения опорного (базисного) плана перевозок в транспортной задаче?
Ответ: метод потенциалов.
6. Назовите достоинства и недостатки симплексного метода.
Ответы:
достоинство: является универсальным методом, позволяет решать широкий круг задач.
недостаток: требует большого объема вычислений.
|
| - универсальный метод решения всех видов ЗЛП |
|
| - метод решения ЗЛП в случае 2-х переменных |
|
| - метод решения транспортной задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
|
|
|
| А |
|
|
|
|
|
|
|
|
|
|
|
| Ф |
|
|
|
|
|
|
|
|
|
|
|
| 9 |
|
|
|
|
|
|
|
|
|
|
|
| Ч |
|
|
|
|
|
|
|
|
|
|
|
| Е |
|
|
|
|
| 7 | И | М | П | Л | 2 | 8 | С | Н | Ы | Й |
|
|
|
|
|
|
|
|
| К |
|
|
|
|
|
| П | О | Т | 5 | 3 | Ц | И | А | Л | О | 1 |
|
|
|
|
|
|
|
| 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Метод решения задачи о назначении:
|
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
Приложение №2. Изучение нового материала
Задача о назначениях - частный случай транспортной задачи, в которой количество пунктов производства и потребления равны, т.е транспортная таблица имеет форму квадрата, а объем потребления и производства в каждом пункте равен 1.
Данная задача решается с помощью алгоритма, носящего название «Венгерского метода», состоящего из 3 этапов:
1 этап. Преобразование строк и столбцов матрицы.
Формализация проблемы в виде транспортной таблицы;
В каждой строке таблицы найти наименьший элемент и вычесть его из всех элементов данной строки;
Повторить ту же процедуру для столбцов.
Задачей является распределение всех подлежащих назначению единиц в клетки с нулевой стоимостью. Оптимальное значение целевой функции в этом случае равно нулю.
2 этап. Определение назначения.
1. Найти строку, содержащую только одно нулевое значение, в его клетку помещается один элемент (0 обводится квадратиком). Если такие строки отсутствуют, допустимо начать с любой строки.
2. Зачеркнуть оставшиеся нулевые значения данного столбца.
3. Повторять пп.1-2, пока продолжение указанной процедуры окажется невозможным. Если окажется, что имеется несколько нулей, которым не соответствуют назначения, и которые остались незачеркнутыми, необходимо:
4. Найти столбец, содержащий только одно нулевое значение, в его клетку помещается один элемент.
5. Зачеркнуть оставшиеся нули в данной строке.
6. Повторять пп.4-5, пока продолжение указанной процедуры окажется невозможным.
Если выяснится, что таблица содержит неучтенные нули - повторить пп. 1-6. Если решение является допустимым, оно оптимально. Если нет - перейти к этапу 3.
3 этап. Модификация преобразованной матрицы.
1. Провести минимальное количество прямых через столбцы и строки матрицы таким образом, чтобы они проходили через все нули, содержащиеся в таблице.
2. Найти наименьший из элементов, через которые не проходит ни одна прямая.
3. Вычесть его из всех элементов, через которые не проходят прямые.
4. Прибавить его ко всем элементам, лежащим на пересечении прямых.
5. Элементы, через которые проходит только одна прямая, оставить неизменными.
В результате в таблице появится как минимум одно новое нулевое значение. Вернуться к этапу 2 и повторить решение заново.
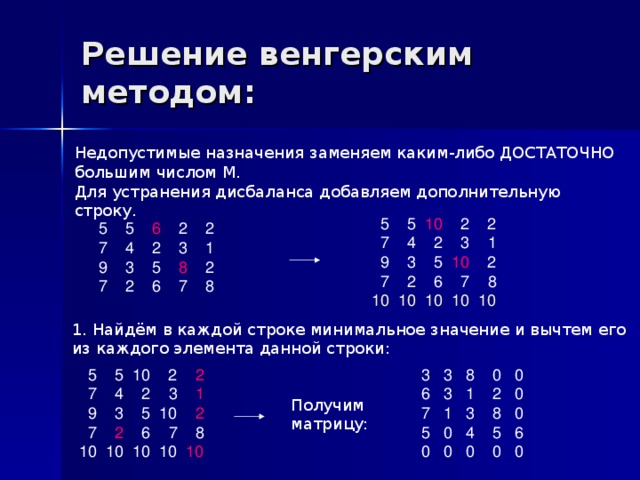
Следует иметь в виду, что для любого недопустимого назначения соответствующая ему стоимость условно полагается равной достаточно большому числу М в задачах на минимум. Если исходная матрица не является квадратной, то следует ввести дополнительно необходимое количество строк или столбцов, а их элементам присвоить значения, определяемые условиями задачи, возможно после редукции, а доминирующие альтернативы дорогие или дешевые исключить.
Пример решения задачи .
Задание. Рассматривается вычислительная система состоящая из n вычислительных машин. Имеется n задач. Задана матрица T определяющая время решения i-й задачи на j-м машине. Задачи решаются одновременно с некоторого момента t0. Найти такое распределение задач по вычислительным машинам, чтобы общее время решения всех задач было бы минимальным при условии что на одной машине может решаться только одна задача.
Решение.
Исходная матрица имеет вид:
| 5 | 5 | M | 2 | 2 |
| 7 | 4 | 2 | 3 | 1 |
| 9 | 3 | 5 | M | 2 |
| 7 | 2 | 6 | 7 | 8 |
Для устранения дисбаланса добавляем дополнительные строки.
1. Проводим редукцию матрицы по строкам. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.
| 3 | 3 | M | 0 | 0 | 2 |
| 6 | 3 | 1 | 2 | 0 | 1 |
| 7 | 1 | 3 | M | 0 | 2 |
| 5 | 0 | 4 | 5 | 6 | 2 |
| 0 | 0 | 0 | 0 | 0 | 0 |
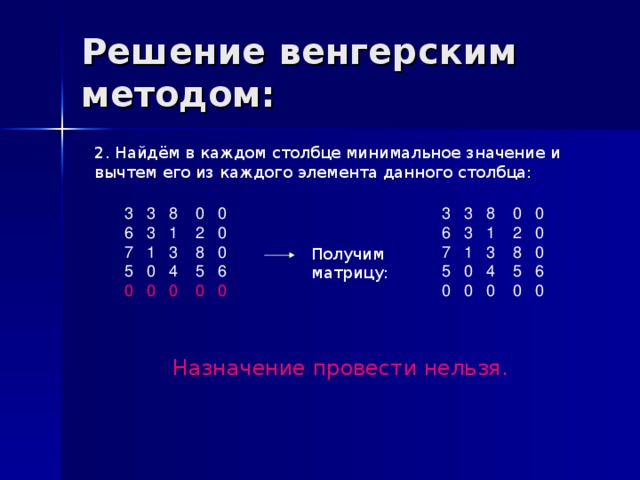
Затем такую же операцию редукции проводим по столбцам, для чего в каждом столбце находим минимальный элемент:
| 3 | 3 | M | 0 | 0 |
| 6 | 3 | 1 | 2 | 0 |
| 7 | 1 | 3 | M | 0 |
| 5 | 0 | 4 | 5 | 6 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
После вычитания минимальных элементов получаем полностью редуцированную матрицу.
2. Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость.
| 3 | 3 | M | [0] | [-0-] |
| 6 | 3 | 1 | 2 | [-0-] |
| 7 | 1 | 3 | M | [-0-] |
| 5 | [0] | 4 | 5 | 6 |
| [-0-] | [-0-] | [-0-] | [-0-] | [0] |
Поскольку расположение нулевых элементов в матрице не позволяет образовать систему из 5-х независимых нулей (в матрице их только 3), то решение недопустимое.
3. Проводим модификацию матрицы. Вычеркиваем строки и столбцы с возможно большим количеством нулевых элементов: строку 5, столбец 5, строку 1, столбец 2.
Получаем сокращенную матрицу (элементы выделены):
| 3 | 3 | M | 0 | 0 |
| 6 | 3 | 1 | 2 | 0 |
| 7 | 1 | 3 | M | 0 |
| 5 | 0 | 4 | 5 | 6 |
| 0 | 0 | 0 | 0 | 0 |
Минимальный элемент сокращенной матрицы (1) вычитаем из всех ее элементов:
| 3 | 3 | M | 0 | 0 |
| 5 | 3 | 0 | 1 | 0 |
| 6 | 1 | 2 | M | 0 |
| 4 | 0 | 3 | 4 | 6 |
| 0 | 0 | 0 | 0 | 0 |
Затем складываем минимальный элемент с элементами, расположенными на пересечениях вычеркнутых строк и столбцов:
| 3 | 4 | M | 0 | 1 |
| 5 | 3 | 0 | 1 | 0 |
| 6 | 1 | 2 | M | 0 |
| 4 | 0 | 3 | 4 | 6 |
| 0 | 1 | 0 | 0 | 1 |
2. Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость.
| 3 | 4 | M | [0] | 1 |
| 5 | 3 | [0] | 1 | [-0-] |
| 6 | 1 | 2 | M | [0] |
| 4 | [0] | 3 | 4 | 6 |
| [0] | 1 | [-0-] | [-0-] | 1 |
4. Определяем матрицу назначения Х, которая позволяет по аналогично расположенным элементам исходной матрицы (в квадратах) вычислить минимальную стоимость назначения.
| 3 | 4 | M | [0] | 1 |
| 5 | 3 | [0] | 1 | [-0-] |
| 6 | 1 | 2 | M | [0] |
| 4 | [0] | 3 | 4 | 6 |
| [0] | 1 | [-0-] | [-0-] | 1 |
Cmin = 2 + 2 + 2 + 2 + 0 = 8.
Приложение №3. Осмысление полученных знаний.
Относится ли задача о назначении к задачам линейного программирования? (Да, относится).
Если какое-то назначение не может быть выполнено изначально, то, как это отражается в исходной матрице? (В соответствующей ячейке проставляется какое-то большое число).
Если исходная матрица не является квадратной, то применим ли венгерский метод? (Да, если привести исходную матрицу к квадратному виду, дополнив её недостающей строкой или столбцом с нулевыми значениями).
