Государственное областное бюджетное
профессиональное образовательное учреждение
«ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»
Методическая разработка
урока математики
на тему
«Логарифмические неравенства ».
Выполнил:
преподаватель математики
Заварзина В.Г.
Липецк 2016 г.
Тема урока:
«Логарифмические неравенства».
Цели урока:
1. Образовательные
а) закрепить умения и навыки решения логарифмических неравенств,
с помощью изученных свойств;
б) сформировать умение использовать полученные теоретические знания для решения практических задач, умение выстраивать логические умозаключения и делать выводы.
2. Развивающие:
а) развитие профессиональных качеств обучающихся (умений применять полученные знания на практике);
б) развитие познавательных умений и мышления (выделять главное, анализировать, сравнивать, определять и объяснять понятия).
3. Воспитательные:
а) формирование коммуникативных компетенций (умение работать в группе, умение отстаивать свое мнение, умение выслушивать мнение других);
б) воспитание навыков самостоятельной работы;
в) воспитание дисциплинированности.
Задачи урока:
1.отработка навыка добывания знаний через практическую деятельность;
2.закрепить навыки работы в группе, умение представлять себя, умение 3.аргументированно отстаивать свое мнение и вести дискуссию;
4.формировать навыки освоения учащимися картины мира через изучение нового материала;
Тип урока: комбинированный
Вид урока: урок обобщения и систематизации:
Методические приемы:
-самостоятельная работа (работа с раздаточным материалом);
-практический- решение задач прикладной направленности.
Межпредметные связи: история
Оборудование и наглядные средства обучения: рабочие тетради, мультимедийный проектор, интерактивная доска, презентация, демонстрационный и раздаточный материал, задачник “Алгебра и начала математического анализа” (профильный уровень часть1, 2) под редакцией А. Г. Мордковича .
Методическая цель: активизировать мыслительную деятельность обучающихся.
Ход урока:
I.Организационный момент: подготовка студентов к уроку (проверка отсутствующих на уроке, наличие тетрадей, проверка готовности рабочих мест студентов и преподавателя, готовности студентов к работе.)
На первом этапе преподаватель приветствует студентов, проверяет готовность группы к работе.
II. Сообщение темы и целей урока.(слайд 1,2)
Вступительное слово преподавателя.
Я приветствую вас на сегодняшнем уроке. Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Тема урока: “Логарифмические неравенства ”. Сегодня мы повторим понятие логарифма числа, свойства логарифма, закрепим умения применять эти понятия при решении неравенств.
Эпиграфом урока являются слова М.В. Ломоносова:
“Математику уже затем учить надо, что она ум в порядок приводит”.
Цель нашего урока: закрепить умения и навыки решения логарифмических неравенств, с помощью изученных свойств.
Для того, чтобы показать свои знания по данной теме, вы должны быть настойчивыми, целеустремленными, т.е. уметь применять все приобретенные знания. Я желаю вам успешной работы.
III. Проверка домашнего задания
Историческая справка (было задано подготовить исторические сведения о логарифмах)
История логарифма
Принцип, лежащий в основе любой системы логарифмов, известен очень давно и может быть прослежен в глубь истории вплоть до древневавилонской математики (около 2000 до н.э.). В те времена интерполяция между табличными значениями целых положительных степеней целых чисел использовалась для вычисления сложных процентов. Гораздо позже Архимед (287-212 до н.э.) воспользовался степенями числа 108 для нахождения верхнего предела числа песчинок, необходимого для того, чтобы целиком заполнить известную в те времена Вселенную. Архимед обратил внимание на свойство показателей степеней, лежащее в основе эффективности логарифмов: произведение степеней соответствует сумме показателей степеней. 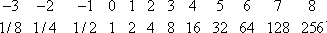
Приложения логарифмов(слайды 3,4,5)
Логарифмы первоначально использовались исключительно для упрощения вычислений, и это их приложение до сих пор остается одним из самых главных. Вычисление произведений, частных, степеней и корней облегчается не только благодаря широкой доступности опубликованных таблиц логарифмов, но и благодаря использованию т.н. логарифмической линейки – вычислительного инструмента, принцип работы которого основан на свойствах логарифмов. Линейка снабжена логарифмическими шкалами, т.е. расстояние от числа 1 до любого числа x выбрано равным log x; сдвигая одну шкалу относительно другой, можно откладывать суммы или разности логарифмов, что дает возможность считывать непосредственно со шкалы произведения или частные соответствующих чисел. Воспользоваться преимуществами представления чисел в логарифмическом виде позволяет и т.н. логарифмическая бумага для построения графиков (бумага с нанесенными на нее по обеим осям координат логарифмическими шкалами). Если функция удовлетворяет степенному закону вида y = kxn, то ее логарифмический график имеет вид прямой, так как
log y = log k + n log x
– уравнение, линейное относительно log y и log x. Наоборот, если логарифмический график какой-нибудь функциональной зависимости имеет вид прямой, то эта зависимость – степенная. Полулогарифмическая бумага (у которой ось ординат имеет логарифмическую шкалу, а ось абсцисс – равномерную шкалу) удобна в тех случаях, когда требуется идентифицировать экспоненциальные функции. Уравнения вида y = kbrx возникают всякий раз, когда некая величина, такая как численность населения, количество радиоактивного материала или банковский баланс, убывает или возрастает со скоростью, пропорциональной имеющемуся в данный момент количеству жителей, радиоактивного вещества или денег. Если такую зависимость нанести на полулогарифмическую бумагу, то график будет иметь вид прямой.
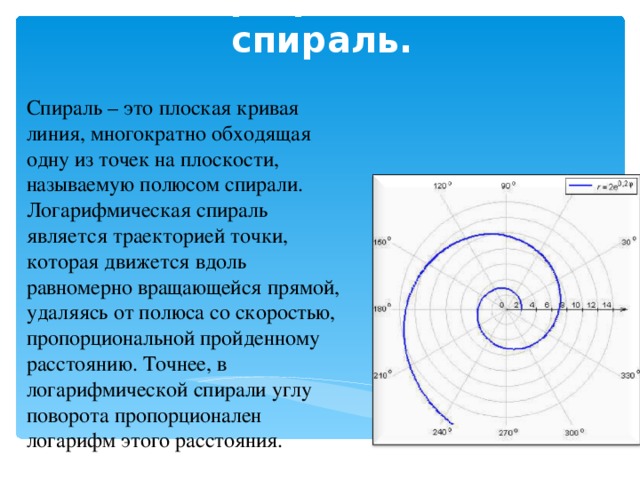
Логарифмическая функция возникает в связи с самыми разными природными формами. По логарифмическим спиралям выстраиваются цветки в соцветиях подсолнечника, закручиваются раковины моллюска Nautilus, рога горного барана и клювы попугаев.
Ребята, давайте проверим домашнее задание.(решение у доски в то время, пока рассказывают историческую справку)
№1.
а) log 10 100 = 2, т.к. 102 = 100 (определение логарифма и свойства степени),
б) log 5 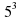 = 3
= 3
в) log 4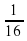 = –2
= –2
№ 2.
а) (32)log 3 7 = (7log 7 3)2 = 72 = 49 (степень степени, основное логарифмическое тожество, определение степени),
б) 7 2 log 7 3 = (7 log 7 3)2 = 32 = 9 (…),
в) 10 3 log 10 5 = (10 log 10 5)3 = 53 = 125 (…),
г) 0,1 2 log 0,1 10 = (0,1 log 0,1 10)2 = 102 = 100 (…).
Преподаватель.
Объясните своё решение.
IV. Систематизация и обобщение знаний.
Мы знаем, что слово логарифм происходит от греческого λόγοφ (число) и αρіμοφ (отношение) и переводится как отношение чисел. Это понятие ввел английский математик Джон Непер.
Дайте определение логарифма числа. (слайд 6). Ребята отвечают на вопросы.
1. Приведите пример для вычисления логарифма. (слайд 7)
2. Вычислите данный логарифм. На доске (log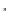 (-3)=; log
(-3)=; log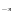 3=)
3=)
3. Дайте определение десятичного логарифма.
4. Перечислите основные свойства логарифмов.
5. Какие основные правила используют при вычислении логарифмов?
Правильные ответы студентов.
Логарифмом положительного числа b по положительному и отличному от 1 основанию a называют показатель степени, в которую нужно возвести число a, чтобы получить число b.
1. Пример:
lg 100000000=lg10 =8
=8
2. log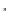 (-3)= решений нет.
(-3)= решений нет.
log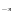 3= решений нет.
3= решений нет.
Данные логарифмы решений не имеют, т.к. отрицательные числа при логарифме и основание быть не могут.
3. Логарифм по основанию 10 называют десятичным логарифмом.
4. Основные свойства логарифмов
loga x + loga y = loga (x · y);
loga x − loga y = loga (x : y).
Сумма логарифмов равна логарифму произведения, а разность — логарифму частного.
5.
1.loga a = 1 Логарифм по любому основанию a от самого этого основания равен единице.
2.loga 1 = 0 Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому что a0 = 1 — это прямое следствие из определения.
V.Решение примеров .
Давайте решим следующие примеры на доске..
Задание 1.
Какими формулами вы воспользуетесь при решении? (слайд 8)
log6 4 + log6 9.
log2 48 − log2 3.
log3 135 − log3 5.
4. Вычислить 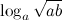 , если
, если 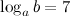
Привожу правильное решение примеров.
1.Найдите значение выражения: log6 4 + log6 9.
Решение
Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log6 4 + log6 9 = log6 (4 · 9) = log6 36 = 2.
Ответ:2
2.Найдите значение выражения: log2 48 − log2 3.
Решение
Основания одинаковые, используем формулу разности:
log2 48 − log2 3 = log2 (48 : 3) = log2 16 = 4.
Ответ:4
3.Найдите значение выражения: log3 135 − log3 5.
Решение
Основания одинаковые, поэтому имеем:
log3 135 − log3 5 = log3 (135 : 5) = log3 27 = 3.
Ответ:3
4. Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения:
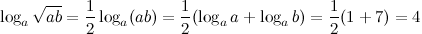
Ответ. 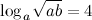
Задание 2.
Решите уравнения (1 и 2 уравнения решаются у доски, а 3,4,5,6 раздаются в виде карточек студентам (карточки разного уровня). (Решаем задания все на повторение. )
1)log3 (3х-7,5) = log3х
ОДЗ: x0;x2,5
Применяем потенцирование, получаем: x0;x.2,5
3х-7,5 = х
х=3,75
Ответ: х=3,75
2)log3 (6х-3) = 2
ОДЗ: x0,5
Исходя из определения логарифма, а именно, что логарифм - это число, в которое надо возвести основание, чтобы получить выражение, которое находится под знаком логарифма, т.е. (6х-3), получаем:
3 2 = 6х-3
6х-3 = 9
х =2
Ответ: х=2
3)Необходимо найти корень уравнения или сумму корней, если их несколько:
log3 (4х 2-12) = log3 (8х)
Применяем потенцирование, здесь оно допустимо. В итоге получаем обычное квадратное уравнение.
4х 2-12 = 8х
х 2-3 = 2х
х 2-2х-3 = 0
Находим корни уравнения:
х1= 3
х2= -1
Получилось два корня
Проверим результат и подставим его в исходное уравнение. Начнем с х1= 3:
log324 = log324
Проверка прошла успешно, теперь очередь х2= -1:
log3 (-8) = log3 (-8)- решений нет
Ответ 3.
Решение логарифмических нераванств.
Задание 3.
Пример 1. Решите неравенство 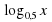
Решение. Пусть 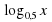 =
= 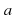 . Далее решим неравенство
. Далее решим неравенство 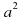
Получим:
(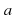 – 1)(
– 1)(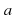 + 1) -1
+ 1) -1
Осталось решить двойное неравенство:
- 1 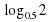
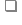 2 x 0,5.
2 x 0,5.
Ответ: 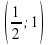 .
.
Пример 2. Решите неравенство 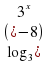 2
2 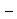 x.
x.
Решение. Перепишем неравенство в виде:
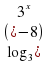
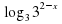
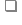
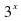
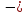 8
8 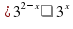
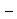 8
8 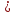
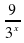 .
.
Пусть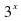
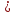
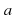 , получим:
, получим:
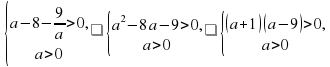
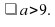
Осталось решить неравенство 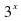
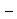 9.
9.
Ответ: (2; +∞).
Пример 3. Решите неравенство 2 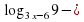
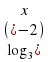 ≥ 1.
≥ 1.
Решение. Перепишем неравенство виде:
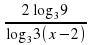 -
- 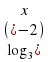 ≥ 1
≥ 1 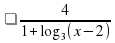 -
- 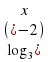 ≥ 1.
≥ 1.
Пусть a = 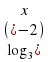 , тогда
, тогда
 – a ≥ 1
– a ≥ 1  ≥ 0
≥ 0 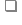
 ≥ 0
≥ 0 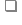
 ≤ 0.
≤ 0.
Далее воспользуемся методом интервалов. Получим: 
Осталось решить совокупность неравенств:
Ответ: 

 ;
;  .
.
Пример 4. Решите неравенство 
Решение. Последовательно воспользуемся утверждениями:

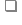


Двойное неравенство равносильно системе:
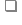


Ответ: (7; + ∞).
Пример 5. Решите неравенство 
Решение. Рассмотрим случаи:
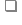
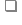
 2
2
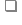
Но при x  неравенство 35 – x
неравенство 35 – x  неверно. Решений нет.
неверно. Решений нет.
Ответ: (2; 3).
VI. Самостоятельное применение знаний, умений и навыков.
Для достижения поставленной цели урока вам надо показать свои знания. На доске задания для самостоятельной работы по вариантам. Решаете задания на листочках.(3 варианта заданий на 5 минут) (слайд 9)
Iвариант.
II вариант.

Подробное решение примеров.
Iвариант.
Решите неравенство 
Решение.
Данное неравенство равносильно системе:


1) 

 ,
, .
.
2) 


Найдя общие решения неравенств 1) , 2) и учитывая, что  окончательно получим
окончательно получим
 Ответ:
Ответ: 
II вариант.
Решите неравенство 
Решение. Данное неравенство равносильно совокупности двух систем (метод расщепления неравенств):
Решим каждую систему совокупности.
1)
2) ø
Ответ: 
Передаём листочки с решениями преподавателю.
VII. Подведение итогов урока:
Сегодня на уроке мы закрепили навыки решения логарифмических неравенств, повторили правила вычисления логарифмов с помощью изученных свойств, рассмотрели вычисление десятичных логарифмов и решение логарифмических уравнений .
Выставление оценок за урок.
VIII. Домашнее задание:
§18 №18.4(а,б,в).(слайд 10)
Список литературы:
1. Выгодский М.Я. Справочник по элементарной математике. — М.: АСТ, 2003.
2. Алгебра и начала анализа: Учеб. для 10–11 кл. общеобразовательных учреждений / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; Под. ред. А.Н. Колмогорова. – М.: Просвещение, 2004.
3. 5. Алгебра и начала математического анализа. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных . учреждений (профильный уровень)/А.Г. Мордкович и др. ; под редакцией А.Г. Мордковича—2-е изд., стер.—М.: Мнемозина, 2014.
4. Алгебра и начала анализа: Учеб. для 10 кл. общеобразоват. учреждений /С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – М.: Просвещение, 2003.
5. Задачи по алгебре и началам анализа: Пособие для учащихся 10–11 кл. общеобразоват. учреждений /С.М. Саакян, А.М. Гольдман, Д.В. Денисов. – М.: Просвещение, 2003.
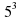 = 3
= 3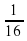 = –2
= –2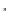 (-3)=; log
(-3)=; log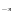 3=)
3=)  =8
=8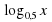
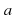 . Далее решим неравенство
. Далее решим неравенство 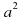
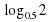
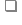 2
2 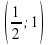 .
.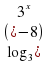 2
2 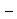
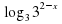
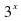
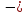 8
8 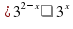
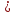
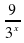 .
.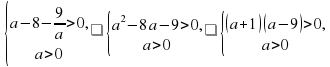
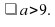
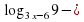
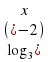 ≥ 1.
≥ 1.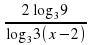 -
- 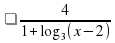 -
-