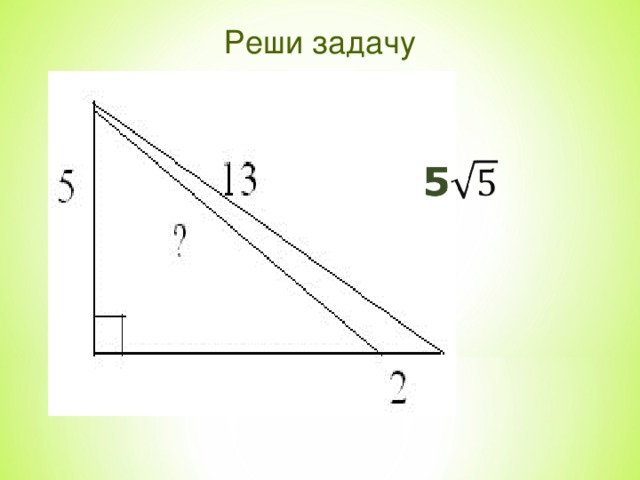
Методическая разработка урока геометрии по теме
"Теорема Пифагора", 8 класс.
Цель и задачи урока: изучить теорему Пифагора; рассмотреть решение задач с использованием этой теоремы; развивать у учащихся исследовательские способности.
“ Пифагор впервые разработал принципы геометрии,
исследовал теоремы невещественным, разумным путём.”
Прокл V в. Н. э.
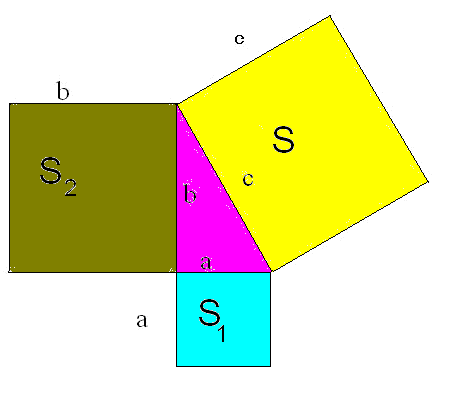
Оборудование: таблицы квадратов, чертёжные принадлежность, наборы для каждого ученика в конверте (прямоугольный треугольник, 3 квадрата, стороны которых соответственно равны гипотенузе и 2 катетам).
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Методическая разработка урока по теме "Теорема Пифагора"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Урок геометрии по теме Теорема Пифагора»
Просмотр содержимого презентации
«Приложение 1»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1970 руб.
2820 руб.
2020 руб.
2880 руб.
1670 руб.
2380 руб.
1570 руб.
2240 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
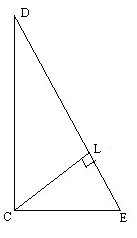 .
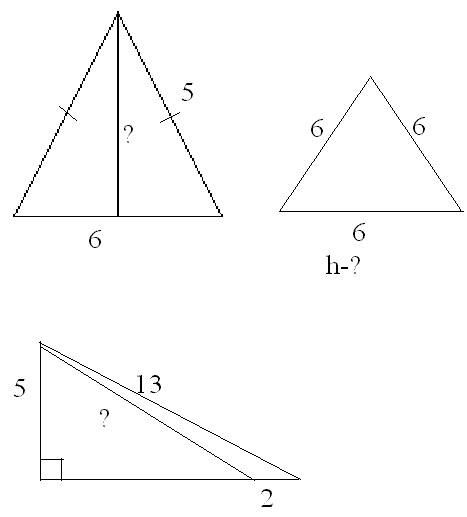
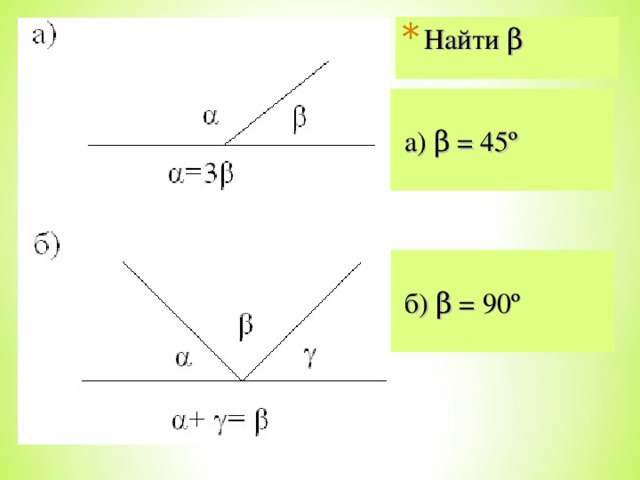
. 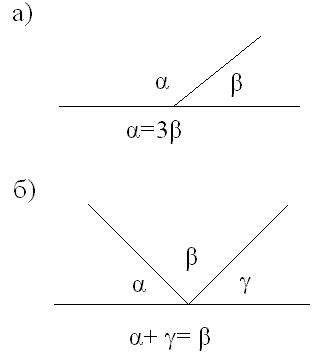 . Найдите
. Найдите