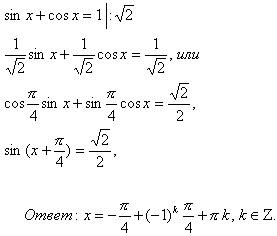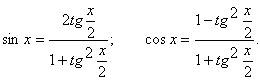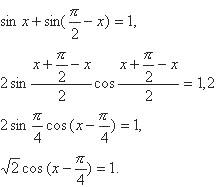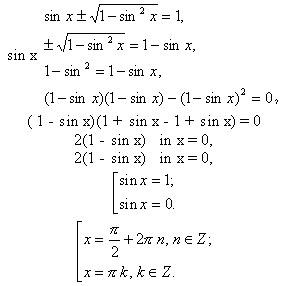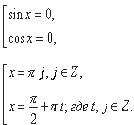1. Блошкин Б.Ф. «Самостоятельные и контрольные работы по математике 9-10 классы». М., Просвещение 1969 Богомолов И.В., Сергиенко Л.Ю. 2. «Сборник дидактических заданий по математике. М., Высшая школа, 1986
3. Зильберберг Н.И. «Алгебра и начала анализа в 10 классе» (для углубленного изучения математики) Псков, ПОИПКРО, 1994
4. Звавич Л.И., Шляпочник Л.Я. «Контрольные и проверочные работы по алгебре 10-11 классы» М., Дрофа, 2001
5. Ивлев Б.М. «Задачи повышенной трудности по алгебре и началам анализа». М., Просвещение, 1990
6. Ивлев Б.М., Саакян С.М., Шварцбурд С.И. «Дидактические материалы по алгебре и началам анализа. 10 класс». М., Просвещение, 1997
7. Кононов А.Я. «Устные занятия по математике в старших классах» М., Столетие, 1997
8. Краснова Л.Г., Матвеева Е.Д., Степанова М.И. «Сборник контрольных заданий» Чувашия, РИПКРНО, 1983
9. Самусенко А.В. «Математика: типичные ошибки абитуриентов» Минск, Высшая школа, 1995
10. Щукина В. «Репетитор. Математика. Физика» М., НПО Перспектива, 1993
11. http://www.falto.ru/article/article4_1.html
| Этапы урока | Цель | Содержание взаимодействия с учащимися | Методы и приемы работы | Ф И Г
| Деятельность учителя | Деятельность учащегося | Вывод |
| 1 этап: Организационный | Проверка готовноси обучающихся, их настроя на работу | Правильному применению методов можно научиться, только применяя их.. (Цейтен) |
| Ф | Приветствует обучающихся, проверяет их готовность к уроку | Приветствуют учителя, проверяют свою готовность к уроку |
|
| Выход на тему, цель, учебные задачи, устный счет | Подведение детей к формированию темы и постановке задач урока. Составление плана урока. | 1 задание. Устный счет – используя основные формулы тригонометрии, упростите выражение. На экране проецируется задание, затем появляются ответы А) (sin a – 1) (sin a + 1) Б) sin2 a – 1 + cos2 a В) sin2 a + tg a ctg a + cos2 a Г) √1- 2 tgх + tg2 х | Наблюдение, проблемная ситуация. Работа по плану урока | Ф | Организует диалог с обучающимися, в ходе которого повторяются основные формулы тригонометрии | Устно решают и объясняют почему получились такие ответы | Выявить, знают ли учащиеся основные тригонометрические формулы |
| 2 этап: Тестирование | Проверка понимания нахождения значений тригонометрических функций | Вариант 1. sin (-π/3); cos2π/3; tg π/6; ctg π/4; cos(-π/6); sin 3π/4 Вариант 2. cos(-π/4 ); sin π/3; ctg π/6 tg π/4; sin (-π/6); cos 5π/6 | Самостоятельная работа по вариантам, рефлексия, контроль | И, Ф | Проводит инструктаж обучающихся. Организует выступление обучающихся. | Выполняют задания на листках контроля с последующей самопроверкой | Выявить, умеют ли учащиеся находить значения тригонометрических функций |
| Тестирование | Проверка понимания нахождения значений обратных тригонометрических функций | Вариант 1. arcsin√2/2; arccos1; arcsin(-1/2); arccos(-√3/2); arctg√3 Вариант 2. arccos√2/2; arcsin1; arccos(-1/2) arcsin (-√3/2); arctg√3/3 | Самостоятельная работа по вариантам, рефлексия, контроль | И, Ф | Проводит инструктаж обучающихся. Организует выступление обучающихся. | Выполняют задания на листках контроля с последующей самопроверкой | Выявить, умеют ли учащиеся находить значения обратных тригонометрических функций |
| Устный счет | Проверка знаний формул решения простейших тригонометрических уравнений | На экране проецируется задание, затем появляются ответы sinx =а; cosx = а;tg х = а | Наблюдение, проблемная ситуация. Работа по плану урока | Ф | Организует диалог с обучающимися, в ходе которого повторяются формулы решения простейших тригонометрических уравнений | Устно решают и объясняют почему получились такие ответы | Выявить, знают ли учащиеся формулы решения простейших тригонометрических уравнений |
| Устный счет | Проверка знаний формул решения частных случаев простейших тригонометрических уравнений | На экране проецируется задание, затем появляются ответы sinx =0; cosx = 0; tg х = 0; sinx =1; cosx = 1; tg х = 1; sinx =-1; cosx = -1; | Наблюдение, проблемная ситуация. Работа по плану урока | Ф | Организует диалог с обучающимися, в ходе которого повторяются формулы решения частных случаев простейших тригонометрических уравнений | Устно решают и объясняют почему получились такие ответы | Выявить, знают ли учащиеся формулы решения частных случаев простейших тригонометрических уравнений |
| 3 этап урока: Решить уравнение sin x + cos x = 1 шестью различными методами. Класс разбивается на шесть команд. Каждая команда решает уравнение одним из предложенных методов, с последующей защитой своей работы у доски, указывая все его достоинства и недостатки | Решить уравнение с помощью введения вспомогательного угла с целью закрепления и повторения данного метода
| 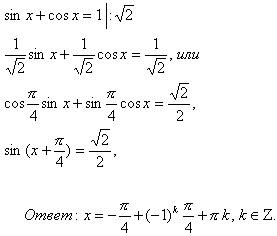
| Проблемная ситуация. | Ф, Г, И | Ставит перед учащимися задачу, определив способ решения | Именно этим способом решают данное уравнение, используя различные приёмы. |
|
| Решить уравнение с помощью введения универсальной тригонометрической подстановки с целью закрепления и повторения данного метода | 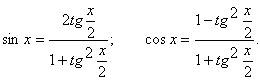
| Проблемная ситуация. | Ф, Г, И | Ставит перед учащимися задачу, определив способ решения | Именно этим способом решают данное уравнение, используя различные приёмы. | tgx / 2 не существует. Наличие или отсутствие решений x   +2 +2 n, n n, n  Z. может быть установлено проверкой Z. может быть установлено проверкой |
| Решить уравнение с помощью сведения к однородному уравнению с целью закрепления и повторения данного метода | Надо перейти к аргументу x/2 и применить формулы половинного аргумента к функциям в левой и правой частях уравнения sin x + cos x = 1. 2sinx/2*cosx/2 + cos 2 x/2- sin2x/2 = sin2x/2 + cos2x/2 | Проблемная ситуация. | Ф, Г, И | Ставит перед учащимися задачу, определив способ решения | Именно этим способом решают данное уравнение, используя различные приёмы. |
|
| Решить уравнение с помощью преобразования суммы в произведение с целью закрепления и повторения данного метода | Выразим cos x через sin( /2 – x): /2 – x): 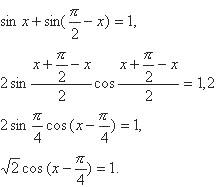
| Проблемная ситуация. | Ф, Г, И | Ставит перед учащимися задачу, определив способ решения | Именно этим способом решают данное уравнение, используя различные приёмы. |
|
| Решить уравнение с помощью замены cos x на 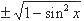 : с целью закрепления и повторения данного метода : с целью закрепления и повторения данного метода | 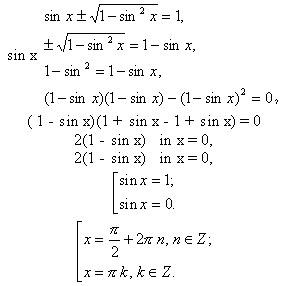
| Проблемная ситуация. | Ф, Г, И | Ставит перед учащимися задачу, определив способ решения | Именно этим способом решают данное уравнение, используя различные приёмы. | Решая этим методом нужно обязательно делать проверку. |
| Решить уравнение графически с целью закрепления и повторения данного метода |
| Проблемная ситуация. | Ф, Г, И | Ставит перед учащимися задачу, определив способ решения | Именно этим способом решают данное уравнение, используя различные приёмы. | Этим методом можно пользоваться не всегда |
| Решить уравнение с помощью возведения в квадрат обеих частей с целью закрепления и повторения данного метода | sin x + cos x = 1, (sin x + cos x) 2 = 1, 2 sin x cos x + 1= 1, 2 sin x cos x = 0, sin x cos x = 0, 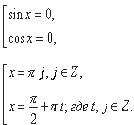
| Проблемная ситуация. | Ф, Г, И | Ставит перед учащимися задачу, определив способ решения | Именно этим способом решают данное уравнение, используя различные приёмы. | Этот метод нецелесообразен, т. к. проверка бывает затруднительной |
| 4 этап урока: Решить самостоятельно уравнение 5sin x – -12cos x = 13 тремя различными способами | Проверка целесообразности понимания и применения методов решения тригонометрических уравнений | Оценка «5» ставится за три правильно решенных способа, «4» за два способа, «3» за один способ. | Проблемная ситуация. | И | Ставит перед учащимися задачу, определив способ решения | решают данное уравнение, используя различные приёмы. |
|
| Подведение итогов | Соотнесение поставленных задач с достигнутым результатом |
| Рефлексия, контроль | Ф, Г, И | Задает вопросы о задачах урока | Проговаривают по плану новые знания, высказывают свои |
|
| Этап разъяснения домашнего задания | Обеспечение понимания учащимися цели, содержания и способов выполнения домашнего задания | Решить уравнение: 2sin x + 3cos x = 1. На «3» используя один из предложенных способов. На «4» используя два из предложенных способов. На «5» используя три из предложенных способов. | Повторить тригонометрические формулы | Ф, И | Проводит разбор и пояснение домашнего задания. | Записывают задания на дом, задают вопросы |
|
| Заключительный этап и рефлексия | Обеспечение позитивного настроения на получение знаний | Поставьте лодочку в том месте графического решения уравнения, которое отражает ваши ощущения на уроке: чувствовали ли вы себя на гребне волны или же, наоборот, тонули и были в самой нижней точке. | Рефлексия КОД (контрольно-оценочная деятельность) | Ф | Обеспечивает положительную реакцию учащихся на уроке математики | Получают позитивный настрой от урока | Одно и тоже уравнение можно решать различными методами |