| № этапа | Этапы занятия, учебные вопросы, формы и методы обучения | Временная регламентация этапа |
| 1 | Организационный этап: | 5 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – подготовить обучающихся к работе на уроке. СОДЕРЖАНИЕ – взаимные приветствия, фиксация отсутствующих, проверка внешнего состояния аудитории и готовности обучающихся к занятию, организация внимания. |
|
|
| - Сообщение правил заполнения листа самоанализа: | № | Вид работы | Баллы | | 1 | Устная работа(проверка домашнего задания) |
| | 2 | Письменная работа |
| | 3 | Работа в подгруппах(парах) |
| | 4 | Самостоятельная работа |
| | ИТОГО |
|
| Критерий оценивания: | Оценка | Баллы | | 5 | 12 и более | | 4 | 7-10 | | 3 | 3-6 | | 2 | 0-2 |
|
|
| 2. | Этап проверки домашнего задания | 15 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – установить правильность и осознанность выполнения домашнего задания всеми обучающимися, установить в ходе проверки обнаруженные пробелы в знаниях, совершенствую при этом знания, умения, навыки. |
|
|
| Содержание: фронтальный опрос, карточки с заданиями |
|
|
| 1) Ответить устно на следующие вопросы: Назовите свойства функций 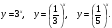 Как называются эти функции? Каковы общие свойства этих функций? Каковы их различные свойства? Существует ли наибольшее и наименьшее значения этих функций? Схематически изобразите графики функций 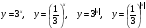 (если позволяет доска). (если позволяет доска). 2) Выясните, при каких значениях  имеет смысл выражение: имеет смысл выражение: 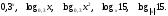
3) Найти  , если , если 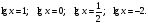
|
|
|
| | Количество правильных ответов | Баллы | | Менее 4 | 0 | | 5 | 1 | | 8 | 2 |
|
|
| 3 | Этап подготовки обучающихся к активному и сознательному усвоению материала | 10 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – организовать и направить на достижение цели познавательную деятельность обучающихся, постановка целей учебной деятельности. |
|
|
| «За всю историю человечества пока не найдено лучшего способа развития интеллектуальных и творческих способностей человека , чем при помощи математики» Владимир Тихомиров, профессор МГУ. |
|
|
| Сообщение темы, цели и задач материала; 2. 1) Закончите предложение: «Логарифм числа – это …» (десятичный логарифм – это). 2) «Логарифм частного равен …» 3) Записать формулу перехода от одного основания к другому. 4) Вычислить. а) 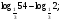 б) 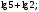 в) 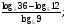 г) г) 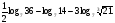 |
|
| 4 | Этап усвоения новых знаний | 15 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – дать обучающимся конкретное представление об изучаемых фактах, явлениях, основной идее изучаемого материала; добиться от обучающихся восприятия, осознания, первичного обобщения и систематизации новых знаний, усвоения обучающимися способов, путей, средств получения знаний, оперирования ими. |
|
|
| Содержание: |
|
|
| Дать определение логарифмической функции. Для обоснования основных свойств построить в одной системе координат графики функций 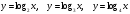 по точкам. Составим таблицы значений аргументов и соответствующих значений функций. по точкам. Составим таблицы значений аргументов и соответствующих значений функций. 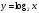
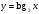 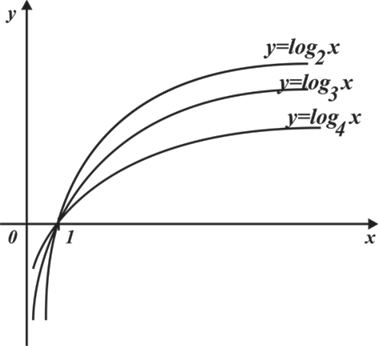
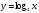
Используем этот рисунок для перечисления основных свойств логарифмической функции 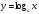 , при , при 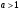 . . 1) 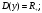 2) 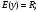 3) график проходит через точку (1; 0). 4)Наименьшего и наибольшего значений функция не имеет. 5) Функция не является ни нечетной, ни четной. Имеет общий вид. 6) Функция непериодическая. 7) Нули функции. График функции пересекает координатную ось Ox в точке (1; 0). 8) При a1 функция возрастает; при 0
|
|
| | ДИНАМИЧЕСКАЯ ПАУЗА | 5 |
|
| Далее предложить учащимся самостоятельно построить графики функций 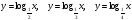 , то есть графики логарифмической функции при , то есть графики логарифмической функции при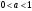 . Можно предложить подсказку в виде значений аргументов для исходных таблиц. . Можно предложить подсказку в виде значений аргументов для исходных таблиц. 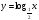
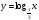
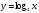
Учащиеся должны записать общие свойства для этих графиков функций. Утверждение о симметричности графиков показательной и логарифмической функций относительно прямой 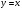 учитель демонстрирует по учебнику (стр. 239, рис. 136). учитель демонстрирует по учебнику (стр. 239, рис. 136). Задание из ЕГЭ. Задание 1А: Найдите область определения функции 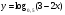 . . 1) 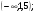 2) 2) 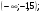 3) 3) 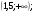 4) 4) 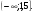 Ответ: 1. Задание 2А: Найдите область определения функции 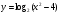 . . 1)  2) 2)  3) 3)  4) 4)  Ответ: 2. Задание 3А: Найдите область определения функции  . . 1)  2) 2)  3)  4) 4)  Ответ: 2. | 20 |
| 5 | Этап проверки понимания обучающимися материала | 5 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – установить осмыслили ли обучающиеся связи и отношения фактов, содержание новых понятий, закономерностей, устранить обнаруженные пробелы. |
|
|
| Используя записи в тетради и учебник, назвать основные вопросы и формулы по данной теме |
|
|
| Критерий оценивания: | Количество ошибок, допущенных при решении примеров | Баллы | | 1 | 2 | | 2 | 1 | | 3 и более | 0 |
|
|
| 6 | Этап закрепления нового материала | 10 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – закрепить у обучающихся знания и умения, необходимые для самостоятельной работы по новому материалу. |
|
|
| Решить №№ 499(а, б), 500(а, б), 505(а, б). Решить следующие задачи №№ 500(в, г), 505(в, г). Задание 1А: Найдите область определения функции  . . 1)  2) 2)  3) 3)  4) 4)  Ответ: 2. Задание 2А: Найдите область определения функции  . . 1)  2) 2)  3)  4) 4)  Ответ: 2. Задание 3А: Найдите область определения функции  . . 1)  2) 2)  3)  4) 4)  Ответ: 1. |
|
|
| Критерий оценивания учащихся отвечающих у доски: | Количество ошибок, допущенных при решении примеров | Баллы | | 1 | 2 | | 2 | 1 | | 3 и более | 0 |
Критерий оценивания учащихся решающих на месте: (выполнив задание, учащийся поднимает руку и показывает решение примера. В соответствии с критерием оценивания получает баллы за работу.) | Количество ошибок, допущенных при решении примеров | Баллы | | 1 | 3 | | 2 | 2 | | 3 | 1 | | 4 и более | 0 |
|
|
| 7 | Рефлексия учебной деятельности | 3 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – формирование у обучающихся умения анализировать результаты своей учебной деятельности. |
|
|
| обсуждение и оценка результатов самостоятельной работы (рефлексия в письменной форме) | Что нового Вы сегодня узнали? |
| | Своей работой на уроке Вы довольны? | Доволен /не доволен | | Ваше настроение после урока | Стало лучше / стало хуже | | Материал урока Вам был | Понятен / не понятен |
|
|
| 8 | Этап информации обучающихся о домашнем задании, инструктаж по его выполнению: | 7 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – подвести итоги и выставить оценки, сообщить обучающимся о домашнем задании, разъяснить методику его выполнения. |
|
|
|
|
|
|
|
|
|
|
| И если есть самостоятельная работа, то задания и форма контроля самостоятельной работы |
|
|
|
| 90 |
Преподаватель ___________________________________________________ Рахманина Э.М.
Укажите, какая из данных функций не является ни четной, ни нечетной.