МАОУ лицей №10 города Советска Калининградской области
учитель математики
Разыграева Татьяна Николаевна.
Конспект урока по алгебре в 11-м классе по теме:
«Логарифмическая функция, её свойства и график».
Тип урока: Открытие нового знания.
Цели урока: Ввести определение логарифмической функции. Формировать умение строить график логарифмической функции. Научить выявлять свойства логарифмической функции по графику.
Задачи урока:
Образовательная: повторить определение логарифма, план исследования свойств функции, вспомнить график и свойства показательной функции; сформировать умение строить график логарифмической функции, изучит свойства логарифмической функции;
осуществить контроль знаний с помощью проверочного задания и теста.
Развивающая: способствовать развитию внимания, развитию логического мышления, математической интуиции, умению анализировать, применять знания в нестандартных ситуациях,
Воспитательная: воспитывать информационную культуру, выработать навыки работы в группе и индивидуально.
Этапы урока:
1. Организационный момент
Учитель приветствует учащихся и рассказывает о цели урока.
Учитель: Мы с Вами продолжаем изучение 7 – ой главы. Сегодня познакомимся с новой функцией – логарифмической, построим её график и изучим свойства.
2. Актуализация познавательного интереса к изучаемой теме
Учитель предлагает решить учащимся задания устной разминки. Называя координаты ячейки и открывая её, считаем логарифмы. В некоторых ячейках есть буквы. После решения всех заданий из этих букв выстраивается фамилия Непер – математик, изобретатель логарифмов (слайд 2,3).
На слайде показывается его портрет и краткая справка о нём.
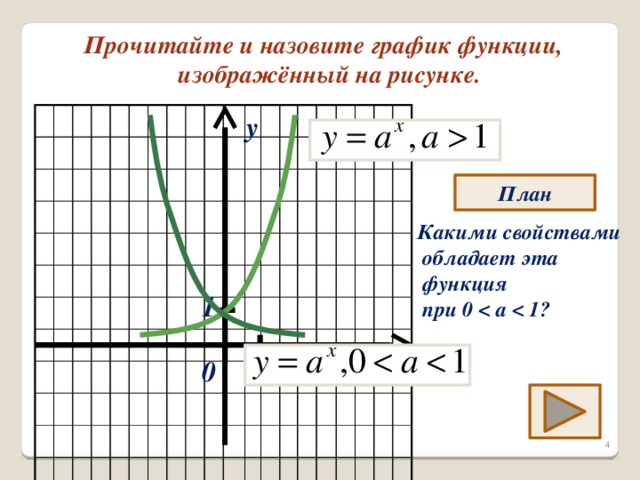
Вторая часть устной разминки – прочитать и назвать график функции, изображённый на рисунке. Можно воспользоваться подсказкой – «План» или проверить, все ли свойства отражены в ответе. Ученики узнают на рисунке график показательной функции при a 1. Далее учащимся надо ответить на вопрос: какими свойствами обладает эта функция при 0 ? (сдайд4).
На следующем слайде появляется портрет великого математика – Леонарда Эйлера и краткая справка о нём. Учитель задаёт вопрос: Как вы думаете в связи с чем появился портрет этого учёного? Учитель выслушивает варианты ответов и, или подтверждает правильный ответ, или сообщает, что определение логарифмической функции – это заслуга Леонарда Эйлера. Итак, мы сегодня будем изучать логарифмическую функцию (слайд 6).
3. Актуализация темы урока, создание проблемной ситуации.
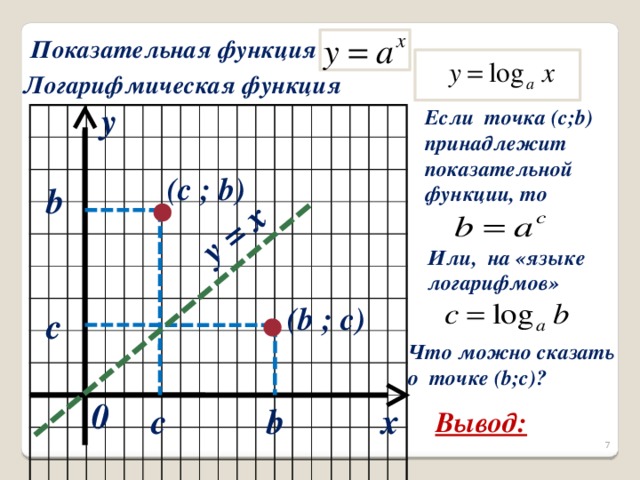
Учитель просит дать определение показательной функции и самостоятельно сформулировать определение логарифмической функции. В координатной плоскости построить точку с координатами (b;c) и, предположить, что она принадлежит графику показательной функции. Значит 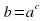 . Попробуйте переписать эту запись на «языке логарифмов». Т.е.
. Попробуйте переписать эту запись на «языке логарифмов». Т.е. 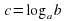 . Что можно сказать про точку с координатами (b;c)? Ответ: они симметричны относительно прямой у = х (слайд 7).
. Что можно сказать про точку с координатами (b;c)? Ответ: они симметричны относительно прямой у = х (слайд 7).
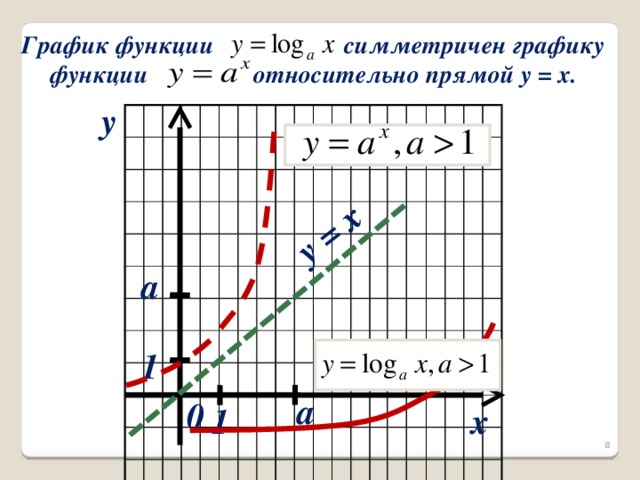
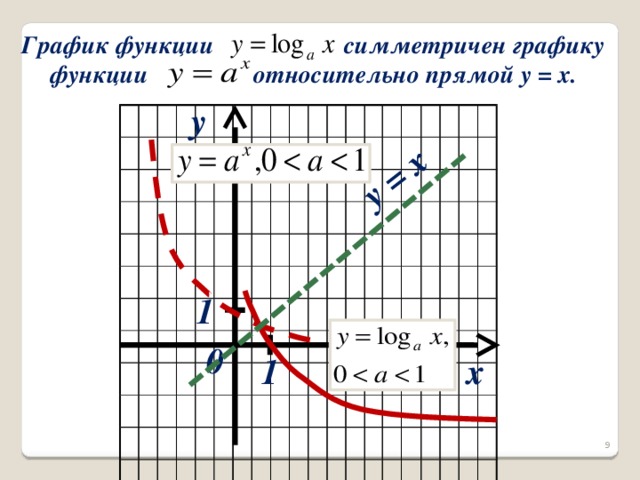
Сделайте вывод: график логарифмической функции симметричен графику показательной функции относительно прямой у = х. Учащимся предлагается сделать эскизы графиков при a 1(1 вариант) и при 0 (2 вариант). Правильность эскизов проверяется с помощью слайдов 8,9.
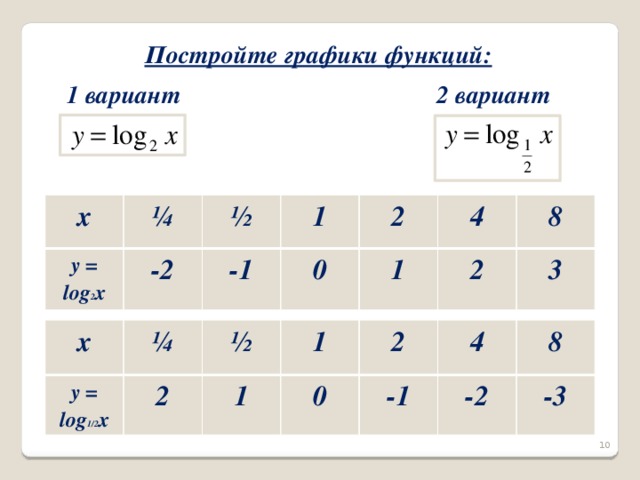
После проверки, учитель даёт задание: построить графики функций 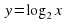 (1 вариант) и
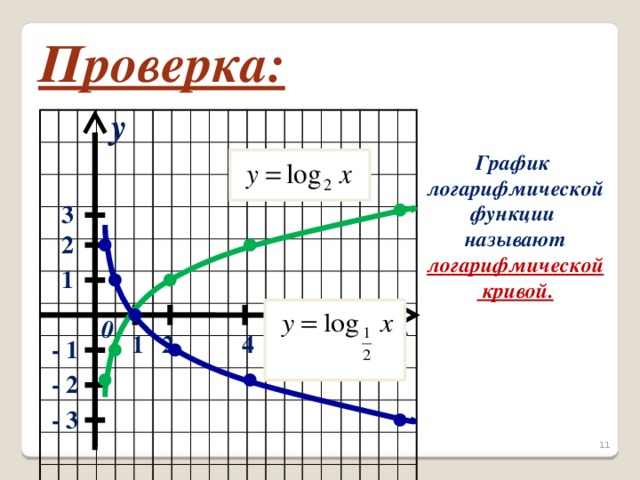
(1 вариант) и 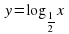 (2вариант). Правильность табличных результатов и графиков проверяется с помощью слайдов 10,11.
(2вариант). Правильность табличных результатов и графиков проверяется с помощью слайдов 10,11.
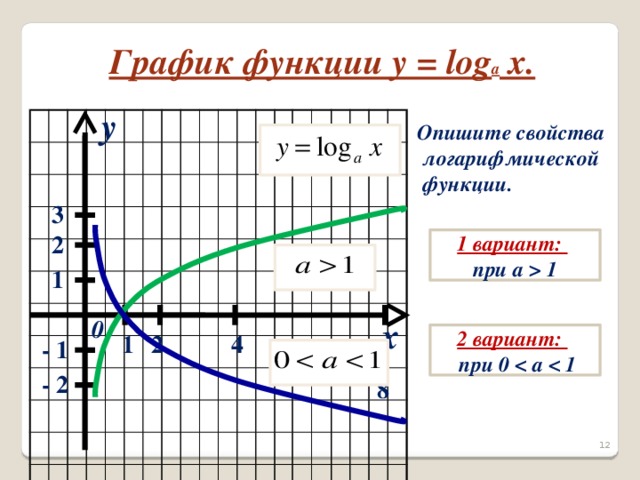
Учащимся предлагается сделать эскиз графика функции 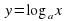 и описать его свойства при a 1(1 вариант) и при 0 (2 вариант). Проверка – слайд 13,14.
и описать его свойства при a 1(1 вариант) и при 0 (2 вариант). Проверка – слайд 13,14.
После проверки свойств графиков функций, учитель просит учащихся сделать вывод о свойствах логарифмической функции (слайд 15).
4. Динамическая пауза или разрядка для глаз.
(исходное положение - сидя, каждое упражнение повторяется 3-4 раза):
1. Откинувшись назад, сделать глубокий вдох, затем, наклонившись вперед, выдох.
2. Откинувшись на спинку стула, прикрыть веки, крепко зажмурить глаза, не открывая век.
3. Руки вдоль туловища, круговые движения плечами назад и вперёд.
4. Гимнастика для глаз с помощью тренажёра.
5. Закрепление изученного материала.
Учитель демонстрирует задания на слайдах презентации. Учащиеся устно решают первое задание.
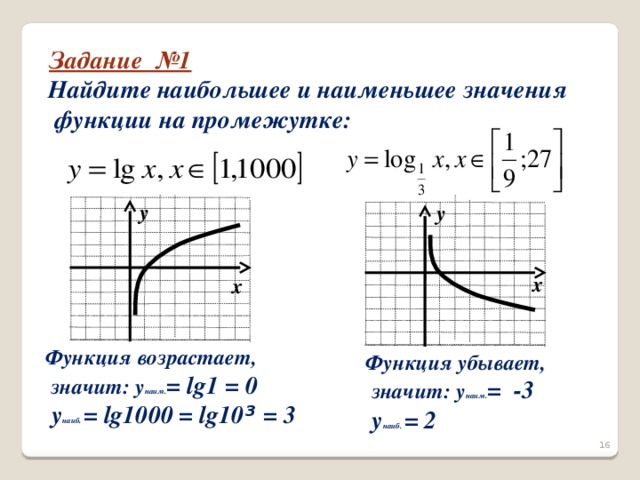
Задание 1. Найдите наименьшее и наибольшее значения функций на данном промежутке: а) 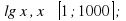 б)
б) 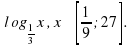
Правильность ответа проверяется с помощью презентации (слайд 16).
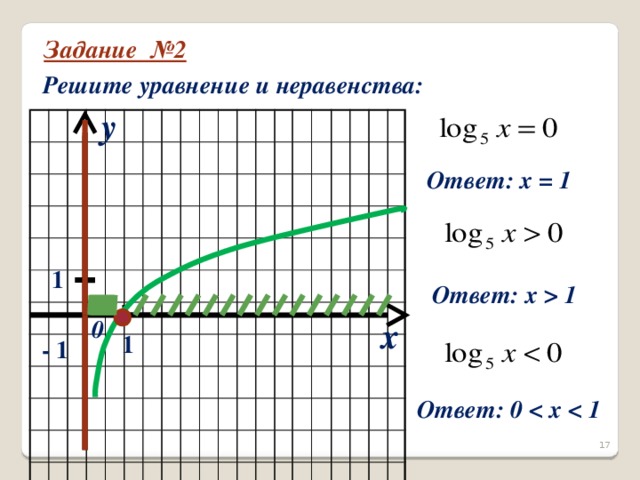
Аналогично решается второе задание (слайд 17).
Задание 2. Решите уравнения и неравенства: а) 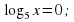
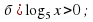
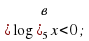
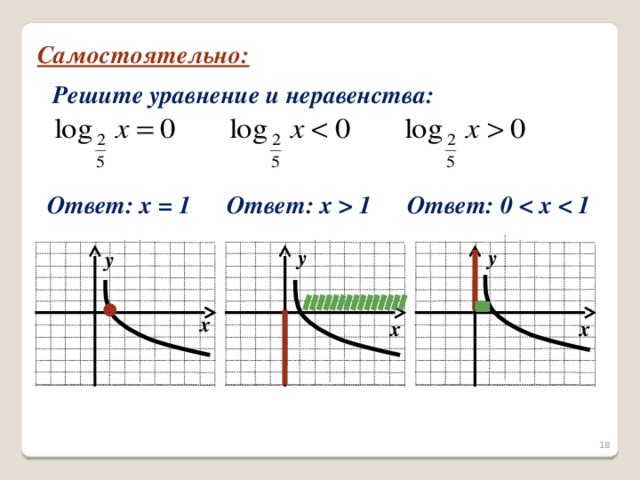
Похожее задание решаю самостоятельно, записывая только ответы в тетрадь (слайд 18).
Решите уравнения и неравенства: а) 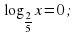
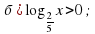
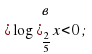
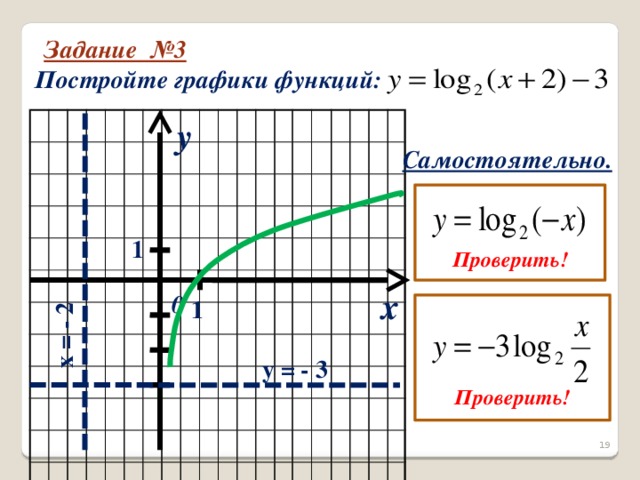
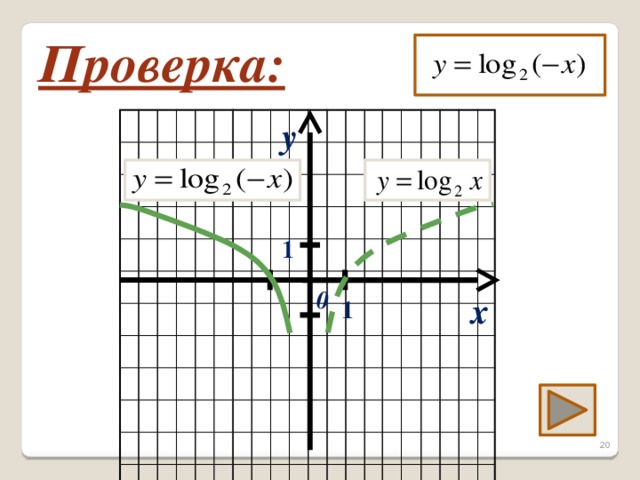
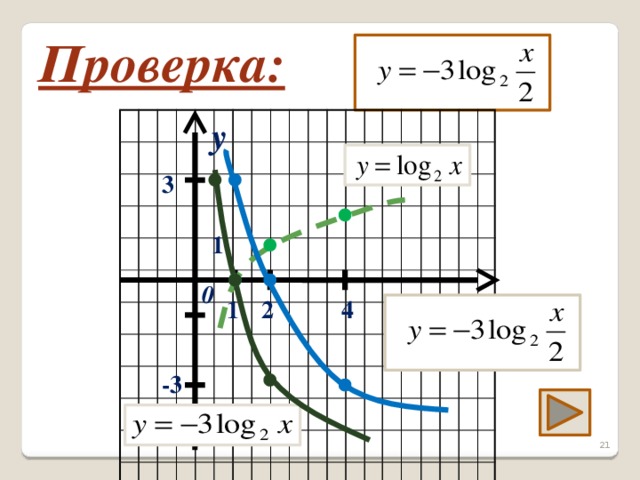
Третье задание на построение графика функции разбирает весь класс с помощью учителя. Далее самостоятельно строят графики функций в тетради с последующей проверкой (слайды 19 - 21).
Задание 3. Постройте графики функций: 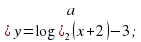
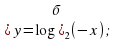
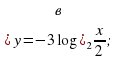
6. Подведение итогов и результатов работы на уроке (рефлексия).
Учитель предлагает учащимся блиц - опрос, чтобы проверить себя, на сколько каждый понял изученный материал (слайд 22 – 24). Необходимо ответить только «да» или «нет». Проверяется сразу.
Вопросы:
Ось у является вертикальной асимптотой графика логарифмической функции.
Графики показательной и логарифмической функций симметричны относительно прямой у = х.
Область определения логарифмической функции – вся числовая прямая, а область значений этой функции – промежуток 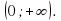
Монотонность логарифмической функции зависит от основания логарифма.
Не каждый график логарифмической функции проходит через точку с координатами (1; 0).
Логарифмическая кривая это та же экспонента, только по-другому расположенная в координатной плоскости.
Выпуклость логарифмической функции не зависит от основания логарифма.
Логарифмическая функция не является ни чётной, ни нечётной.
Логарифмическая функция имеет наибольшее значение и не имеет наименьшего значения при а 1 и наоборот при 0 a .
Проверка: да, да, нет, да, нет, да, нет, да, нет.
Учитель задаёт вопрос: Каковы результаты? Есть ли учащиеся, которые на все вопросы ответили правильно? У кого только одна или две ошибки? Если есть ученики, у которых больше четырёх ошибок, то не стоит отчаиваться, потому что есть возможность ещё раз дома просмотреть этот материал и найти правильные ответы на вопросы теста.
Учитель выводит на экран домашнее задание, делает соответствующие пояснения о том, какие результаты по его выполнению будут необходимы на следующем уроке. Учащиеся записывают задание.
Домашнее задание: § 49, № 1460, 1463, 1467, 1480 по вариантам. Первый вариант выполняет все номера под буквами а), б), а второй вариант под буквами в), г).
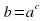 . Попробуйте переписать эту запись на «языке логарифмов». Т.е.
. Попробуйте переписать эту запись на «языке логарифмов». Т.е. 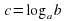 . Что можно сказать про точку с координатами (b;c)? Ответ: они симметричны относительно прямой у = х (слайд 7).
. Что можно сказать про точку с координатами (b;c)? Ответ: они симметричны относительно прямой у = х (слайд 7).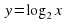 (1 вариант) и
(1 вариант) и 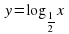 (2вариант). Правильность табличных результатов и графиков проверяется с помощью слайдов 10,11.
(2вариант). Правильность табличных результатов и графиков проверяется с помощью слайдов 10,11. 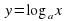 и описать его свойства при a 1(1 вариант) и при 0 (2 вариант). Проверка – слайд 13,14.
и описать его свойства при a 1(1 вариант) и при 0 (2 вариант). Проверка – слайд 13,14.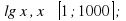 б)
б) 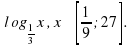
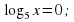
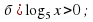
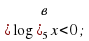
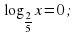
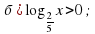
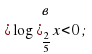
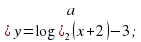
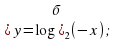
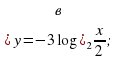
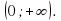





 1 1 0 x 2 1 4 2 вариант: при 0 - 1 - 2 8" width="640"
1 1 0 x 2 1 4 2 вариант: при 0 - 1 - 2 8" width="640"
 1. у 1) D(f) = (0, + ∞) ; 2) не является ни чётной, ни нечётной; х 0 3) возрастает на (0, + ∞) ; 4)не ограничена сверху, не ограничена снизу; 5)не имеет ни наибольшего, ни наименьшего значений; 6) непрерывна; 7) E(f) = (- ∞ , + ∞) ; 8) выпукла вверх. 13" width="640"
1. у 1) D(f) = (0, + ∞) ; 2) не является ни чётной, ни нечётной; х 0 3) возрастает на (0, + ∞) ; 4)не ограничена сверху, не ограничена снизу; 5)не имеет ни наибольшего, ни наименьшего значений; 6) непрерывна; 7) E(f) = (- ∞ , + ∞) ; 8) выпукла вверх. 13" width="640"

 1 1 0 D(f) = (0, + ∞) 2 не является ни чётной, ни нечётной; 3 возрастает на (0, + ∞) 4 не ограничена сверху, не ограничена снизу убывает на (0, + ∞) 5 не имеет ни наибольшего, ни наименьшего значений 6 непрерывна 7 E(f) = (- ∞ , + ∞) 8 выпукла вверх выпукла вниз" width="640"
1 1 0 D(f) = (0, + ∞) 2 не является ни чётной, ни нечётной; 3 возрастает на (0, + ∞) 4 не ограничена сверху, не ограничена снизу убывает на (0, + ∞) 5 не имеет ни наибольшего, ни наименьшего значений 6 непрерывна 7 E(f) = (- ∞ , + ∞) 8 выпукла вверх выпукла вниз" width="640"
 1 0 x 1 - 1 Ответ: 0" width="640"
1 0 x 1 - 1 Ответ: 0" width="640"
 1 Ответ: х = 1 у у у х х х 18" width="640"
1 Ответ: х = 1 у у у х х х 18" width="640"
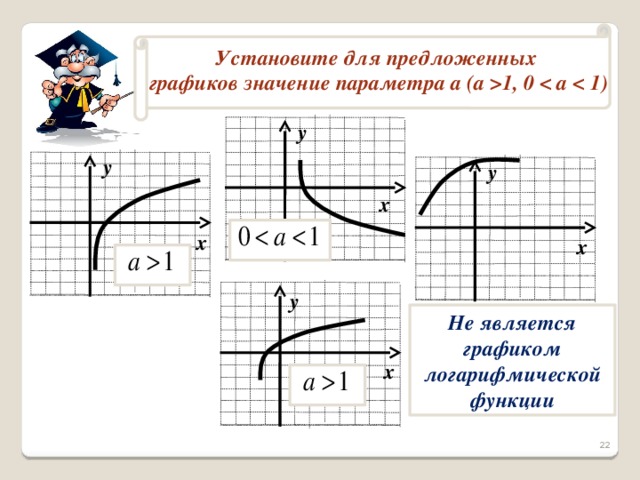 1, 0 у у у х х х у Не является графиком логарифмической функции х 22" width="640"
1, 0 у у у х х х у Не является графиком логарифмической функции х 22" width="640"

 1 и наоборот при 0 Проверка: Да, да, нет, да, нет, да, нет, да, нет 24" width="640"
1 и наоборот при 0 Проверка: Да, да, нет, да, нет, да, нет, да, нет 24" width="640"


















