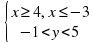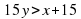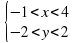Тема «Линейные уравнения, неравенства и системы неравенств с двумя переменными»
Тип урока: изучение нового материала.
Цели урока
Научить учащихся изображать на координатной плоскости множество решений
неравенств и систем линейных неравенств с двумя переменными.
Развивать коммуникативные навыки общения; умения слушать и слышать;
графическую культуру и математическую речь.
Воспитывать внимание, самоконтроль, интерес к предмету, настойчивость в
достижении цели.
Оборудование: инструменты для черчения.
План урока
| п/п | Этапы урока | Приемы и метод |
| 1 | Актуализация новых знаний. Мотивация изучения данной темы | Беседа учителя |
| 2 | Объяснение нового материала | Учитель объясняет новый материал |
| 3 | Первичное закрепление | Работа учащихся на местах и у доски |
| 4 | Рефлексия. Домашнее задание | Подведение итогов |
Этап №1
До сих пор мы с вами решали самые разнообразные уравнения и неравенства с одной переменной. Однако на языке неравенств ( и не обязательно с одной переменной) нередко формулируются задачи во многих приложениях математики ( учащиеся записывают число и тему урока ).
Давайте внимательно посмотрим на тему урока и попытаемся сформулировать те задачи, которые мы будем ставить перед собой при ее изучении (учащиеся формулируют задачи).
Дать определение таким понятиям как линейное уравнение, неравенство с двумя
переменными.
Что значит решить уравнение, неравенство.
Способы решения.
Что является решением уравнения, неравенства, системы неравенств с двумя
Переменными.
Вопрос учителя: «А какие способы решения мы знаем?» (алгебраический и графический).
Итак, сегодня мы с вами будем учиться решать линейные уравнения, неравенства, системы неравенств с двумя неизвестными.
Этап№2
Линейные уравнения с двумя переменными.
Начнем с определения. Уравнение вида  (1), где А,В,С – некоторые числа, х и у – переменные называется линейным уравнением с двумя переменными. Приведите примеры такого уравнения (ученики приводят свои примеры). Так как мы будем использовать графический способ, то нужно знать, а что будет являться графиком этого уравнения. Рассмотрим уравнение (1), где хотя бы одно из чисел А или В не равно нулю. Пусть В не равно нулю. Попытаемся выразить переменную у из уравнения (один ребенок комментирует с места свое решение учитель записывает его на доске все остальные пишут в тетрадях и если есть ошибки, то поправляют). В результате появляется запись
(1), где А,В,С – некоторые числа, х и у – переменные называется линейным уравнением с двумя переменными. Приведите примеры такого уравнения (ученики приводят свои примеры). Так как мы будем использовать графический способ, то нужно знать, а что будет являться графиком этого уравнения. Рассмотрим уравнение (1), где хотя бы одно из чисел А или В не равно нулю. Пусть В не равно нулю. Попытаемся выразить переменную у из уравнения (один ребенок комментирует с места свое решение учитель записывает его на доске все остальные пишут в тетрадях и если есть ошибки, то поправляют). В результате появляется запись 
Вопросы учителя. Чем являются выражения  и
и 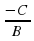 ? (в случае затруднения обратить внимание на определение). Значит их можно переобозначить, например,
? (в случае затруднения обратить внимание на определение). Значит их можно переобозначить, например, 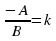 ;
; 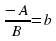 .
.
Какой вид примет уравнение (1)? 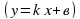 . А это что за функция и что является ее графиком? Учитель выслушивает ответы учащихся и подводит итог. Таким образом графиком уравнения (1) является прямая. Но какое ограничение накладывалось на число В?
. А это что за функция и что является ее графиком? Учитель выслушивает ответы учащихся и подводит итог. Таким образом графиком уравнения (1) является прямая. Но какое ограничение накладывалось на число В?  Какой вопрос возникает? (если
Какой вопрос возникает? (если  , то уравнение (1) примет вид
, то уравнение (1) примет вид 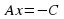 ,
,  т.е. число). Ученики вспоминают что является графиком такого уравнения и строят в тетрадях график уравнения
т.е. число). Ученики вспоминают что является графиком такого уравнения и строят в тетрадях график уравнения 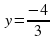 . Рассмотрим следующее уравнение:
. Рассмотрим следующее уравнение: 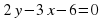 и пары чисел (0;3) и (1:3). Подставим эти пары чисел в наше уравнение (один ученик комментирует решение с места, учитель записывает на доске все остальные пишут в тетрадях и при необходимости поправляют). После этого учащиеся формулируют определение решения уравнения и сроят график данного уравнения (ученик у доски остальные в тетрадях).
и пары чисел (0;3) и (1:3). Подставим эти пары чисел в наше уравнение (один ученик комментирует решение с места, учитель записывает на доске все остальные пишут в тетрадях и при необходимости поправляют). После этого учащиеся формулируют определение решения уравнения и сроят график данного уравнения (ученик у доски остальные в тетрадях).
Линейные неравенства с двумя переменными.
Как вы считаете, чем будут отличаться определение линейного уравнения от определения линейного неравенства? Ученики отвечают и на доске и в тетрадях появляется запись 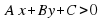 (2) или
(2) или 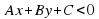 (3) или
(3) или 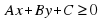 (4) или
(4) или 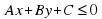 (5)
(5)
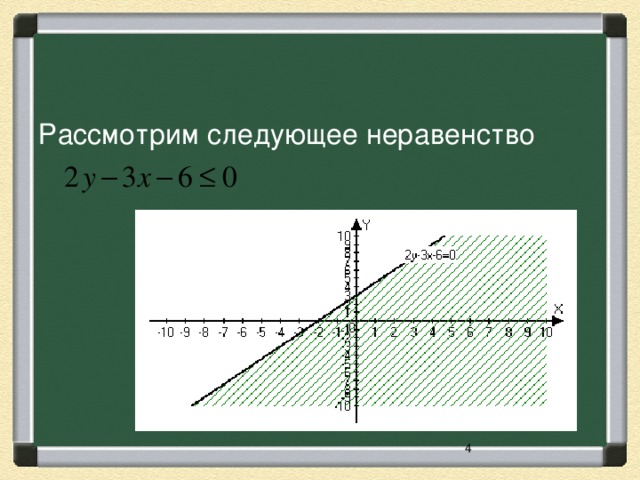
Рассмотрим следующее неравенство 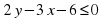 . Выясним, что будет являться решением этого неравенства. Что делает любая прямая с координатной плоскостью? (делит на две полуплоскости). Что является графиком уравнения
. Выясним, что будет являться решением этого неравенства. Что делает любая прямая с координатной плоскостью? (делит на две полуплоскости). Что является графиком уравнения 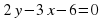 ? (прямая). Мы ее уже построили. По отношению к прямой, где лежат эти полуплоскости? (выше прямой и ниже). Давайте выберем произвольно точку из верхней полуплоскости и из нижней и подставим их координаты в наше неравенство (ученик работает у доски остальные в тетрадях).
? (прямая). Мы ее уже построили. По отношению к прямой, где лежат эти полуплоскости? (выше прямой и ниже). Давайте выберем произвольно точку из верхней полуплоскости и из нижней и подставим их координаты в наше неравенство (ученик работает у доски остальные в тетрадях).
Например, (0;0) и (0;4). В результате работы составляется алгоритм решения неравенства.
Самостоятельно в тетрадях выполняется задание: изобразить на координатной плоскости решение неравенства 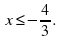
Если учащиеся не задали вопроса, то можно сделать замечание: А если неравенство строгое? Что изменится? После обсуждения ученики придут к выводу, что точки, лежащие на прямой не входят в решение и в этом случае прямая должна изображаться пунктиром.
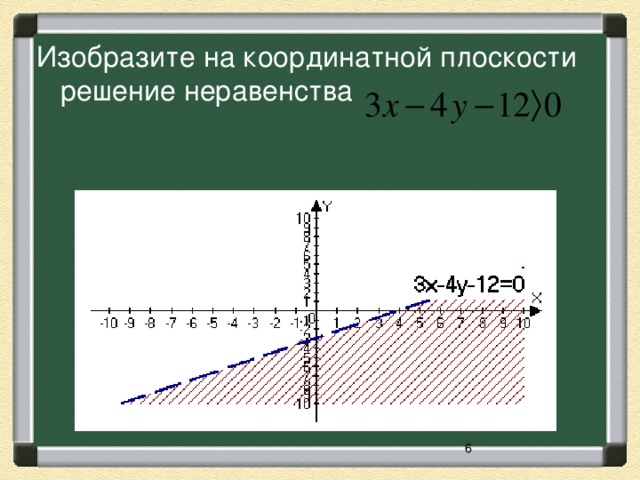
Изобразить на координатной плоскости решение неравенства  (ученик работает у доски остальные в тетрадях).
(ученик работает у доски остальные в тетрадях).
Системы неравенств.
Перейдем к системам неравенств с двумя переменными. Попробуйте дать определение системы неравенств с двумя переменными, опираясь на определение неравенства с двумя переменными. Дети формулируют определение при необходимости другие или учитель корректируют. (6) 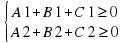

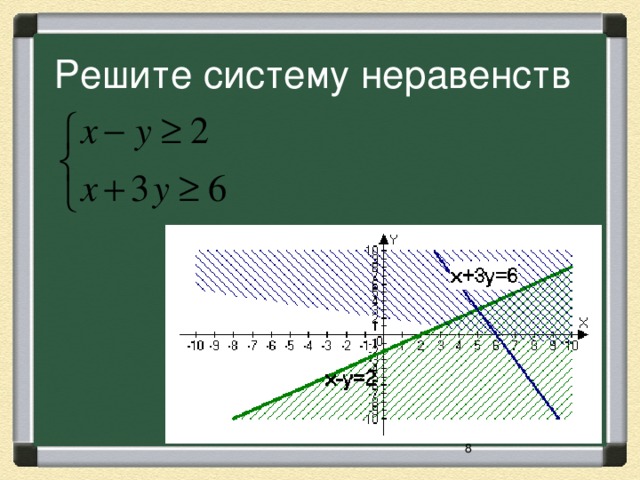
Как мы будем искать решение системы, опираясь на решение неравенства? После обсуждения дети формулируют алгоритм. Если первому неравенству системы (6) удовлетворяют точки множества М1, лежащие по одну сторону от прямой L1, а второму точки множества М2 прямой L2, то решением системы представляет собой пересечение множеств М1 и М2. Решить систему неравенств 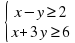
Работают два ученика по очереди. Один сроит границы, другой находит решение. Остальные в тетрадях.
Этап №3 Закрепление
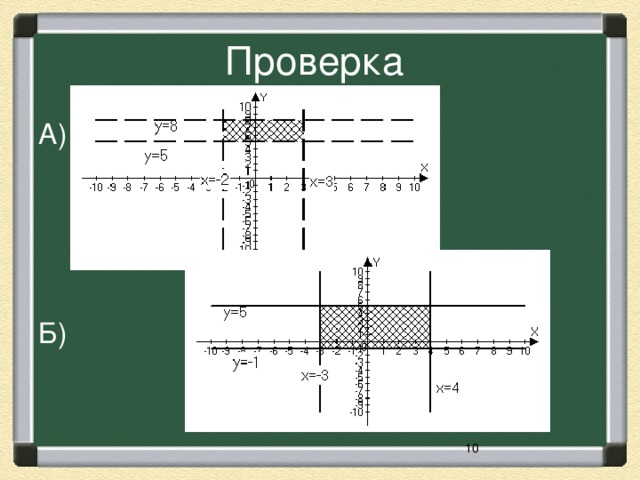
Решить систему неравенств графическим способом:
а)  б)
б) 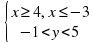
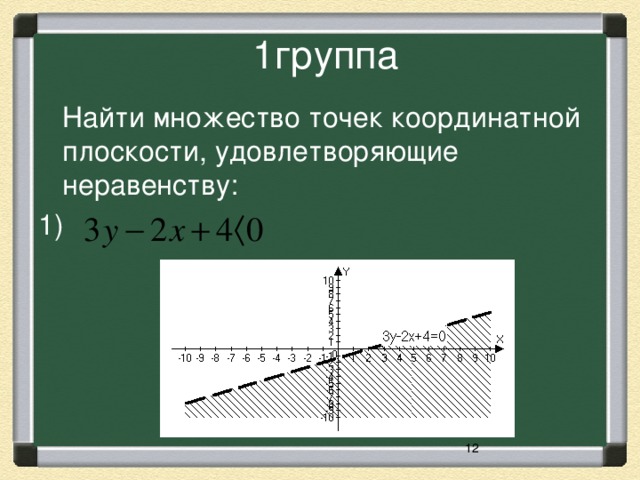
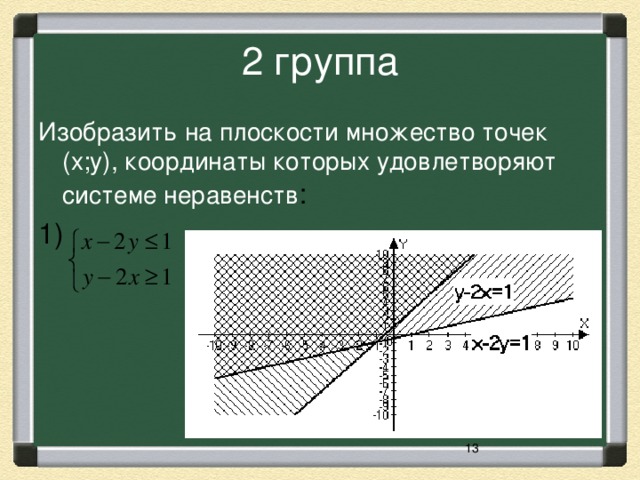
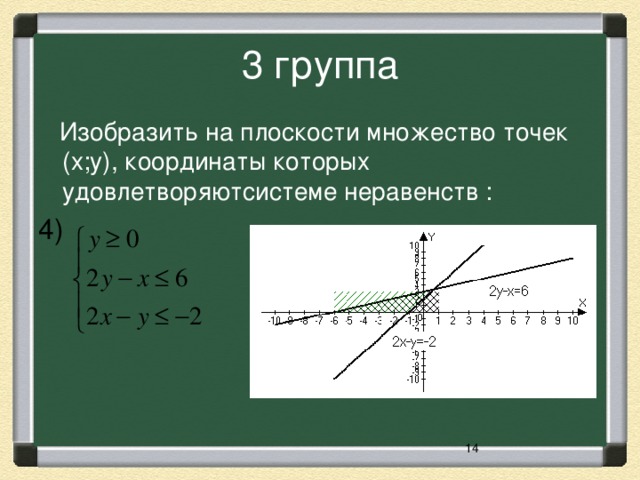
Разноуровневая работа по группам. Задания взяты из учебника Ю.М. Колягин «Алгебра и начала математического анализа 11 класс» (стр243).
| 1 группа | 2 группа | 3 группа |
| № 2(1) | № 3(1) | № 3(4) |
Проверка заданий с помощью мультимедиа. Выставление и комментирование оценок.
Этап №4. Рефлексия. Домашняя работа.
Итак, подведем итог.
Что является решением линейного уравнения с двумя переменными?
Что является решением линейного неравенства с двумя переменными?
Как определить какая из полуплоскостей будет являться решением?
Как найти решение системы неравенств?
Поднимите руку кому не понятно как находится решение уравнения, неравенства, системы неравенств?
Домашнее задание по группам. Теория стр. 237-240.
| 1 группа | 2 группа | 3 группа |
| № 2(2), 3(3) | № 3(2), 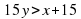 | № 3(3), 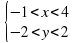 |
Творческое задание. Найти задачи прикладного характера, приводящие к решению систем неравенств.
 (1), где А,В,С – некоторые числа, х и у – переменные называется линейным уравнением с двумя переменными. Приведите примеры такого уравнения (ученики приводят свои примеры). Так как мы будем использовать графический способ, то нужно знать, а что будет являться графиком этого уравнения. Рассмотрим уравнение (1), где хотя бы одно из чисел А или В не равно нулю. Пусть В не равно нулю. Попытаемся выразить переменную у из уравнения (один ребенок комментирует с места свое решение учитель записывает его на доске все остальные пишут в тетрадях и если есть ошибки, то поправляют). В результате появляется запись
(1), где А,В,С – некоторые числа, х и у – переменные называется линейным уравнением с двумя переменными. Приведите примеры такого уравнения (ученики приводят свои примеры). Так как мы будем использовать графический способ, то нужно знать, а что будет являться графиком этого уравнения. Рассмотрим уравнение (1), где хотя бы одно из чисел А или В не равно нулю. Пусть В не равно нулю. Попытаемся выразить переменную у из уравнения (один ребенок комментирует с места свое решение учитель записывает его на доске все остальные пишут в тетрадях и если есть ошибки, то поправляют). В результате появляется запись 
 и
и 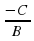 ? (в случае затруднения обратить внимание на определение). Значит их можно переобозначить, например,
? (в случае затруднения обратить внимание на определение). Значит их можно переобозначить, например, 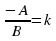 ;
; 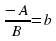 .
.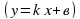 . А это что за функция и что является ее графиком? Учитель выслушивает ответы учащихся и подводит итог. Таким образом графиком уравнения (1) является прямая. Но какое ограничение накладывалось на число В?
. А это что за функция и что является ее графиком? Учитель выслушивает ответы учащихся и подводит итог. Таким образом графиком уравнения (1) является прямая. Но какое ограничение накладывалось на число В?  Какой вопрос возникает? (если
Какой вопрос возникает? (если  , то уравнение (1) примет вид
, то уравнение (1) примет вид 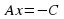 ,
,  т.е. число). Ученики вспоминают что является графиком такого уравнения и строят в тетрадях график уравнения
т.е. число). Ученики вспоминают что является графиком такого уравнения и строят в тетрадях график уравнения 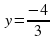 . Рассмотрим следующее уравнение:
. Рассмотрим следующее уравнение: 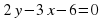 и пары чисел (0;3) и (1:3). Подставим эти пары чисел в наше уравнение (один ученик комментирует решение с места, учитель записывает на доске все остальные пишут в тетрадях и при необходимости поправляют). После этого учащиеся формулируют определение решения уравнения и сроят график данного уравнения (ученик у доски остальные в тетрадях).
и пары чисел (0;3) и (1:3). Подставим эти пары чисел в наше уравнение (один ученик комментирует решение с места, учитель записывает на доске все остальные пишут в тетрадях и при необходимости поправляют). После этого учащиеся формулируют определение решения уравнения и сроят график данного уравнения (ученик у доски остальные в тетрадях).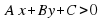 (2) или
(2) или 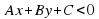 (3) или
(3) или 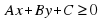 (4) или
(4) или 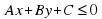 (5)
(5)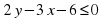 . Выясним, что будет являться решением этого неравенства. Что делает любая прямая с координатной плоскостью? (делит на две полуплоскости). Что является графиком уравнения
. Выясним, что будет являться решением этого неравенства. Что делает любая прямая с координатной плоскостью? (делит на две полуплоскости). Что является графиком уравнения 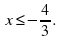
 (ученик работает у доски остальные в тетрадях).
(ученик работает у доски остальные в тетрадях).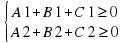

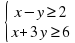
 б)
б)