Данный урок ориентирован на обучающихся 7 класса с углубленным изучением математики по учебнику «Алгебра 7», авторы Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е.Феоктистов. Урок проходит по сценарию мультимедийной презентации, что позволяет сэкономить время, которое тратит учитель на выполнение построения на доске. Презентация выполнена с помощью красочных иллюстраций и анимации. При необходимости этап урока, где возникли трудности, можно повторить. На уроке использованы материалы, не входящие в обязательные стандарты образования.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
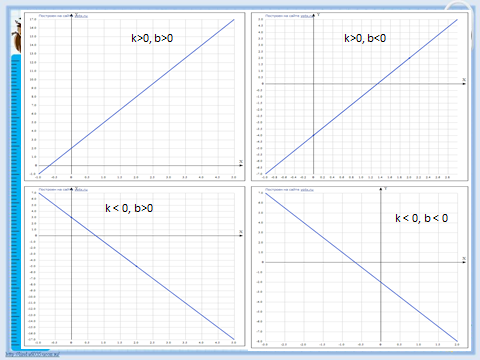
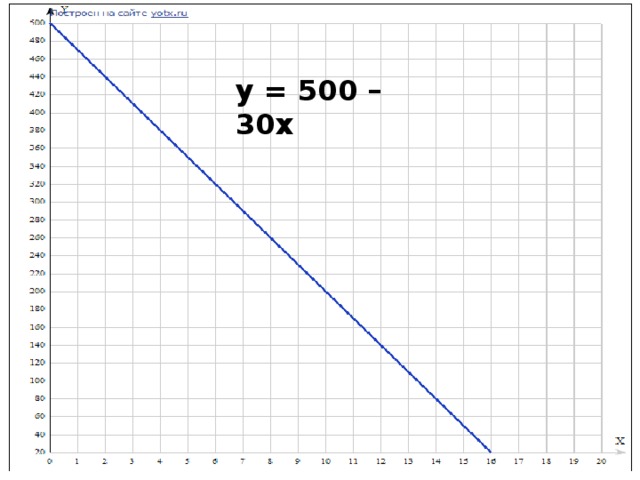
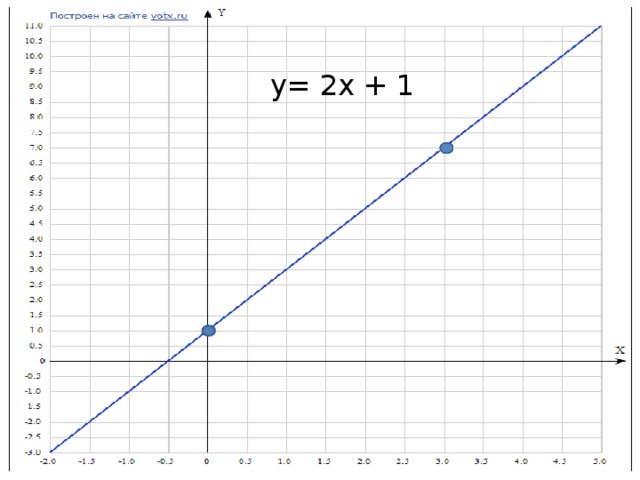
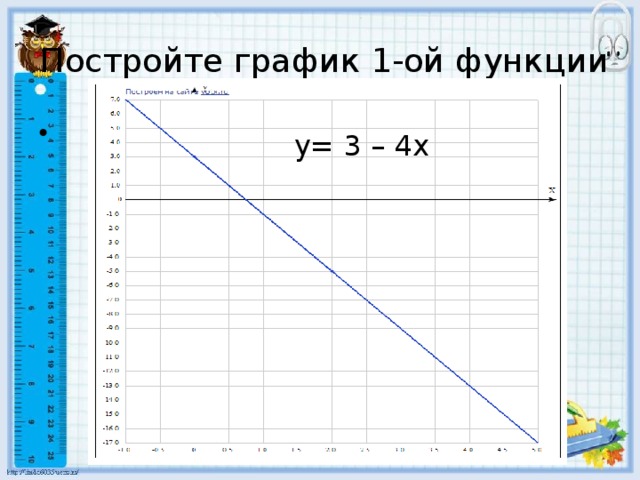
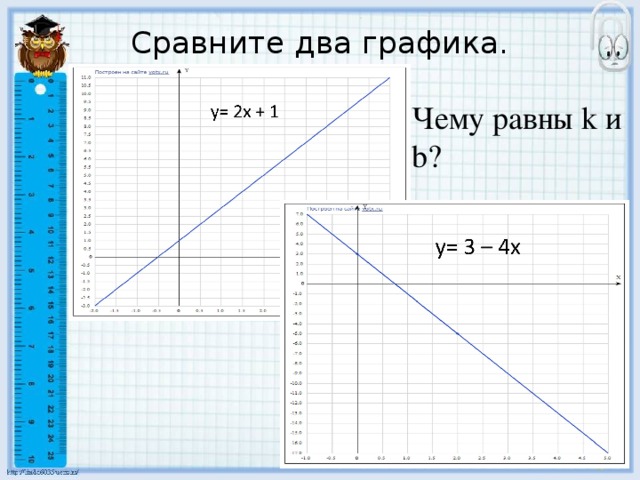
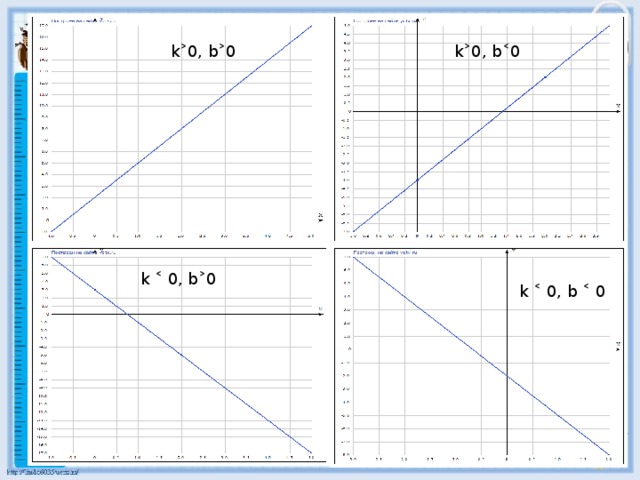
Линейная функция и её график. Конспект урока и презентация
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«информационная карта и конспект урока Линейная функция и её график»
Просмотр содержимого презентации
«Презентация к уроку линейная функция и ее график»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2100 руб.
3000 руб.
1900 руб.
2710 руб.
2100 руб.
3000 руб.
1670 руб.
2380 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства