Коммунальное учреждение «Общеобразовательная І-ІІІ ступеней школа №6
города Енакиево»
Конспект урока алгебры
«Квадратные уравнения»
8 класс
УМК любой
Учитель математики
Зубцова Валентина Петровна
2016-2017 учебный год
Урок обобщения и систематизации
по теме «Квадратные уравнения»
8 класс
Обоснование выбора
Возрастающая потребность связи математики и различных жизненных ситуаций побуждает учителя применять такие формы проведения уроков, которые бы могли донести знания до учащихся как можно интереснее и доступнее. Одной из таких форм является урок – обобщения и систематизации знаний, на котором школьники сами находят способы решения квадратных уравнений, обсуждают их решение, учатся критически мыслить, анализировать.
Методы обучения на уроке:
математические методы – моделирование, использование математического языка;
методы психологии – развитие мыслительных операций: анализ и синтез, классификация и систематизация, сравнение и обобщение;
методы педагогики – методы организации и стимулирования учебной деятельности;
информационные методы - использование презентации PowerPoint.
Актуальность поставленной цели урока.
При решении квадратных уравнений учащиеся используют в основном один способ, с помощью дискриминанта. О решении несколькими способами, как правило, не приходится говорить. Данный урок позволяет обобщить и рассмотреть различные способы решения квадратных уравнений изучаемых на уроках алгебры в разное учебное время; привести усвоенные способы в стройную систему. Конечным результатом усвоения таких систем знаний является сознательное овладение основными способами решения квадратных уравнений.
Место урока в тематическом планировании и системе уроков.
Преподавание ведётся по учебнику «Алгебра - 8»,Макарычев. В учебнике отдельно рассматриваются темы «Решение квадратных уравнений по формуле», «Теорема Виета», Данный урок позволяет обобщить все ранее изученные способы, так как к его проведению они умеют решать уравнения различными методами. В 9 классе после изучения темы: «График квадратичной функции» эта работа будет продолжена.
Форма организации деятельности учащихся.
На уроке я использую технологию индивидуально-бригадного обучения (ТИБО), технологию развития критического мышления (ТРКМ), а также технологию составления интеллект-карт. Индивидуальная, парная, групповая работа. Организация индивидуальной деятельности позволяет учитывать способности и образовательные потребности каждого, а коллективная (командная, бригадная) деятельность оказывает помощь каждому учащемуся в успешном освоении учебной программы. На данном уроке учащиеся разбиваются на группы по принципу личных симпатий для коллективной работы.
Организация учебной деятельности с учётом личностно - ориентированной технологии обучения.
На уроке созданы условия для реализации основных принципов личностно ориентированной технологии обучения. Это выражено в следующем:
создание атмосферы взаимной заинтересованности в работе учащихся и учителя;
стимулирование учащихся к высказываниям, использованию различных способов решения задачи без боязни ошибиться, получить неправильный ответ;
оценка деятельности ученика не только по конечному результату (правильно, неправильно), но и по процессу его достижения;
поощрение стремления ученика находить свой способ решения задачи, анализировать способы других учеников в ходе урока, выбирать и осваивать наиболее рациональные;
создание педагогических ситуаций межгруппового и внутригруппового общения на уроке, позволяющих каждому ученику проявлять инициативу, самостоятельность, избирательность в способах работы;
создание ситуации выбора и успеха;
создание обстановки для самовыражения ученика.
Использование ИКТ на данном уроке способствует:
решению всех задач урока: обучающих, развивающих, воспитательных;
повышению познавательной активности учащихся: развивается интерес к теме, каждый ученик на уроке занят делом, никто не бездельничает;
повышению интенсификации урока и темпа урока: презентация позволила значительно сократить время на обдумывание решения;
увеличению объёма выполненной работы.
Результат деятельности учащихся.
Результатом деятельности учащихся на уроке является понимание сути различных способов решения квадратных уравнений, осознанный и вдумчивый подход к анализу, поиску новых способов. Открытия для себя нового, осознание чувства сопричастности к общему успеху.
Цель урока:
Обобщение темы: «Квадратное уравнение»; создание условий для осознанного и уверенного владения навыком решения квадратных уравнений, рассмотрение различных способов решения квадратных уравнений.
Образовательные задачи урока:
систематизировать знания, выработать умение выбирать рациональный способ решения квадратных уравнений,
расширить и углубить представления учащихся о решении уравнений, организовать поисковую деятельность учащихся при решении квадратных уравнений;
создать условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений.
Развивающие задачи урока:
развивать математическое мышление, память, внимание;
развивать умение анализировать, сравнивать, обобщать, классифицировать, строить умозаключения, делать выводы;
развивать коммуникативные навыки; навыки самостоятельной работы;
развивать устную и письменную речь учащихся;
привить любовь к предмету, желание познать новое.
Воспитательные задачи урока:
воспитывать культуру умственного труда;
воспитывать культуру коллективной работы;
воспитывать информационную культуру;
воспитывать потребность добиваться успехов в приобретении знаний; воспитание навыков самоконтроля и взаимоконтроля, развитие самостоятельности и творчества.
Универсальные учебные действия:
Составление плана и последовательности действий.
Построение речевых высказываний.
Структурирование знаний.
Самооценка
Формы обучения: Индивидуальная, фронтальная работа, парная работа, групповая (коллективная) деятельность.
Оборудование:
Компьютер, мультимедийная установка, презентация, листы учета знаний, бумага и маркеры для рисования карты.
Ход урока.
| Структура и содержание |
Методы и приемы | Время |
|
1. Введение. Организационный момент. Предъявление темы и постановка задач урока.
2.Обобщение и систематизация знаний. Проверка домашнего задания Устная работа.
Фронтальный опрос.
Выполнение заданий. Работа в тетради.
Инструктаж учителя Работа в группах. Отчет о работе творческих групп 3.Домашнее задание. 4. Итог урока. 5. Рефлексия. |
Технология развития критического мышления
Интерактивное упражнение «Продолжи предложение»
Рисунок в тетради Беседа
Репродуктивный метод, самоконтроль. Частично – поисковый метод.
Исследовательский метод, Коллективный поиск. Технология составления интеллект-карт
Инструктаж учителя.
|
2-3 мин.
5 мин.
2-3 мин
5 мин.
10 мин.
5 мин 10 мин.
3 мин. 2 мин. 45 мин. |
Конспект урока
Организация работы класса.
На доске написано уравнение: «ах2 +вх+с=0» Посмотрите, ребята , на доску и подумайте, чем мы будем заниматься сегодня на уроке?
Ответы учеников:
-Решать уравнения
-Повторим различные способы решения
-Обязательно будет что-то новое
-Подготовимся к контрольной работе и т. д.
Учитель: Все ваши предположения верны! Мы повторим все, что знаем о квадратных уравнениях, о способах их решения, рассмотрим новые способы, научимся обобщать информацию, и составлять интеллект-карты. Ну, об этом в свое время.
Решение уравнений - это очень нужный инструмент в математике. Умение решать квадратные уравнения пригодятся вам в 9, 10 и 11 классах. И даже в высшей школе без них обойтись нельзя. Вот и получается, что от успеха на нашем уроке зависит ваш успех в изучении математики на всю вашу будущую жизнь. У каждого из вас на парте лежит «листок успеха», который вы будете заполнять по ходу урока: ставить себе отметки об участии в том или ином этапе урока.
Итак, вперед , к успеху!
Проверка домашнего задания. Дома вы выполняли самостоятельную работу по вариантам. Вам необходимо было решить 9 уравнений. Корни уравнений взять в качестве координат точек, отметить эти точки на координатной плоскости и соединить их отрезками последовательно. Посмотрим, что у вас получилось. (ребята поднимают тетради и по рисунку легко определить, все ли уравнения были решены правильно)
Повторение теоретического материала проведем в виде упражнения «продолжи предложение»
-Квадратным уравнением называется…
-Каждое из чисел а, в и с в квадратном уравнении называется…
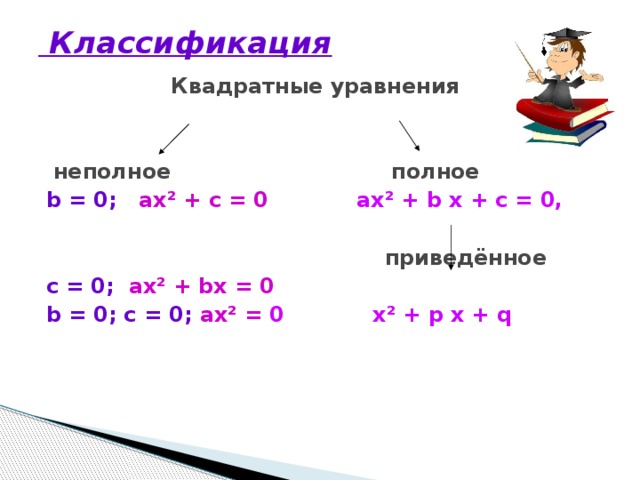
-Квадратные уравнения бывают…
-Если один из коэффициентов в или с или в и с равны 0, то уравнение называется…
-Количество корней полного квадратного уравнения можно определить с помощью…
- Дискриминантом квадратного уравнения называется…
-Уравнение имеет два корня, если…
-Уравнение не имеет корней, если…
- Если уравнение имеет корни, то их можно найти по формуле…
- Если в квадратном уравнении старший коэффициент равен 1, то уравнение называется…
- Сумма корней приведенного квадратного уравнения равна…
- Теорема, обратная теореме Виета гласит…
Учитель: По праву достойна в стихах быть воспета
О свойствах корней - теорема Виета.
Что лучше, скажи, постоянства такого-
Умножишь ты корни, и дробь уж готова:
В числителе «с» в знаменателе «а».
И сумма корней тоже дроби равна,
Хоть с минусом дробь та , ну что за беда:
В числителе «в», в знаменателе «а».
4. А теперь на практике вспомним, как решаются квадратные уравнения.
На экране вы видите, какие способы решения квадратных уравнений мы сегодня рассмотрим. Оцените критически свои умения пользоваться тем или иным способом. (Ребята высказывают свои мнения о своих знаниях). Какие из способов необходимо повторить?
Решить уравнение х2+10х +9 = 0 различными способами.
Используя формулу D
По формуле D1
По теореме, обратной теореме Виета
Выделением квадрата двучлена.
Графический способ
(5 человека работают у доски)
Какой из способов вам показался проще?
5.Новые сведения о решении квадратных уравнений
Посмотрите на экран, на слайде презентации утверждается, что по теореме, обратной теореме Виета можно решать лишь приведенные квадратные уравнения. А вот, Аня Денисенко с этим не согласна. И вот почему. (Ученица рассказывает, как решить уравнение перебросом старшего коэффициента):
Рассмотрим два уравнения: ах2+вх+с=0 и х2+вх +асх=0.Оба уравнения имеют равные дискриминанты – Д=в2- 4ас, а вот корни уравнений различны: х1,=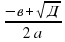 и х1=
и х1=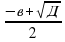 . Корни первого уравнения могут быть получены из корней второго уравнения делением на коэффициент а. Значит, для неприведенного квадратного уравнения можно составить вспомогательное уравнение х2+вх +асх=0, подобрать его корни по теореме, обратной к теореме Виета, и разделить каждый из них на а. Например: Для уравнения 2х2-5х+3=0 составляем вспомогательное х2-5х +2*3=0.Его корни х1=2, х2=3, тогда корни исходного уравнения х1=
. Корни первого уравнения могут быть получены из корней второго уравнения делением на коэффициент а. Значит, для неприведенного квадратного уравнения можно составить вспомогательное уравнение х2+вх +асх=0, подобрать его корни по теореме, обратной к теореме Виета, и разделить каждый из них на а. Например: Для уравнения 2х2-5х+3=0 составляем вспомогательное х2-5х +2*3=0.Его корни х1=2, х2=3, тогда корни исходного уравнения х1=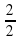 =1, х2=
=1, х2=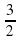 =1,5.
=1,5.
6.Познакомьтесь с новым способом решения квадратных уравнений «по коэффициентам»
Теорема 1: Если a+b+c=0, то x =1, x = 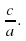
Примеры: 5x²-8x+3=0, так как 5-8+3=0, то Ответ: x =1; x = 3/5.
2) 3x²-7x+4=0; 3-7+4=0. Ответ: 1; 4/3.
Теорема 2: Если a-b+c=0, то x =-1, x ==- 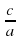 .
.
Примеры: 1)5x²+9x+4=0, 5-9+4=0, значит, х=-1, х=-4/5. Ответ: -1; -4/5
2) y²-22y-23=0, 1+22-23= 0 x =-1; x =- x =23. Ответ:-1; 23.
7.Самостоятельная работа.(по группам) 3 варианта- условие на слайде презентации. Взаимопроверка (результаты показаны на экране)
1) 3х² + 4х + 1 = 0,
2) 5х² - 4х – 9 = 0,
3) 6х² + 37х + 6 = 0,
4) 7х² + 2х – 5 = 0,
5) 13х² - 18х + 5 = 0,
6) 5х² + х – 6 = 0,
7) 7х² - 50х + 7 = 0,
8) 6х² - 37х + 6 = 0,
9) 7х² + 50х + 7 = 0.
Знакомство с правилами составления интеллект-карт. – объяснение учителя, необходимая информация размещена на слайде.
Работа над созданием интеллект-карты «Квадратные уравнения».
На слайде презентации вы видите пример составленной интеллект-карты по теме «Алгебраические дроби». Это должна быть красочная схема, отражающая весь учебный материал по теме «Квадратные уравнения» (виды уравнений, способы их решения, зависимости и связи).
6. Защита своего проекта.
7.Рефлексия:
«Закончи предложение»
- Сегодня я узнал…
- Было интересно…
- Я понял, что…
- Теперь я могу…
- Я научился…
- У меня получилось…
- Я попробую….
- Меня удивило…
- Мне захотелось…
Домашнее задание: повторить все способы решения уравнений, № 654 (учебник «Алгебра, 8 класс», Ю. Н. Макарычев), использовать все способы решения. Составить интеллект-карту с помощью компьютерных программ (для желающих).
Источники:
Учебник Алгебра 8 Ю.Н. Макарычев, Н.Г. Миндюк, К. И. Нешков М.: Просвещение ,2010
Дидактические материалы Алгебра 8, В. И. Жохов, Ю. Н. Макарычев, Н. Г. Миндюк М.: Просвещение, 2008
Конструирование современного урока математики. С.Г. Манвелов М.: Просвещение, 2005
Уроки математики с применением информационных технологий. 5-10 классы. Методическое пособие с электронным приложением / Л. Г. Горохова и др. – М: Издательство «Глобус»,2009. – (Современная школа).
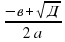 и х1=
и х1=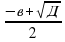 . Корни первого уравнения могут быть получены из корней второго уравнения делением на коэффициент а. Значит, для неприведенного квадратного уравнения можно составить вспомогательное уравнение х2+вх +асх=0, подобрать его корни по теореме, обратной к теореме Виета, и разделить каждый из них на а. Например: Для уравнения 2х2-5х+3=0 составляем вспомогательное х2-5х +2*3=0.Его корни х1=2, х2=3, тогда корни исходного уравнения х1=
. Корни первого уравнения могут быть получены из корней второго уравнения делением на коэффициент а. Значит, для неприведенного квадратного уравнения можно составить вспомогательное уравнение х2+вх +асх=0, подобрать его корни по теореме, обратной к теореме Виета, и разделить каждый из них на а. Например: Для уравнения 2х2-5х+3=0 составляем вспомогательное х2-5х +2*3=0.Его корни х1=2, х2=3, тогда корни исходного уравнения х1=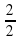 =1, х2=
=1, х2=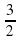 =1,5.
=1,5.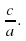
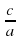 .
. 


 0 2корня" width="640"
0 2корня" width="640"