Конспект урока по теме "Решение задач по теме "Треугольники""

Тема: Решение задач

Тип урока: Урок практического применения знаний, умений и навыков

Цели:

Закрепление знаний учащихся по главе «Треугольники».
Развитие логического мышления.
Воспитание активности и самостоятельности.

Задачи:

Закрепить навыки в решении задач на применение признаков равенства треугольников.
Продолжить выработку навыков решения задач на построение с помощью циркуля и линейки.
Подготовить учащихся к предстоящей контрольной работе.

Оборудование:

Циркуль.
Линейка.
Карточки с проверочной работой.
Карточки с самостоятельной работой.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Конспект урока по теме "Решение задач по теме "Треугольники"" »

Г – 7 (Л. С. Атанасян)

Тема: Решение задач

Тип урока: Урок практического применения знаний, умений и навыков

Цели:

Закрепление знаний учащихся по главе «Треугольники».
Развитие логического мышления.
Воспитание активности и самостоятельности.

Задачи:

Закрепить навыки в решении задач на применение признаков равенства треугольников.
Продолжить выработку навыков решения задач на построение с помощью циркуля и линейки.
Подготовить учащихся к предстоящей контрольной работе.

Оборудование:

Циркуль.
Линейка.
Карточки с проверочной работой.
Карточки с самостоятельной работой.

Этапы

Ход урока

Примечание

Орг. момент

- Здравствуйте, садитесь.

- Сегодня мы на уроке закрепим навыки в решении задач на применение признаков равенства треугольников, решим задачи на построение и подготовимся к контрольной работе.

- А сперва проверим, как вы усвоили ранее изученный материал.

Актуализация прежних знаний

- Выполняем письменную работу на листочках по проверке решения задач на построение циркулем и линейкой:

Вариант 1

Отложить от данного луча угол, равный данному.
Построить середину данного отрезка.

Вариант 2

Построить биссектрису данного неразвернутого угла.
Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка.

В С

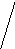
ешение задач

№ 152

Дано: АОВ – тупой.

Построить: ОХ: ХОА=ХОВ

Начертим тупой АОВ, построим биссектрису ОС этого угла и проведем продолжение ОХ луча ОС. Луч ОХ искомый. По построению ОС – биссектриса АОВ, АОС=ВОС=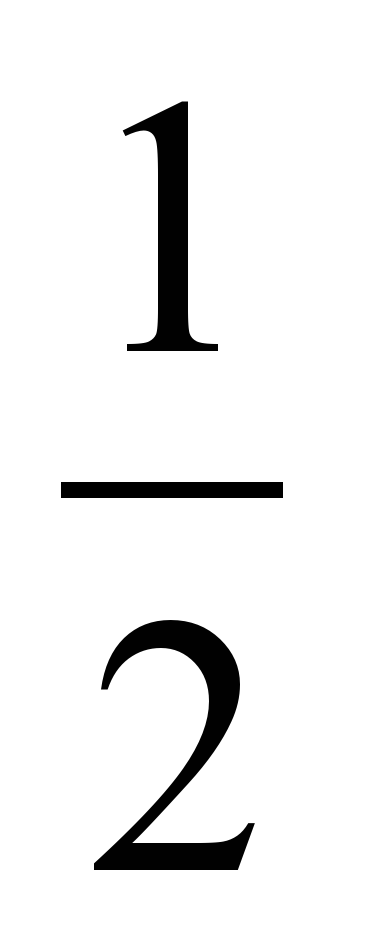АОВ и, АОС и ВОС – острые. АОС и АОХ, СОХ и ХОВ – смежные. (Сумма смежных углов равна 180)  АОС=ВОС  АОХ=ВОХ, т.к. АОС и ВОС – острые, то смежные с ними АОХ и ВОХ – тупые.

ешение:

Задача 1.

4х 4х

М 3х К

Дано: МДК, МД=ДК, МК:МД=3:4, Р=33 см.

Найти: МД, ДК, МК.

Решение: пусть х см – 1 часть, тогда МК=3х, Мд=ДК=4х. Р=33 см, значит 3х+4х+4х=33

11х=33

х=3

МК=9 см, МД=ДК=12 см.

В равнобедренном треугольнике основание относится к боковой стороне как 3:4. Найдите стороны этого треугольника, если периметр его равен 33 см.

Задача 2.

В равнобедренном треугольнике боковая сторона относится к основанию как 2:3. Найдите стороны этого треугольника, если периметр его равен 28 см.

(12 см, 8 см и 8 см.)

№

О Е

С х

175

Дано: ХОУ, т.А, СОХ, т.В, ДОУ,

АО=ОВ, АС=ВД, АДВС=Е.

Доказать: луч ОЕ – биссектриса ХОУ.

ОАД=ОВС (по 2 сторонам и углу между ними)1=2, 3=4.
3 и 5, 4 и 6 – смежные, 3=45=6.
ДВЕ=САЕ (по стороне и двум прилежащим углам)ВЕ=АЕ.
ОАЕ=ОВЕ (по трем сторонам) 7=8, т.е. ОЕ – биссектриса ХОУ

оказательство:

Для построения биссектрисы произвольного угла М на его сторонах откладываем отрезки МА=МВ, АС=ВД, и проведем отрезки АД и ВС. Затем проводим искомый луч МЕ, где Е – точка пересечения отрезков АД и ВС.

Самостоятельная работа

Вариант 1

На рисунке АВ=АС и ÐАСЕ=ÐАВД.

Докажите, что ∆АСЕ=∆АВД.
Найдите стороны треугольника АВД, если АЕ=15 см, ЕС=10 см, АС=7 см.

В Е

С Д

Вариант 2

На рисунке АО=СО и ÐВАО=ÐДСО.

Докажите, что ∆АОВ=∆СОД.
Найдите углы треугольника АОВ, если ÐОСД=37°, ÐОДС =63°, ÐСОД =80°.

А С

В Д

Домашнее задание

Подготовиться к контрольной работе,

№ 158

№ 166

№ 171

Итог урока

Сформулируйте I признак равенства треугольников.
Сформулируйте II признак равенства треугольников.
Сформулируйте III признак равенства треугольников.
Сформулируйте свойство углов равнобедренного треугольника.
Сформулируйте свойство биссектрисы, проведенный к основанию равнобедренного треугольника.

Раздается карточки.

На доске, вместе.

Раздается карточки.

Решение объясняется учителем на доске.

Самостоятельно.

На доске, вместе.

Раздается карточки.

Д/з на доске.

План доски

№ 152

№ 175

Классная работа.

Дома:

подг. контр. работе,

№ 158

№ 166

№ 171

Подпись методиста:

Предмет: Математика

Категория: Уроки

Целевая аудитория: 7 класс

Скачать
Конспект урока по теме "Решение задач по теме "Треугольники""

Автор: Бакунова Раина Рафаэлевна

Дата: 28.11.2014

Номер свидетельства: 136881

Похожие файлы

Конспект урока математики "Решение задач на нахождение четвертого пропорционального"

object(ArrayObject)#852 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(158) "Конспект урока математики "Решение задач на нахождение четвертого пропорционального""
    ["seo_title"] => string(80) "konspiekt_uroka_matiematiki_rieshieniie_zadach_na_nakhozhdieniie_chietviertogho_"
    ["file_id"] => string(6) "393270"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1487434775"
  }
}

Конспект урока по геометрии по теме «Практические приложения подобия треугольников».

object(ArrayObject)#874 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(159) "Конспект урока по геометрии по теме «Практические приложения подобия треугольников». "
    ["seo_title"] => string(96) "konspiekt-uroka-po-ghieomietrii-po-tiemie-praktichieskiie-prilozhieniia-podobiia-trieughol-nikov"
    ["file_id"] => string(6) "165571"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1422816467"
  }
}

Конспект урока геометрии по теме "Построение треугольника по трем элементам" с презентацией

object(ArrayObject)#852 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(170) "Конспект урока геометрии по теме "Построение треугольника по трем элементам" с презентацией "
    ["seo_title"] => string(106) "konspiekt-uroka-ghieomietrii-po-tiemie-postroieniie-trieughol-nika-po-triem-eliemientam-s-priezientatsiiei"
    ["file_id"] => string(6) "122600"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1414307092"
  }
}

Конспект урока на тему " Свойства прямоугольного треугольника"

object(ArrayObject)#874 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(116) "Конспект урока на тему " Свойства прямоугольного треугольника" "
    ["seo_title"] => string(66) "konspiekt-uroka-na-tiemu-svoistva-priamoughol-nogho-trieughol-nika"
    ["file_id"] => string(6) "102353"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1402499505"
  }
}

конспект урока на тему "Сумма углов треугольника"

object(ArrayObject)#852 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(90) "конспект урока на тему "Сумма углов треугольника""
    ["seo_title"] => string(45) "konspiekturokanatiemusummaughlovtrieugholnika"
    ["file_id"] => string(6) "289747"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1454856484"
  }
}

Конспект урока по теме "Решение задач по теме "Треугольники""

Просмотр содержимого документа «Конспект урока по теме "Решение задач по теме "Треугольники"" »

Похожие файлы

Полезное для учителя

Просмотр содержимого документа
«Конспект урока по теме "Решение задач по теме "Треугольники"" »