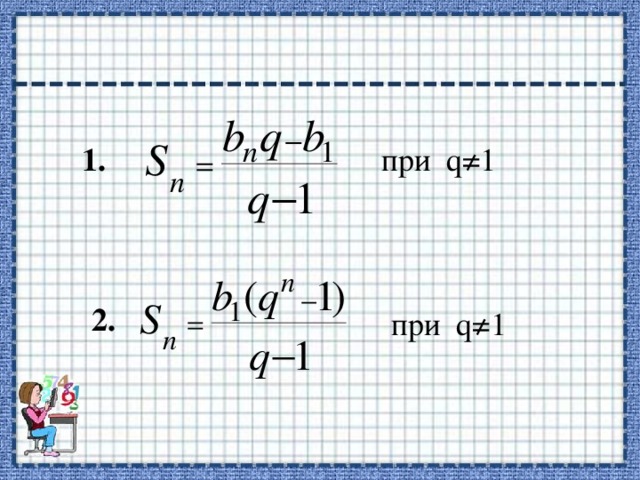Урок по теме: «Формула суммы n-первых членов геометрической прогрессии»
Цель: вывести формулу сумму n первых членов геометрической прогрессии; выработать навыки нахождении суммы n первых членов геометрической прогрессии.
Задачи:
- формирование навыков применения формулы при решении заданий;
- развивать логическое мышление, правильной устной и письменной математической речи, развитие кругозора;
- воспитывать интерес к предмету, ответственности, трудолюбия.
Структура урока:
- Организационный момент
- Актуализация опорных знаний
- Изучение нового материала
- Первична проверка понимания
- Подведение итогов урока
- Сообщение домашнего задания
Ход урока
- Организационный момент
Здравствуйте, ребята. Настраиваемся на рабочий лад, начинаем.
- Актуализация опорных знаний
Ребята у вас на столах лежат листы опроса. Заполните их. Времени вам 7-10 минут.
() – геометрическая прогрессия
1.Определение
2. Формула n-ого члена
- Решите тест
1. В геометрической прогрессии b5=12 b7 =27
b6 -?
A) 19,5
Б) 25
В) 18
Г) 36
- Изучение нового материала
Ребята откройте тетради, запишите число, классная работа, тему урока: «Формула суммы n-первых членов геометрической прогрессии».
Цель нашего урока изучить формулы для нахождения суммы геометрической прогрессии и научиться применять данную формулу при решении заданий.
Ребята, сегодня я хоте бы вас познакомить с легендой «о шахматной доске». У вас на столах лежат листы, придвиньте их к себе и внимательно прочитайте.
«Шахматы – одна из самых древних игр. Она существует уже многие века и неудивительно, что с нею связаны различные придания, правдивость которых, за давностью времени, невозможно проверить.
Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений.
Легенда о шахматной доске
Шахматы – одна из самых древних игр. Она существует уже многие века и неудивительно, что с нею связаны различные придания, правдивость которых, за давностью времени, невозможно проверить.
Чтобы понять ее, не нужно вовсе уметь играть в шахматы: достаточно точно знать, что игра происходит на доске, разделенной на 64 клетки (попеременно черные и белые).
Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений.
Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.
Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.
– Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал, – сказал царь. Я достаточно богат, чтобы исполнить самое смелое твое пожелание – предложил царь.
– Назови награду, которая тебя удовлетворит, и ты получишь ее.
Сета молчал.
– Не робей, – ободрил его царь. – Выскажи свое пожелание. Я не пожалею ничего, чтобы исполнить его.
На что Сета сказал, что он обдумает ответ и завтра сообщит царю свою просьбу.
На другой день, когда Сета сообщил свою просьбу, царь удивился беспримерной скромности бедного Мудреца.
– Повелитель, – сказал Сета, – прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.
– Простое пшеничное зерно? – изумился царь.
– Да, повелитель. За вторую клетку выдать 2 зерна, за третью – 4, за четвертую – 8, за пятую – 16, за шестую – 32…
– Довольно, – с раздражением прервал его царь. Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию. Но знай, что твоя просьба недостойна моей щедрости. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Слуги мои вынесут тебе твой мешок с пшеницей.
Царь Шерам засмеялся.»
Ребята Как велико это число? Кто может объяснить?
Переверните листы и посмотрите что за запись должна быть из этой легенды. (запись на доске 1, 2,8, 16, 32, . . . S64 - ?)
Учащиеся: Решают: b1=1; q=2; n=64.
S= ; S64=264 – 1
Сможем ли мы ребята не зная формулы вычислить? А ученые вычислили и получили следующее число (оно тоже записано на обратной стороне листа)
18 квинтиллионов 446 квадриллионов 744 триллиона 73 миллиарда 709 миллионов 551 тысяча 615.
Таким образом была выведена следующая формула:
- , при q1Место для формулы.
- , при q1
Рассмотрим пример
Дана геометрическая последовательность
Известно, что b1=3, q=2, n=6. Найдите сумму членов прогрессии.
- Первичная проверка понимания.
Ребята разобьемся на группы:
1 группа: Веселков С, Павлова Н, Иванов П, Симонова А, Фартусов Д
2 группа: Туманова Н, Веселкова А, Каверзина И, Астраханцева Т.
3 Группа: Якимов А, Пинигина И, Тимофеев С, Лыткин С, Зырянов А
1 группа выполняет № 17. 28 (в)
2 группа выполняет № 17. 25 (б)
3 группа выполняет № 17.12 (г)
Проверяем….
Ребята вы знаете, что данная тема встречается в ГИА. Давайте выполним задания из ГИА.
КИМ -2013.
- Геометрическая прогрессия задана несколькими первыми членами: 2;
-3; 18; ….. Найдите сумму первых пяти её членов.
2. Геометрическая прогрессия задана своим первым членом в1 =256 и знаменателем q=. Найдите девятый член этой прогрессии.
3. Геометрическая прогрессия задана своим вторым и пятым членами:
b1 = 1; b5 = 8. Найдите сумму первых семи её членов.
Проверяем….
- Подведение итогов
Ребята у вас на столах лежат листы с табличкой. Вы должны закончить фразы…
Я проанализирую данную таблицу, а на следующем уроке мы доработаем, то что вам было не понятно.
- сегодня я узнал……
- было трудно……
- я научился……
- мне захотелось……
- Домашнее задание
1 группа - № 17.29 (в), № 17.41 (а)
2 группа - № 17.25 (а), № 17.27 (а)
3 группа - № 17.19 (а, в
Просмотр содержимого документа
«Урок по теме геометрическая прогрессия»
Урок по теме: «Формула суммы n-первых членов геометрической прогрессии»
Цель: вывести формулу сумму n первых членов геометрической прогрессии; выработать навыки нахождении суммы n первых членов геометрической прогрессии.
Задачи:
- формирование навыков применения формулы при решении заданий;
- развивать логическое мышление, правильной устной и письменной математической речи, развитие кругозора;
- воспитывать интерес к предмету, ответственности, трудолюбия.
Структура урока:
Организационный момент
Актуализация опорных знаний
Изучение нового материала
Первична проверка понимания
Подведение итогов урока
Сообщение домашнего задания
Ход урока
Организационный момент
Здравствуйте, ребята. Настраиваемся на рабочий лад, начинаем.
Актуализация опорных знаний
Ребята у вас на столах лежат листы опроса. Заполните их. Времени вам 7-10 минут.
|
| (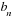 ) – геометрическая прогрессия ) – геометрическая прогрессия |
| 1.Определение | 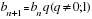
|
| 2. Формула n-ого члена | 
|
Решите тест | 1. В геометрической прогрессии b5=12 b7 =27 b6 -? A) 19,5 Б) 25 В) 18 Г) 36 |
Изучение нового материала
Ребята откройте тетради, запишите число, классная работа, тему урока: «Формула суммы n-первых членов геометрической прогрессии».
Цель нашего урока изучить формулы для нахождения суммы геометрической прогрессии и научиться применять данную формулу при решении заданий.
Ребята, сегодня я хоте бы вас познакомить с легендой «о шахматной доске». У вас на столах лежат листы, придвиньте их к себе и внимательно прочитайте.
«Шахматы – одна из самых древних игр. Она существует уже многие века и неудивительно, что с нею связаны различные придания, правдивость которых, за давностью времени, невозможно проверить.
Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений.
Легенда о шахматной доске
Шахматы – одна из самых древних игр. Она существует уже многие века и неудивительно, что с нею связаны различные придания, правдивость которых, за давностью времени, невозможно проверить.
Чтобы понять ее, не нужно вовсе уметь играть в шахматы: достаточно точно знать, что игра происходит на доске, разделенной на 64 клетки (попеременно черные и белые).
Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений.
Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.
Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.
– Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал, – сказал царь. Я достаточно богат, чтобы исполнить самое смелое твое пожелание – предложил царь.
– Назови награду, которая тебя удовлетворит, и ты получишь ее.
Сета молчал.
– Не робей, – ободрил его царь. – Выскажи свое пожелание. Я не пожалею ничего, чтобы исполнить его.
На что Сета сказал, что он обдумает ответ и завтра сообщит царю свою просьбу.
На другой день, когда Сета сообщил свою просьбу, царь удивился беспримерной скромности бедного Мудреца.
– Повелитель, – сказал Сета, – прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.
– Простое пшеничное зерно? – изумился царь.
– Да, повелитель. За вторую клетку выдать 2 зерна, за третью – 4, за четвертую – 8, за пятую – 16, за шестую – 32…
– Довольно, – с раздражением прервал его царь. Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию. Но знай, что твоя просьба недостойна моей щедрости. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Слуги мои вынесут тебе твой мешок с пшеницей.
Царь Шерам засмеялся.»
Ребята Как велико это число? Кто может объяснить?
Переверните листы и посмотрите что за запись должна быть из этой легенды. (запись на доске 1, 2,8, 16, 32, . . . S64 - ?)
Учащиеся: Решают: b1=1; q=2; n=64.
S= ; S64=264 – 1
Сможем ли мы ребята не зная формулы вычислить? А ученые вычислили и получили следующее число (оно тоже записано на обратной стороне листа)
18 квинтиллионов 446 квадриллионов 744 триллиона 73 миллиарда 709 миллионов 551 тысяча 615.
Таким образом была выведена следующая формула:
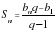 , при q
, при q
 1Место для формулы.
1Место для формулы.
 , при q
, при q
 1
1
Рассмотрим пример
Дана геометрическая последовательность
Известно, что b1=3, q=2, n=6. Найдите сумму членов прогрессии.
Первичная проверка понимания.
Ребята разобьемся на группы:
1 группа: Веселков С, Павлова Н, Иванов П, Симонова А, Фартусов Д
2 группа: Туманова Н, Веселкова А, Каверзина И, Астраханцева Т.
3 Группа: Якимов А, Пинигина И, Тимофеев С, Лыткин С, Зырянов А
1 группа выполняет № 17. 28 (в)
2 группа выполняет № 17. 25 (б)
3 группа выполняет № 17.12 (г)
Проверяем….
Ребята вы знаете, что данная тема встречается в ГИА. Давайте выполним задания из ГИА.
КИМ -2013.
Геометрическая прогрессия задана несколькими первыми членами: 2;
-3; 18; ….. Найдите сумму первых пяти её членов.
2. Геометрическая прогрессия задана своим первым членом в1 =256 и знаменателем q=
 . Найдите девятый член этой прогрессии.
. Найдите девятый член этой прогрессии.
3. Геометрическая прогрессия задана своим вторым и пятым членами:
b1 = 1; b5 = 8. Найдите сумму первых семи её членов.
Проверяем….
Подведение итогов
Ребята у вас на столах лежат листы с табличкой. Вы должны закончить фразы…
Я проанализирую данную таблицу, а на следующем уроке мы доработаем, то что вам было не понятно.
|
- сегодня я узнал……
|
|
|
- было трудно…… |
|
|
- я научился……
|
|
| - мне захотелось……
|
|
Домашнее задание
1 группа - № 17.29 (в), № 17.41 (а)
2 группа - № 17.25 (а), № 17.27 (а)
3 группа - № 17.19 (а, в)
Просмотр содержимого презентации
«геометрическая прогрессия»
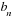 ) – геометрическая прогрессия
) – геометрическая прогрессия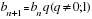

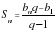 , при
, при 
 , при
, при