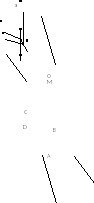Тема: ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Цели:
- Сформировать у обучающихся понятие перпендикулярности прямых в пространстве, прямой перпендикулярной плоскости; изучить лемму о перпендикулярности двух параллельных прямых третьей; теоремы в которых устанавливается связь между параллельностью прямых и их перпендикулярностью к плоскости.
- Продолжить формирование навыков самостоятельности у обучающихся в процессе самоконтроля и при изучении нового материала.
- Воспитывать познавательный интерес к предмету.
Методическая цель:
Активизация познавательной деятельности обучающихся на уроке математики.
КМО:
- Рисунки к теоремам
- Справочный материал
- Рисунки к задачам (подготовленные обучающимися)
- учебник
- карта отметок
Тип урока:
Изучение нового материала.
Вид урока:
Комбинированный.
Ход урока.
- Орг. момент.
- Подготовка обучающихся к занятию.
Сообщение темы и цели занятия. Мотивация.
- Формирование новых знаний.
Работа с обучающимися получившими опережающее задание.
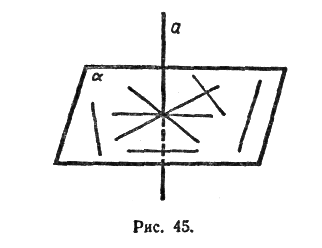
1 обучающийся: Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90°. Перпендикулярность прямых а и b обозначается так: а^b. Перпендикулярные прямые могут пересекаться и могут быть
скрещивающимися. На рисунке1 перпендикулярные прямые а и b пересекаются, а перпендикулярные прямые а и с скрещивающиеся.
2 обучающийся: Докажем лемму о перпендикулярности двух параллельных прямых к третьей прямой.
Лемма. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Доказательство. Пусть а||b и a^c. Докажем, что b^с. Через произвольную точку М пространства, не лежащую на данных прямых, проведем прямые МА и МС, параллельные соответственно прямым а и с (рис. 2). Так как a^c, то ÐAMC = 90°.
Рисунок 1
Рисунок 2
По условию леммы b||а, а по построению а||МA, поэтому b||МА. Таким образом, прямые b и с параллельны соответственно прямым МА и МС, угол между которыми равен 90°. Это означает, что угол между прямыми b и с также равен 90°, т. е. b^c. Лемма доказана.
Оформление в тетради:
Дано:
а||b, a^c
Доказать:
b^с
Доказательство:
1. Через точку М Îa, МА|| a, МС|| c, a ^ cÞ ÞМА^МСÞÐAMC=90°.
2. b||а, а||МAÞ b||МАÞ b^c.
3 обучающийся: Параллельные прямые, перпендикулярные к плоскости. Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Перпендикулярность прямой а и плоскости a обозначается так: a^a. Говорят также, что плоскость a, перпендикулярна к прямой а.
Если прямая а перпендикулярна к плоскости a, то она пересекает эту плоскость. В самом деле, если бы прямая а не пересекала плоскость a, то она или лежала бы в этой плоскости, или была бы параллельна ей. Но тогда в плоскости a имелись бы прямые, не перпендикулярные к прямой а, например прямые, параллельные ей, что противоречит определению перпендикулярности прямой и плоскости. Значит, прямая а пересекает плоскость a.
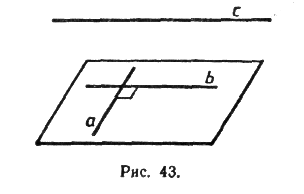
На рисунке 3 изображена прямая а, перпендикулярная к плоскости a.
Окружающая нас обстановка дает много примеров, иллюстрирующих перпендикулярность прямой и плоскости. Непокосившийся телеграфный столб стоит прямо, т. е. перпендикулярно к плоскости земли. Так же расположены колонны здания по отношению к плоскости фундамента, линии пересечения стен по отношению к плоскости пола и т. д.
Докажем две теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярностью к плоскости.
Рисунок 3
Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости,
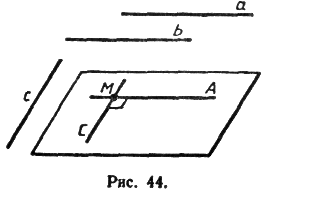
Рисунок 4
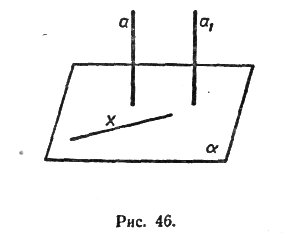
Доказательство. Рассмотрим две параллельные прямые а и a1 и плоскость a, такую, что a^a. Докажем, что и a1^a.
Проведем какую-нибудь прямую х в плоскости a (рис. 4). Так как a^a, то a^x. По лемме о перпендикулярности двух параллельных прямых к третьей a1^x. Таким образом, прямая a1 перпендикулярна к любой прямой, лежащей в плоскости a, т. е. a1^a. Теорема доказана.
Оформление в тетради:
Дано:
а|| a1, a^a
Доказать:
a1^a
Доказательство:
Проведём х Îa, т.к. a^a, то a ^хÞ a1^ х (лемма) Þ Þa1^a..
Докажем обратную теорему.
Теорема. Если две прямые перпендикулярны к плоскости, то они параллельны.
Рисунок 5
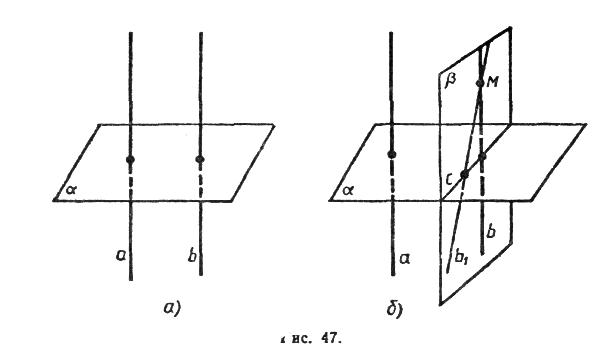
Доказательство. Рассмотрим прямые а и b, перпендикулярные к плоскости a (рис. 5,а). Докажем, что а || b.
Через какую-нибудь точку М прямой b проведем прямую b1, параллельную прямой а. По предыдущей теореме b1^a. Докажем, что прямая b1 совпадает с прямой b. Тем самым будет доказано, что а || b. Допустим, что прямые b и b1 не совпадают. Тогда в плоскости b, содержащей прямые b и b1, через точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости a иb (рис. 5, б). Но это невозможно, следовательно, а||b. Теорема доказана.
Оформление в тетради:
Дано:
a^a, b^a
Доказать:
а || b
Доказательство:
1.Предположим, что а || b тогда, через М Îb, b1 ||aÞ Þa^a Þ b1^a.
2. через точку М в плоскости b, b и b1 ^с Þ а || b
- Закрепление нового материала.
1. Чтение теорем устанавливающих связь между параллельностью и перпендикулярностью.
2. Попарная проверка теорем.
- Применение знаний и умений обучающихся.
Заранее выбираются консультанты, которые разбирают задачи и выполняют рисунки к ним.
Группа делится на подгруппы, где вместе с консультантами разбираются задачи. От каждой группы представитель записывает решение задачи у доски. Все обучающиеся записывают решения задач в тетрадь.
- подгруппа №116(а).
- подгруппа №116 (б).
- подгруппа №117
- Подгруппа №118
- Подгруппа №117
- Домашнее задание.
- Подведение итогов занятия(выставление отметок).
Приложение
№ 116 (а)
Дано: - параллелепипед,
Доказать: ,
Доказательство: A1D1ïïAD Þ AB^ A1D1 (лемма);
ABïïDC, B1C1ïïAD Þ DC^B1C1 (лемма).
№ 116 (б)
Дано: - параллелепипед, AB^DD1
Доказать: ,
Доказательство: ABïïA1B1, AB^DD1 Þ A1B1^ DD1 (лемма);
AB^DD1, DD1ïïCC1 Þ AB^CC1 (лемма).
№ 117
Дано: DABC - тетраэдр, BC^AD, MÎAB, AM = MB, NÎAC, AN = NC
Доказать: AD^MN
Доказательство: MNïïBC, (как средняя линия D ABC);
BC^AD Þ MN^AD (лемма).
№ 118
Дано: a^a, A,M, O Î a, O,B,C,D Î a
Найти: прямые углы
Решение: a^a Þ a^CO, a^ DO, a^BO (по определению перпендикулярности прямой и плоскости) Þ ÐAOB = 90º,
ÐMOC = 90º, ÐDOA = 90º


 - параллелепипед,
- параллелепипед, 
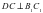 ,
, 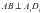

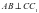 ,
,