Данный урок алгебры и начала анализа - это урок изучения нового материала по теме: "Понятие логарифма". Урок разработан с использованием презентации, структура урока соответсвует ФГОС. В ходе рока ребята занкомятся с понятием логарифма, с историей его возникновения, практическим применением. Входе урока используется тест, разработанный для выявления уровня освоения новых знаний и умений.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Конспект урока и презентация по теме: "Понятие логарифма".
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«конспект открытого урока понятие логарифма 10 класс»
Учитель математики: Нуждина Алёна Владимировна
Предмет: алгебра и начала анализа
Класс: 10
Тема урока: «Понятие логарифма»
Цели урока:
Личностные:
1) формирование представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
2) формирование основ саморазвития, самовоспитания, готовности и способности к самостоятельной, творческой и ответственной деятельности;
3) формирование готовности и способности вести диалог с другими людьми, достигать в нем взаимопонимания, находить общие цели и сотрудничать для их достижения;
4) формирование умений ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
5) формирование креативности мышления, инициативы, активности.
Метапредметные:
1)формирование умения самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность;
2) формирование умения продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности;
3) формирование навыков познавательной, учебно-исследовательской деятельности, навыков разрешения проблем; способности и готовности к самостоятельному поиску методов решения практических задач;
4) формирование умения использовать средства информационных и коммуникационных технологий в решении задач;
5) формирование умения понимать и использовать в решении математические средства (графики, таблицы) для иллюстрации, интерпретации, аргументации;
6) формировать умения владеть языковыми средствами - умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства.
3. Предметные:
1) формировать представления о социальных, культурных и исторических факторах становления математики;
2) формировать основы логического, алгоритмического и математического мышления;
3) формировать умения применять полученные знания при решении различных задач;
4) изучить понятия логарифм, натуральный логарифм, десятичный логарифм;
5) формирование навыка вычисления логарифма, используя определение логарифма;
6) формирование навыка работы с готовыми компьютерными программами при решении задач.
Этапы урока:
Актуализация знаний по теме «Степень положительного числа». (7мин)
Изучение нового материала. (20 мин)
Практическая работа с учебником. (8мин)
Проверочная работа (он-лайн тестирование). (7 мин)
Подведение итогов и задание на дом. (3мин)
Оборудование урока:
Доска, мультимедийный проектор, ноутбуки, компьютеры, учебник, логарифмические линейки, листы самооценки.
Ход урока:
Актуализация знаний, фронтальный опрос.
- Вспомните основные свойства степени с рациональным показателем.
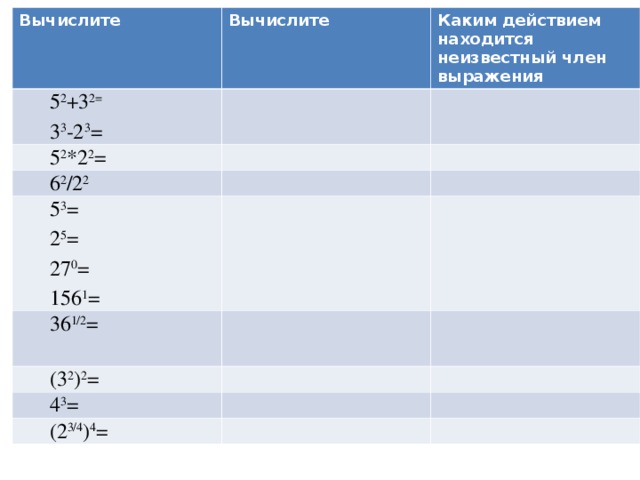
- Устно вычислите: (см. слайды 1-3)
|
|
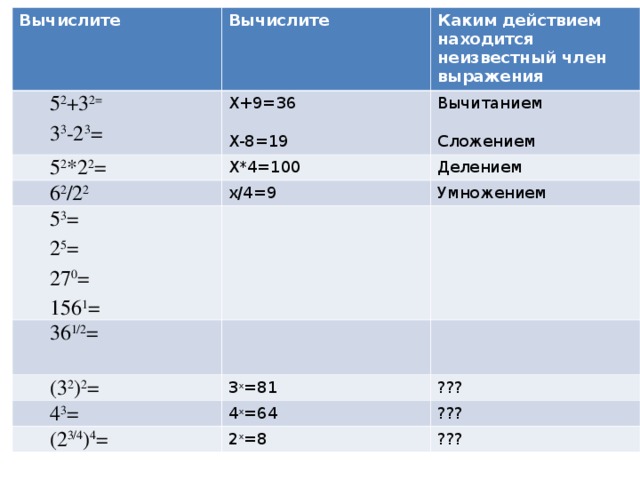
| Каким действием находится неизвестный член |
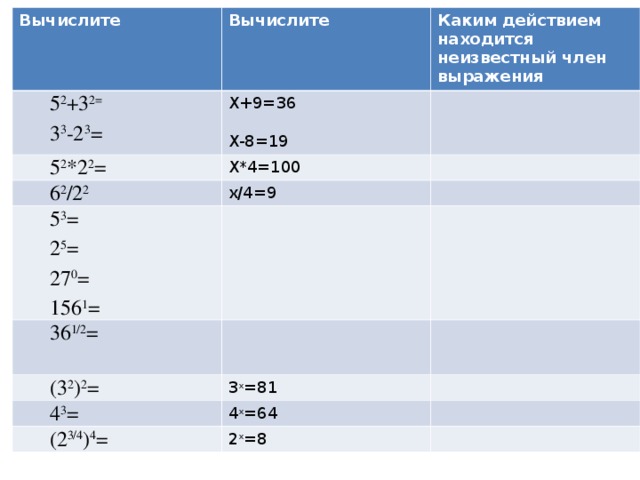
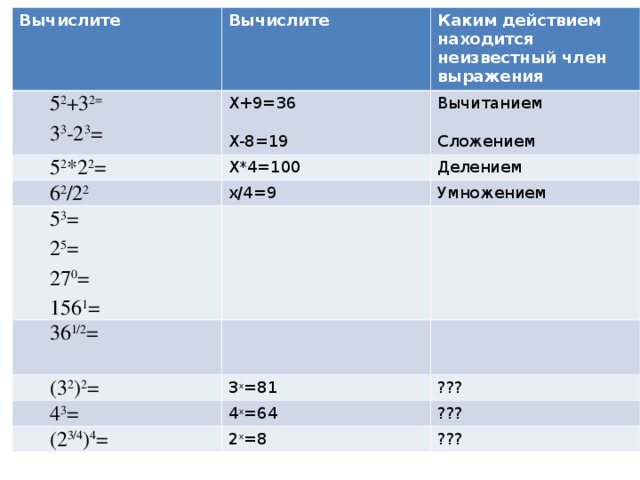
| 52+32=25+9=36 | Х+9=36 | вычитанием |
| 33-23=27-8=19 | Х-8=19 | сложением |
| 52*22=25*4=100 | Х*4=100 | делением |
| 62 = 36/4=9 22 | х/4=9 | умножением |
| 53=125 25=32 270=1 1561=156 |
|
|
| 361/2=(62)0,5=6
|
|
|
|
|
|
|
| (32)2=34=81 | 3х=81 | ??? |
| 43=64 | 4х=64 | ??? |
| (23/4)4=23=8 | 2х=8 | ??? |
Вопрос: чему равен неизвестный показатель? И как называется такое действие?
Предположительный ответ: х=4, х=3, х=2, нашли подбором.
Вы считаете, что подбором можно решить любое показательное уравнение? (Да)
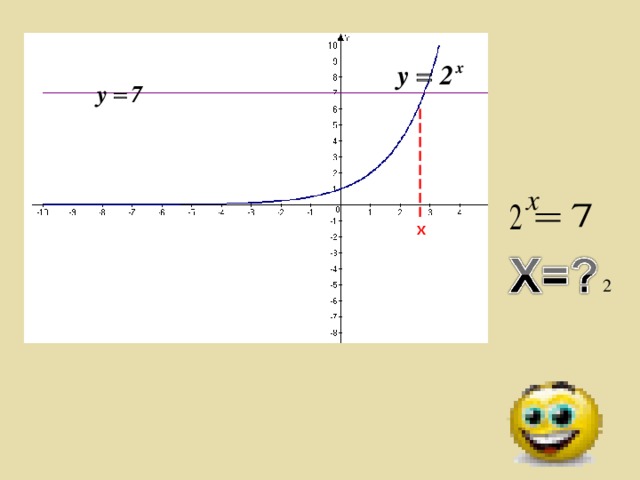
Решите: 2х=7 (Нет решений)
Вспомните, как выглядит график показательной функции y=ax, где а0, a
1. (см. слайд №4). Из графиков видно, что показательная функция определена на всей оси Ох, т.е. х может принимать любые значения, а у0. Следовательно, если мы возьмем на оси Оу значение 7, то на оси Ох найдется соответственная точка. Значит - решение есть. Этот способ решения называется графическим. А другой способ решения есть? Можно ли как-то еще найти показатель степени?
Изучение нового материала.
Показатель степени можно найти и другим способом. Существует такое понятие как логарифм. Как вы думаете, какая тема нашего урока? (Логарифмы). Тема урока – Понятие логарифма (слайд 5).
Какую цель мы должны поставить на сегодняшний урок? (Узнать, что такое логарифм и научиться его вычислять) (слайд 6).
Поэтому наш урок мы разделим на 3 этапа: изучение понятия логарифма, изучение способа вычисления логарифма, проверочный – как вы это всё поняли. Перед вами листы самооценки: в них вы за каждый этап урока должны поставить себе отметку – оценить себя, насколько успешно вы овладели понятиями по данной теме, как вы научились находить логарифм, и последняя отметка – это то, что вы получите за проверочную работу в форме он-лайн теста.
Итак, что же такое логарифм и как его вычислять?
Логарифмом положительного числа b по основанию а (где а0, а1) называют показатель степени 
, такое, что b=a, обозначается log ab=(слайд 7).
Из определения логарифма следует следующее тождество: a log ab=b, данное тождество называют – основное логарифмическое тождество (слайд 8,9).
Вернёмся к таблице, вы не заполнили 3 столбец, как называется действие обратное возведению в степень? (слайд10,11)
Как вы думаете, для чего изобрели логарифмы? (???) (слайд 12-14).
Ещё в 16 – 17 веке с развитием дальнего мореплавания (это эпоха – великих географических открытий) возникла большая потребность в вычислениях, тогда еще не было сложных навигационных приборов, ориентироваться мореплавателям приходилось по звездам, а значит, нужны были сложные астрономические расчеты с многозначными числами. Вычислять необходимо было много и точно, и астрономы задумались над тем, как же упростить вычисления? Так были созданы различные таблицы, которыми, единожды произведя точные вычисления, можно пользоваться бесконечное число раз
В начале урока вы вспомнили свойства степеней, где при умножении степеней с одинаковым основанием показатели складываются, а при делении показатели вычитаются. Давайте мы с вами создадим одну из таких таблиц, на пример для основания 2.
| (Показатель степени) ЛОГАРИФМ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| число | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
Посмотрите, как с помощью созданной вами таблицы легко вычислить, например: 32*128=25*27=212=4096. Мы от умножения перешли к сложению степеней, т.е. работали с показателем – логарифмом.
Вычислите 16*64; т.е. 4+6=10 значит, 16*64=1024
Вычислите 512:32, при делении показатели вычитаются, т.е. 9-5=4, 512:32=16
Ученые создали целые тома для вычисления логарифмов. Кроме того, для облегчения вычисления была создана логарифмическая линейка, позволяющая производит множества действий: возведение в квадрат, куб, находить логарифмы (показатели степени), синусы, косинусы и многое другое. Давайте рассмотрим, как используя логарифмическую линейку легко найти квадрат, куб числа. (Работа с линейкой)
Итак, логарифм – это показатель степени, в которую нужно возвести число а, что бы получить число b.
Логарифм положительного числа b по основанию е=2,7 называют натуральным логарифмом числа b и обозначают ln b, т.е. вместо log e b пишут ln b.
Логарифм положительного числа b по основанию 10 называют десятичным логарифмом числа b и обозначают lg b, т.е. вместо log 10 b пишут lg b.
Откройте учебник на странице 149, прочитайте еще раз определения логарифма, десятичного, натурального запомните и расскажите их друг другу. Оцените ответ соседа по парте на листе самооценки.
Как справились с первым этапом? Достигли поставленной цели – изучить понятие логарифма?
Практическая работа. Работа с учебником, один работает у доски остальные в тетради.
Прочитайте и выполните задание №5.4 (а,в,г,д,е), 5.5 (а,б,ж). Оцените свою работу, если все выполнили самостоятельно и правильно, то поставьте себе 5, если допустили ошибку – 4. Если работали вместе с доской, то – 3.
4.Проверочная работа.
Давайте проверим, как вы научились вычислять логарифмы, используя определение логарифма, основное логарифмическое тождество. Откройте на компьютере Google, введите в поисковой строке адрес http://letstest.ru/testpanel/exams/start/19921.
Перед вами он-лайн тест, введите свое имя, фамилию, класс. На выполнение теста вам дается не более 7 минут. Тест состоит из заданий двух типов: введение текстового ответа (слова) и выбора правильного ответа из 4-х предложенных. За тест вы получите отметку, скопируйте ее на свой оценочный лист. Вычислите среднее арифметическое трех отметок и поставьте данную отметку себе за урок.
Что нового узнали вы на уроке? Для чего нужны логарифмы? Достигли ли вы поставленной вначале урока цели? Если нет то, что необходимо сделать дома? (выучить определение логарифма, научиться вычислять логарифмы выполнив задания из учебника №5.7-5.9 (а,г,ж)).
Просмотр содержимого документа
«лист самооценки»
Просмотр содержимого документа
«таблица логарифмическая для основани2»
Просмотр содержимого презентации
«Логарифм числа»
Вычислите
5 2 +3 2=
3 3 -2 3 =
Вычислите
5 2 *2 2 =
Каким действием находится неизвестный член выражения
6 2 /2 2
5 3 =
2 5 =
27 0 =
156 1 =
36 1/2 =
(3 2 ) 2 =
4 3 =
(2 3/4 ) 4 =
Вычислите
5 2 +3 2=
3 3 -2 3 =
Вычислите
5 2 *2 2 =
Каким действием находится неизвестный член выражения
Х+9=36
Х-8=19
Х*4=100
6 2 /2 2
5 3 =
2 5 =
27 0 =
156 1 =
х/4=9
36 1/2 =
(3 2 ) 2 =
4 3 =
3 х =81
4 х =64
(2 3/4 ) 4 =
2 х =8
Вычислите
5 2 +3 2=
3 3 -2 3 =
Вычислите
5 2 *2 2 =
Каким действием находится неизвестный член выражения
Х+9=36
Х-8=19
Вычитанием
Сложением
Х*4=100
6 2 /2 2
5 3 =
2 5 =
27 0 =
156 1 =
Делением
х/4=9
Умножением
36 1/2 =
(3 2 ) 2 =
4 3 =
3 х =81
???
4 х =64
(2 3/4 ) 4 =
???
2 х =8
???
x
Используя графопостроитель Advanced Grapher показать графическое решение уравнения.
- Изучение понятия логарифма числа; знакомство с основным логарифмическим тождеством;
- Научиться применять определение логарифма и тождества к вычислениям и решению простейших логарифмических выражений.
Основное логарифмическое тождество
Вычислите
5 2 +3 2=
3 3 -2 3 =
Вычислите
5 2 *2 2 =
Каким действием находится неизвестный член выражения
Х+9=36
Х-8=19
Вычитанием
Сложением
Х*4=100
6 2 /2 2
5 3 =
2 5 =
27 0 =
156 1 =
Делением
х/4=9
Умножением
36 1/2 =
(3 2 ) 2 =
4 3 =
3 х =81
???
4 х =64
(2 3/4 ) 4 =
???
2 х =8
???
Предпосылки возникновения логарифмов:
Развитие в XVI в. производства и торговли, астрономии и мореплавания, требовали усовершенствования методов вычислительной математики. Требовалось производить громоздкие действия над многозначными числами с высокой точностью вычислений.
Ценность логарифмов:
сведение сложных действий возведения в степень и извлечения корня к более простым действиям умножению и делению, а их в свою очередь к самым простым — сложению и вычитанию.
Шотландский ученый Джон Непер (1550 - 1617) опубликовал сочинение "Описание удивительной
таблицы логарифмов", в котором кратко было
описано понятие логарифма, свойства.
Термин "логарифм", предложенный ученым,
прижился. Теория логарифмов была представлена
Непером в книге "Построение удивительной
таблицы логарифмов".
В 1617 году шотландский математик Генри Бригс (1561 - 1630) издал 14-значные таблицы десятичных логарифмов . Двумя годами позже лондонский учитель математики Джон Спайделл переиздал таблицы Непера, внеся в них исправления и дополнения.
Применение логарифмов:
- Свое применение и развитие теория логарифмов нашла в рекурсивных алгоритмах,
- теории фракталов,
- в теории чисел и математическом анализе,
- в статистике и теории вероятностей,
- информатике и вычислительной технике,
- механике и физике,
- химии,
- теории музыки,
- психологии и философии.
В природе логарифмические спирали встречаются на каждом шагу: растут раковины разнообразных моллюсков, рога у многих животных, во внутреннем ухе человека есть орган, называемый улитка, по спирали располагаются семена подсолнечника. По логарифмической спирали закручены и многие галактики, например галактика, которой принадлежит Солнечная система
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1850 руб.
2640 руб.
1460 руб.
2090 руб.
1650 руб.
2350 руб.
1750 руб.
2500 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
800 руб.
4000 руб.
500 руб.
2500 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства