Конспект урока геометрии в 9 классе

Геометрия, 9 класс

«Расположение прямой и плоскости, двух плоскостей в пространстве»

 

Цели урока:

• рассмотреть возможные случаи взаимного расположения прямых и плоскостей в пространстве; формировать навык чтения и построения чертежей, пространственных конфигураций, пространственных фигур к задачам.
• развивать пространственное воображение учащихся при решении геометрических задач, геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание; вырабатывать самостоятельность в освоении новых знаний.
• воспитывать у учащихся ответственное отношение к учебному труду, волевые качества;

формировать эмоциональную культуру и культуру общения,

развивать чувство патриотизма№

Тип урока: комбинированный.

Вид урока: урок смешанный

Методы обучения:

словесный, наглядный,  деятельностный

Формы обучения: коллективная, индивидуальная.

Оборудование: модели плоскости, куба,компьютер, интерактивная доска.

Технологии обучения: технология проблемно - развивающего обучения, информационно-коммуникационные  технологи,  технология интенсификации обучения на основе схемных и знаковых моделей.

План урока

1. Организационный момент.

2. Актуализация знаний.

3. Проверка раннее  усвоенных знаний (тест).

4. Подготовка учащихся к восприятию нового учебного материала.

5. Усвоение новых знаний.

6. Первичное осмысление  и закрепление знаний.

7. Закрепление изученного материала.

8. Обобщение и систематизация знаний и умений.

9. Подведение итогов.

10. Задание на дом.

 

Ход урока

 

«Наглядность –золотое правило дидактики»

 

1. Организационный момент.

 

Ребята, какой раздел геометрии мы начали изучать?

Назовите основные фигуры стереометрии.

Мы изучили с вами все возможности расположения прямых  в пространстве.

Как вы думаете, опираясь на наши знания в стереометрии ,мы готовы изучить взаимного расположения основных фигур в пространстве. (Прямой и плоскости). Верно. Поэтому тема нашего урока: «Расположение прямой и плоскости, двух плоскостей в пространстве». Сегодня на уроке мы должны рассмотреть с вами взаимное расположение прямой и плоскости, «открыть» определение параллельности прямой и плоскости, определение параллельных и пересекающихся плоскостей.

2. Актуализация знаний.

Учащимся задаются вопросы:

а) Сформулировать определение  параллельных прямых.

б) Сформулировать определение пересекающих прямых

с) Сформулировать определение скрещивающиеся прямые.

3. Проведение проверочного теста.

Применяя изученные знания из курса планиметрии о взаимном расположении прямых на плоскости, попытаемся решить вопрос о взаимном расположении прямых и плоскостей в пространстве.

 

Тест: Определите взаимное расположение прямых.

 

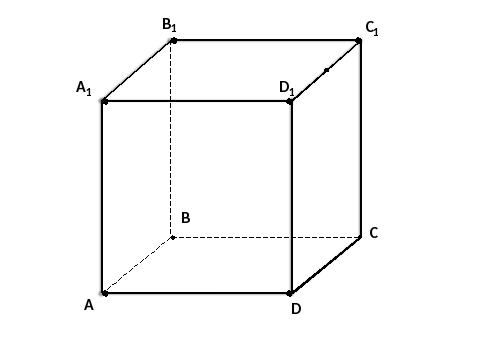
Дано:

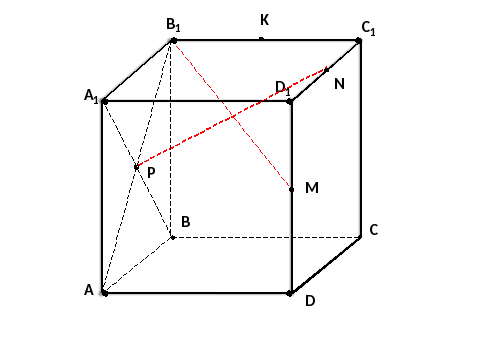
АВСДА1В1С1Д1- куб

Точки K, M, N - СЕРЕДИНЫ РЕБЕР

P - ТОЧКА ПЕРЕСЕЧЕНИЯ ДИАГОНАЛЕЙ ГРАНИ (А1В1В А.)

 

Рис.1

 

А)пересекаются; В) параллельные; С)скрещивающиеся; Д)перпендикулярные

Е) совпадают.

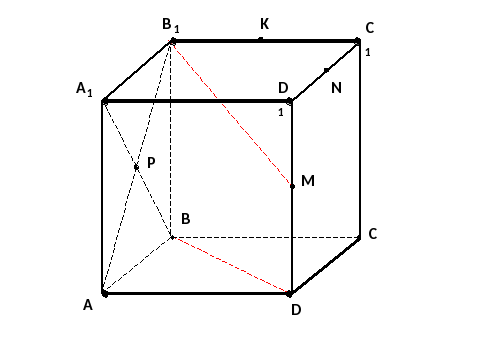
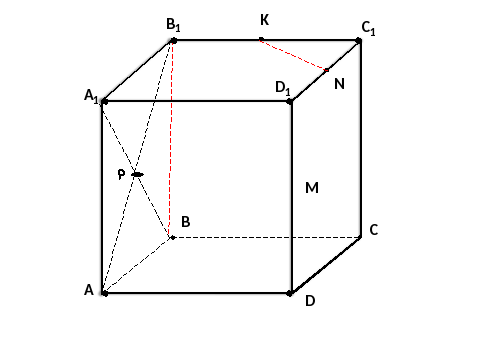
Рис 2

 

А)пересекаются; В) параллельные; С)скрещивающиеся; Д)перпендикулярные

Е) совпадают.

 

 

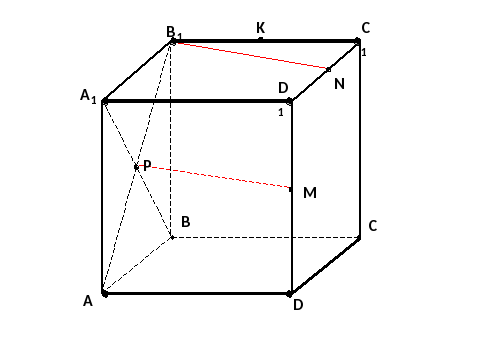
Рис 3

 

А)пересекаются; В) параллельные; С)скрещивающиеся; Д)перпендикулярные

Е) совпадают.

 

 

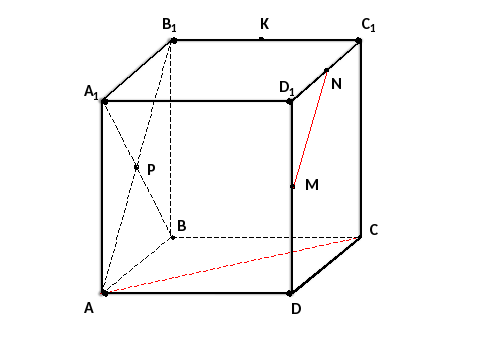
Рис4

 

 

А)пересекаются; В) параллельные; С)скрещивающиеся; Д)перпендикулярные

Е) совпадают.

 

Рис 5

 

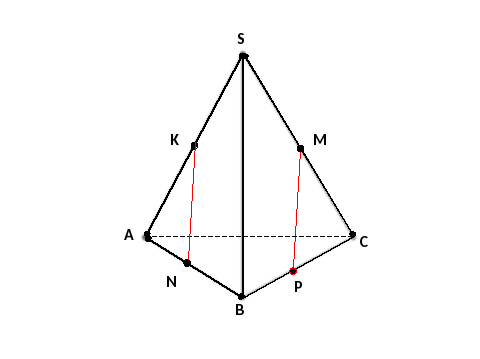
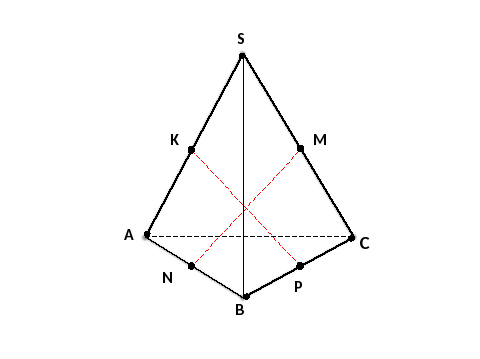
Дано: SАВС –тетраэдр, точки К, М,N,Р середины  ребер SА, SС, АВ, ВС,

Рис.6

 

 

А)пересекаются; В) параллельные; С)скрещивающиеся; Д)перпендикулярные

Е) совпадают.

 

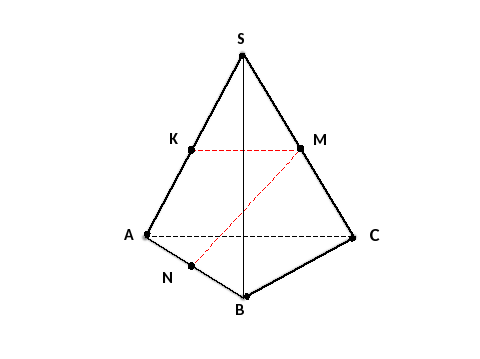
Рис.7

 

А)пересекаются; В) параллельные; С)скрещивающиеся; Д)перпендикулярные

Е) совпадают.

 

Рис.8

 

А)пересекаются; В) параллельные; С)скрещивающиеся; Д)перпендикулярные

Е) совпадают.

 

4. Подготовка учащихся к восприятию нового учебного материала

 

Ребята, как вы думаете,

• Какие существуют возможности взаимного расположения прямой и плоскости?
• Сколько общих точек у прямой и плоскости в каждой из возможностей?
• Приведите примеры из окружающего нас мира, иллюстрирующие эти возможности.
• Сколько общих точек у прямой и плоскости в каждой из возможностей?
• Приведите примеры из окружающего нас мира, иллюстрирующие эти возможности.

5. Усвоение новых знаний.

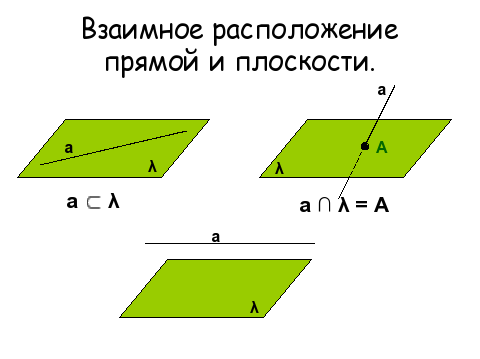
 Взаимное расположение прямой и плоскости:

Прямая принадлежит данной плоскости.

 

 

 

 

Определение:

Прямая называется параллельной плоскости, если она не имеет с этой плоскостью общих точек.

 

 

 

 

Определение:

Прямая и плоскость называется пересекающимися, если они имеют одну общую точку.

 

 

 

 

 

 

 

 

 

 

 

 

 

Прямая перпендикулярная плоскости.

                                                      d

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

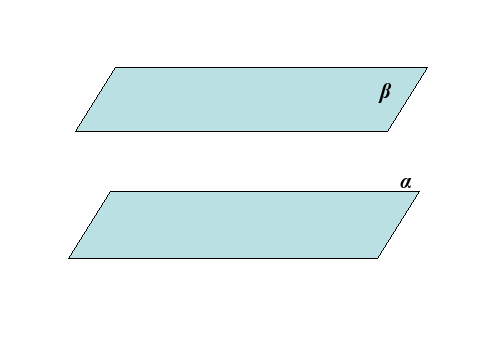
Взаимное расположение плоскостей

 

Определение: плоскости называются параллельными ,если они не имеют

общих точек.

 

 

 

 

Определение: Две плоскости называются пересекающимися, если они имеют общую точку.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Первичное осмысление и закрепление новых знаний.

В классной комнате, используя признак параллельности прямой и плоскости, укажите прямые и параллельные им плоскости.

 

6. Упражнения на закрепление изученного материала (устная работа)

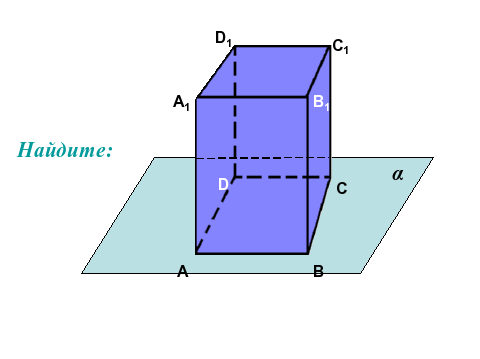
Рис.1

 

 

Несколько точек, которые лежат в плоскости α.

Ответ: точки: А,В,С,Д.

 

Рис.2

 

Несколько точек, не лежащих в плоскости α.

Ответ: точки А1,Д1,С1,В1.

 

 

 

 

 

 

Рис.3

 

Несколько прямых, которые лежат в плоскости α

Ответ:4 прямые( ДС,СВ,АД,АВ.)

Рис.4

 

Несколько прямых не принадлежащих плоскости α

  4 прямые

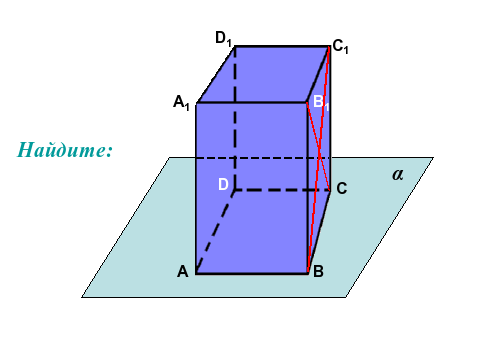
Рис 5

 

Несколько прямых, которые пересекают прямую ВС.

Ответ:С1В, ДС,АВ..)

 

Рис 6

 

Назовите:

1.прямые пересечения плоскости  α и грани (АА1Д1Д)

2.Назовите параллельные плоскости.

Ответ: 1) прямая АД.

            2) плоскости α и грани А1В1С1Д1.

6. Упражнения на закрепление изученного материала

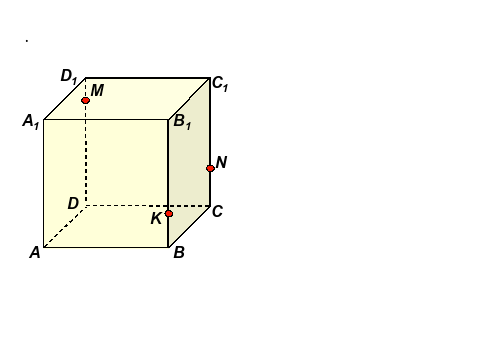
Задача: Дан куб АВСДА1В1С1Д1,

Точка М лежит на ребре ДД1;

Точка N лежит на ребре СС1;

Точка К лежит на ребре ВВ1.

 

1. Назовите плоскости в которых лежат  точки М и N.

2. Назовите прямые перпендикулярные плоскости граниА1В1С1Д1

3.Найдите прямые пересечения плоскости (ДМN) и  грани( АВСД)

4.Определите взаимное расположение  плоскостей (АА1К) и грани (ДД1С1С).

 

Ответ:1) АДА1Д1, Д1С1СД.

             2) АА1,ВВ1, СС1,ДД1.

             3) прямая ДС.

              4) плоскости параллельны.

Решение задач с использованием интерактивной доски.

№268, 270, (271)

 

Задача 1: Начертите куб

Назовите:

1) вне плоскости, параллельные прямой, проходящей через ребро АА,

2) вне плоскости,параллельные прямой, проходящей через ребро СД.

3) все прямые, параллельные плоскости АВСД.

На чертеже куба

 

 

 

М

 

 

 

 

 

 

 

 

М1                                          Q1

Назовите:

1) плоскости, пересекающиеся с прямой, проходящей через ребро РР1.

2) плоскости, пересекающиеся с прямой, проходящей через ребро NQ

3) все прямые, пересекающие плоскость ММ1N1N

 

7. Обобщение и систематизация знаний и умений

 

1. Что означает: прямая и плоскость параллельны?
2. Какие плоскости называются параллельными?
3. Прямые а и с параллельны, прямые в и а пересекаются.

Могут ли прямые в и с  пересекаться?

1. Прямая а пересекает плоскость β. Лежит ли в плоскости β хоть одна прямая, параллельная прямой а?

 

8. Подведение итогов урока.

 

9. Постановка домашнего задания. П.16, задачи №267,266.

 

Урок окончен, спасибо, вам, за урок, ребята.