КГУ «общеобразовательная средняя школа-гимназия №1 имени Н.А.Островского»
Города Шемонаихи Шемонаихинского района Восточно-Казахстанской области
Урок алгебры в 9 классе
Учитель математики первой категории
Матвеева Светлана Борисовна
Г.Шемонаиха,ВКО
Цели урока:
Обобщить понятие арифметической и геометрической прогрессии, повторить формулы ,применение знаний при решении заданий ВОУД и ЕНТ.
Закрепление понятий «прогрессия», «член прогрессии», «разность», «знаменатель», «сумма».
3. Отработать умения и навыки применения формул n-го члена прогрессии, суммы n - первых членов, свойств членов прогрессии.
Задачи:
обобщить и закрепить теоретические знания учащихся;
развивать умения и навыки применять формулы прогрессий при решении задач;
повысить интерес к предмету, расширить кругозор по данной теме.
Тип урока: урок закрепления материала.
Оборудование урока ИД, презентация.
Ход урока:
В начале урока приветствие ребят и учителя.
«Тему сегодняшнего урока мы узнаем, разгадав кроссворд:»
1. Как называется график квадратичной функции?
2. Математическое предложение, справедливость которого доказывается.
3. Упорядоченная пара чисел, задающая положение точки на плоскости.
4. Наука, возникшая в глубокой древности в Вавилоне и Египте, а учащиеся начинают её изучать с 7 класса.
5. Линия на плоскости, задаваемая уравнением у=кх+b.
6. Числовой промежуток.
7. Предложение, принимаемое без доказательства.
8. Результат сложения
9. Название второй координаты на плоскости.
10. Французский математик 19 века, «отец» алгебры, юрист, разгадал шифр,
применяемый испанцами в войне с французами, а нам помог в быстром
решении квадратных уравнений.
Итак, тема урока «Прогрессии».
2.Постановка цели урока.
3.Закрепление материла:
1.Определение арифметической прогрессии.
2.Что называют разностью арифметической прогрессии? Как обозначают?
3.Формула n-ого члена арифметической прогрессии.
4.В чем заключается свойство арифметической прогрессии?
5.Назовите формулу суммы n-первых членов арифметической прогрессии.
Какие из последовательностей являются арифметическими прогрессиями?
3, 6, 9, 12,…..
5, 12, 18, 24, 30,…..
7, 14, 28, 35, 49,….
5, 15, 25,….,95….
1000, 1001, 1002, 1003,….
1, 2, 4, 7, 9, 11…..
5, 4, 3, 2, 1, 0, -1, -2,….
Найти разность арифметической прогрессии:
1; 5; 9………
105; 100….
-13; -15; -17……
11; а2; 19,….
1.Определение геометрической прогрессии.
2.Что называют знаменателем геометрической прогрессии? Как обозначают?
3.Формула n-ого члена геометрической прогрессии.
4.В чем заключается свойство геометрической прогрессии?
5.Назовите формулу суммы n-первых членов геометрической прогрессии.
Какие из последовательностей являются геометрическими прогрессиями?
2, 6,18,…..
15, 22, 28, 35, 49,…..
7, 14, 28, 35, 49,….
5, 15, 45,….
10, 100, 1000, 10000,….
1, 2, 4, 7, 9, 11…..
125,25,5,1,….
Найти знаменатель геометрической прогрессии:
1; 3; 9………
100; 10….
-13;26; -52……
11; в2 ; 44,….
Между числами 6 и 21 вставьте 4 числа так, чтобы вместе с данными числами они образовали арифметическую прогрессию.
Решение: а1 = 6, а6 = 21,
d = (21 – 6)/ (6 – 1)= 3,
6, 9, 12, 15, 18, 21.
Класс делится на 2 группы, одна группа проходит в кабинет информатики для прохождения тестирования (приложение )по данной теме, вторая работает в классе по плану, через 15 минут группы меняются местами.
Дана “стайка девяти чисел”:
3, 5, 7, 9, 11, 13, 15,17, 19.
Она представляет собой арифметическую прогрессию. Кроме того, данная стайка чисел привлекательна способностью разместиться в девяти клетках квадрата 3х3 так, что образуется магический квадрат с константой, равной 33.
Знаете ли вы, что такое магический квадрат? Квадрат, состоящий из 9 клеток, в него вписывают числа, так чтобы сумма чисел по вертикали, горизонтали диагонали была одним и тем же числом- constanta.
Замечание об арифметической прогрессии само по себе очень интересно. Дело в том, что из каждых девяти последовательных членов любой арифметической прогрессии натуральных чисел можно составить магический квадрат.
1) а1 = 5, d = 3, а7 - ? 23
2) а4 = 11, d = - 2, а1-? 17
3) а4 = 12,5, а6 = 17,5 а5 - ? 15
4) а1 = -3, а2 = 4, а16 - ? 102
5) а1 = 4, а7 = -8, d -? -2
6) а7 = -5, а32 = 70, а1 - ? -23
7) 2, 5, 8,… S11 - ? 187
8) b1 = 5, q = 3,b4 - ? 135
9) b4 = 16, q = - 2, b1-? -2
10) b4 = 12,5, b6 = 48 b5 - ? 24
11) b1 = -3, b2 = 4, b6 - ? 96
12) 2, 8,32… S5 - ? 682
Задача «Наследство».
Джентльмен получил наследство. Первый месяц он истратил 1000$, а каждый следующий месяц он тратил на 500$ больше, чем в предыдущий. Сколько $ он истратил за второй месяц? За третий? Каков размер наследства, если денег хватило на год такой безбедной жизни?
Решение:
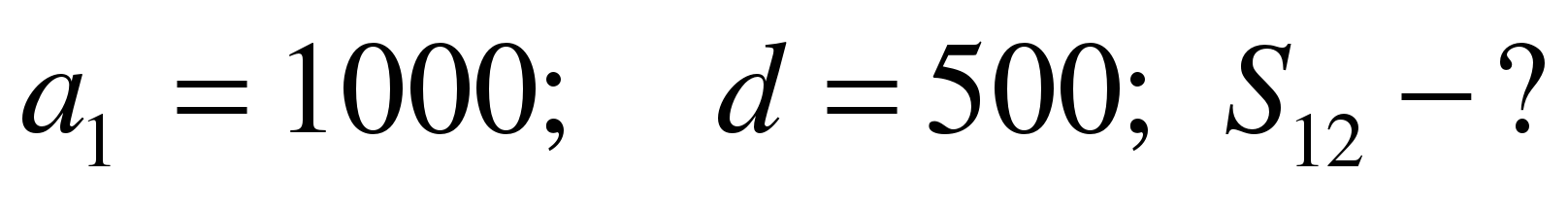
Применив формулу 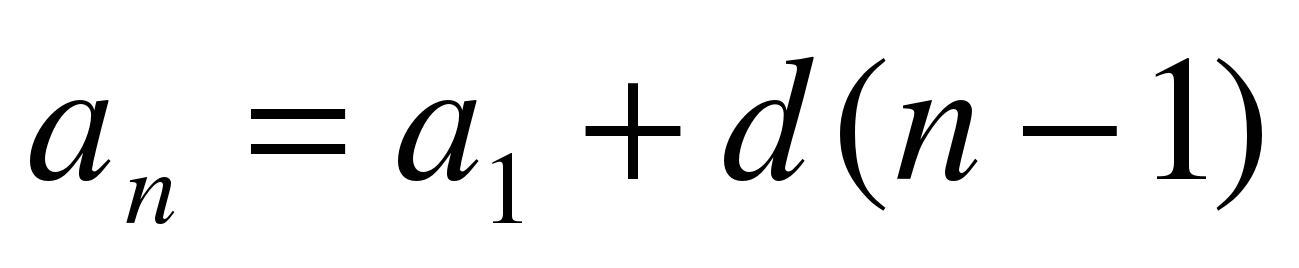 , получаем:
, получаем:
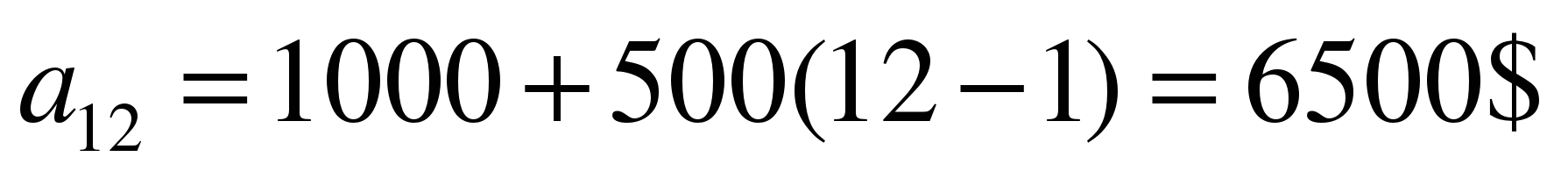
Применив формулу: 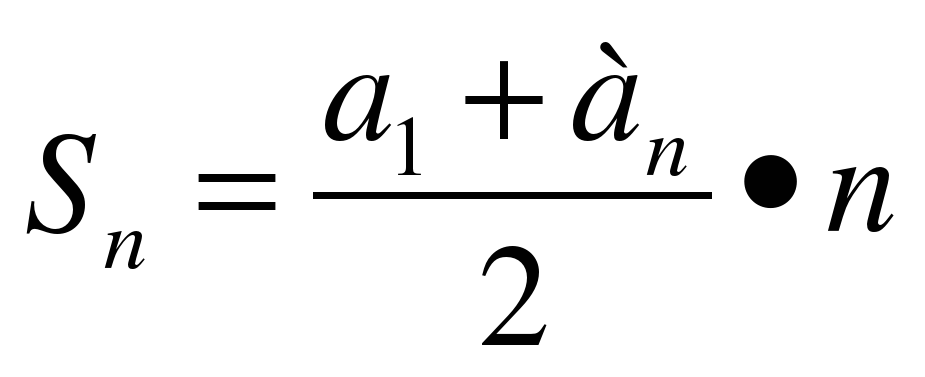 , получим:
, получим:
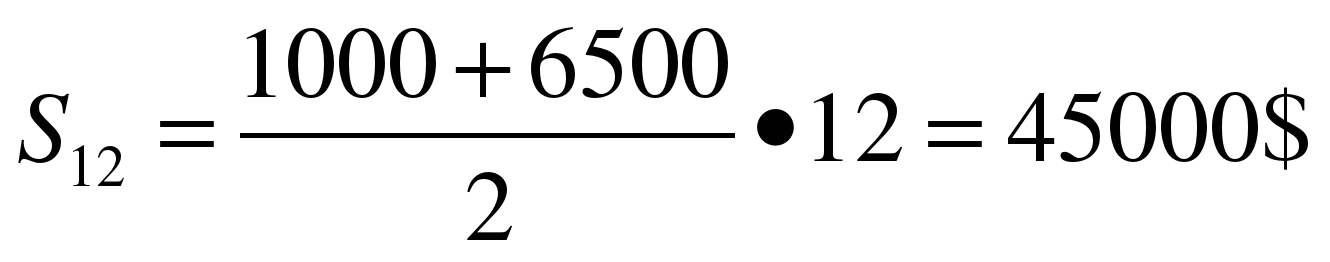
4.Итог урока.
Домашнее задание:
Составить тест на 10 вопросов по теме «Арифметическая прогрессия» первый вариант и «Геометрическая прогрессия» второй вариант.
И вспомним начало нашего урока, ребята. А какие цели урока мы ставили перед собой?
Как Вы считаете, нам удалось достигнуть поставленных целей?
| «Ребята, а теперь сами оцените свою работу на уроке. Перед вами карточка с изображением горы. Если вы считаете, что хорошо усвоили на уроке, разобрались в понятии арифметической прогрессии, то нарисуйте себя на вершине горы. Если осталось что-то неясно, нарисуйте себя ниже, а слева или справа решите сами. Передайте мне свои рисунки. |
|
Спасибо за урок, ребята. Мне кажется, что Вы сегодня хорошо потрудились».
ПРИЛОЖЕНИЕ
Задания взяты из сборников для пробного тестирования ЕНТ
1. Найдите пятый член геометрической прогрессии, если b1= 6, b3 =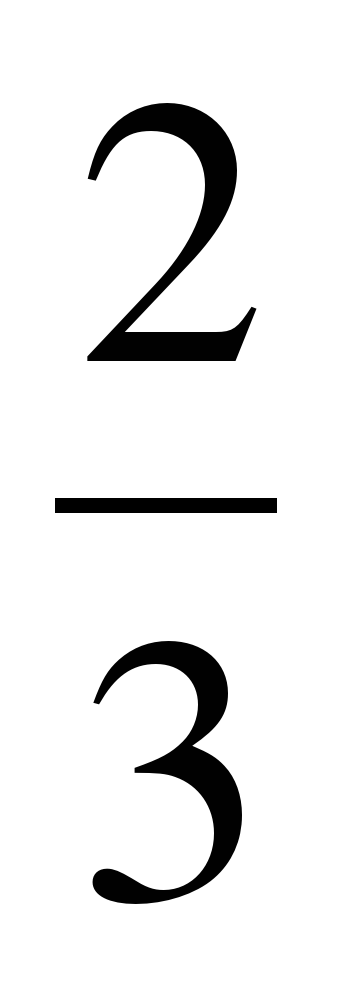
A) 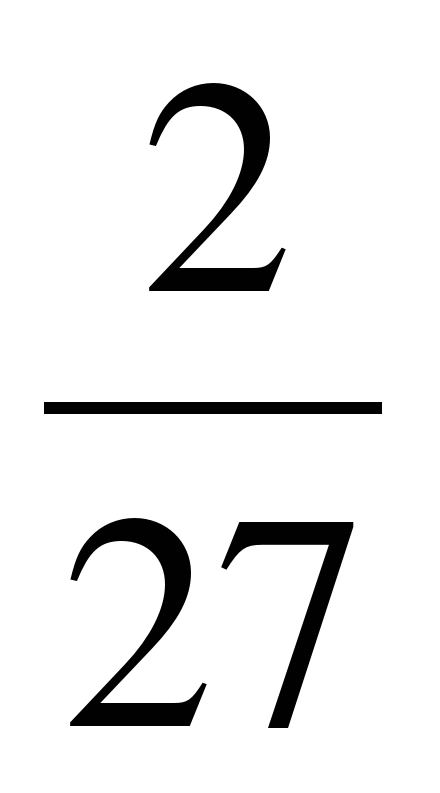 B)
B) 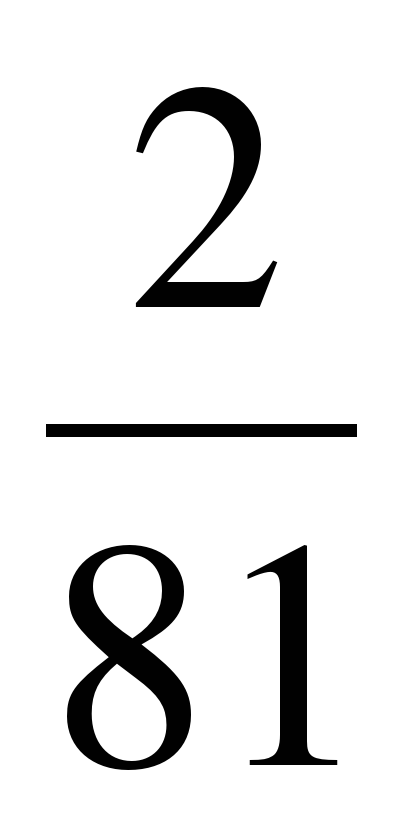 C)
C) 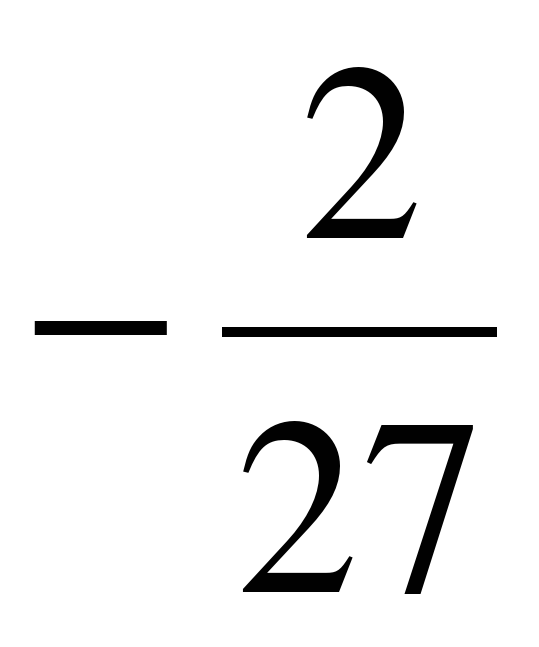 D)
D) 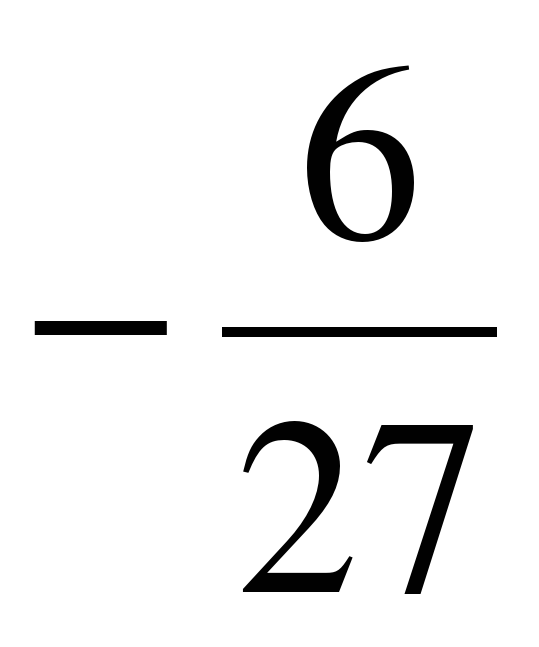 E)
E) 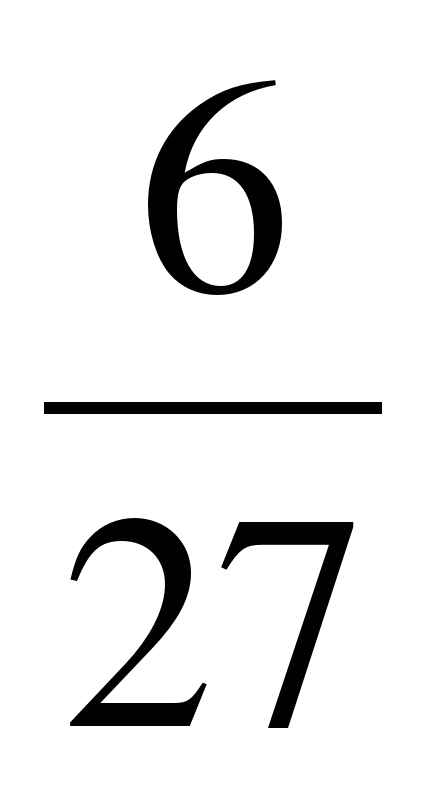
2. Найдите сумму пяти первых членов геометрической прогрессии ,если
в1=324 ,q= � �
�
-484 ; B) -324 ; C)243 ; D)484 ; E) -243
3.Последовательность, заданная формулой an=4n+3 является арифметической прогрессией. Найдите сумму её первых тридцати членов
390 ; B) 421 ; C)394 ; D)413 ; E) 403
4.Найдите пятый член геометрической прогрессии, в которой
b3+b4=36; b3+b2=18
72 ; B) 48 ; C)54 ; D)24 ; E) 96
5. Определить число членов геометрической прогрессии, если известно, что b3 - b1=8 ; b6 - b4=216 ;Sn=121
8 ; B) 7 ; C)4 ; D)5 ; E) 6
6.Найдите сумму восьми первых членов геометрической прогрессии ,если
в1=1024 ,q= � �
�
2100 ; B) 1020 ; C)2040 ; D)2048 ; E)2041
7.В геометрической прогрессии в1=�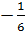 �, в2=�
�, в2=� �.Найдите пятый член этой прогрессии
�.Найдите пятый член этой прогрессии
�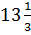 � ; B) 40,5 ; C)-13,5; D)�
� ; B) 40,5 ; C)-13,5; D)�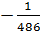 � ; E) �
� ; E) �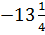 �
�
8.В геометрической прогрессии в1=125�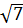 �, в3=5�
�, в3=5�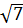 �.Найдите знаменатель q этой прогрессии
�.Найдите знаменатель q этой прогрессии
�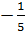 � ; 5 ; B) �
� ; 5 ; B) � � ; 5; C)-5; D)5 ; E) +5
� ; 5; C)-5; D)5 ; E) +5
9.Частное от деления четвёртого члена геометрической прогрессии на её первый член равно 64 ,третий член прогрессии равен 8. Найдите первый член прогрессии
� � ; B) �
� ; B) �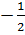 � ; C)-2; D)4 ; E) 2
� ; C)-2; D)4 ; E) 2
10.Найдите сумму десяти первых членов арифметической прогрессии ,если а5 =9; а9+а2=20
А)110 ; B) 101 ; C)100 ; D)99 ; E)90
















