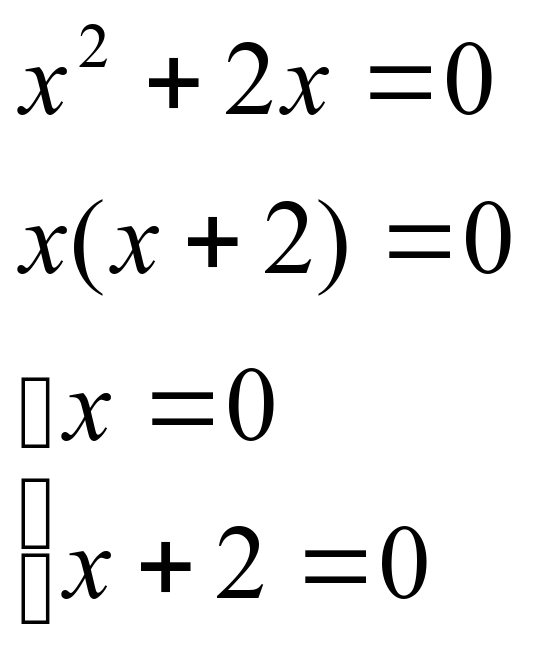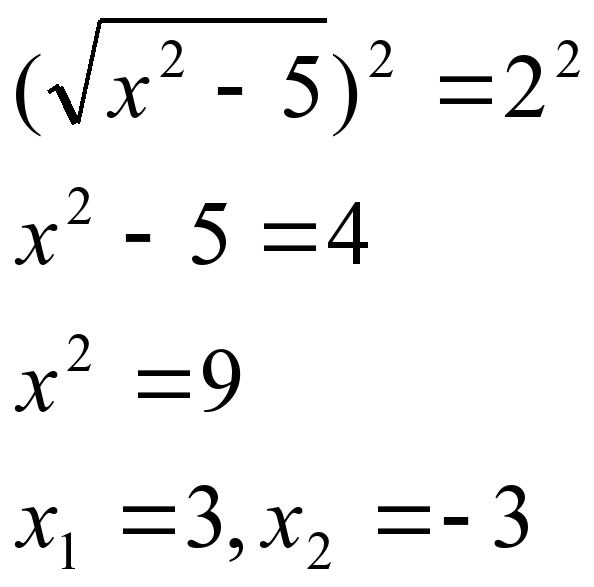Конспект хорош для подготовки учащихся 9-х классов к ГИА. Тема: Решение уравнений. Цель: систематизировать теоретические и практические знания учащихся 9-х классов по решению биквадратных, дробно-рациональных и иррациональных уравнений. Планируемые результаты обучения. К концу урока учащиеся: 1) вспомнят методы решения биквадратных, дробно-рациональных и иррациональных уравнений; 2) научатся решить биквадратное, дробно-рациональное и иррациональные уравнения стандартного уровня; 3) получат возможность научиться решать биквадратное, дробно-рациональное, иррациональные уравнения повышенного уровня.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Конспект урока алгебры по теме "Решение уравнений"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Конспект урока алгебры по теме "Решение уравнений" »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1690 руб.
2820 руб.
1720 руб.
2860 руб.
1800 руб.
3000 руб.
1430 руб.
2380 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
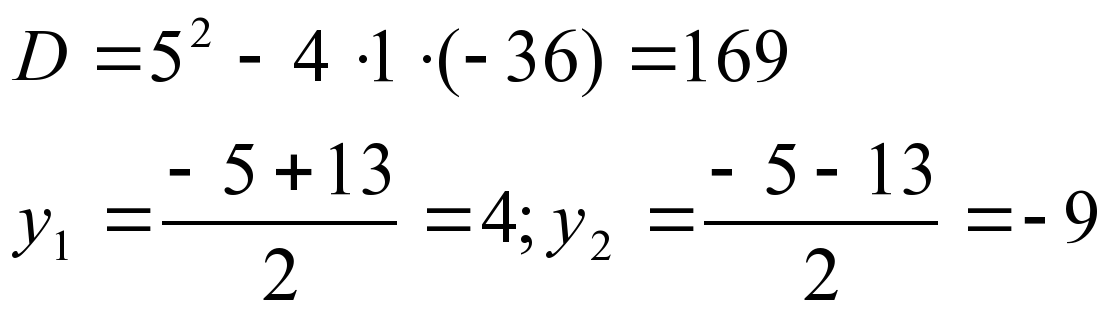
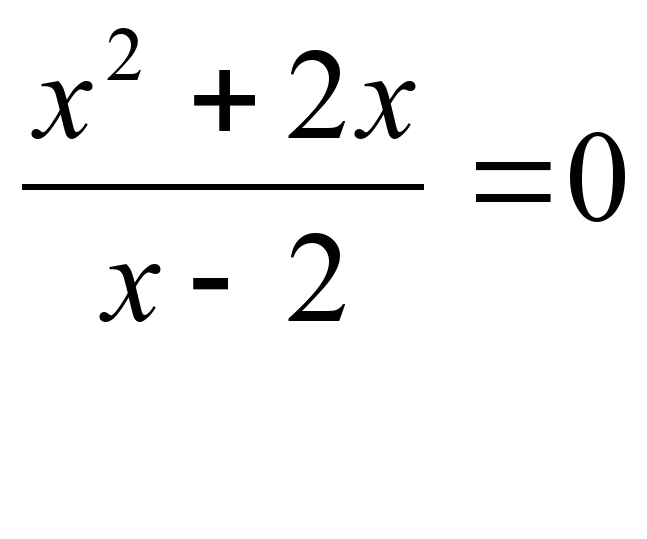 О.Д.З.
О.Д.З.