Интегрированный урок по теме: "Решение задач на растворы и сплавы"

Данные об учителе: Бруяка Оксана Дмитриевна

Предмет

Алгебра (УМК линия Мордкович А.Г.)

Класс

8

Тема урока

Решение задач на растворы и смеси .

Планируемые образовательные результаты:

Применять понятия и определения математики в решении задач по химии на растворы и смеси из реальной жизни.

Предметные

Метапредметные

Личностные

Научится: Оперировать понятиями раствор, растворитель, концентрация, процент, массовая доля, нахождение процента от числа, нахождение числа по его части, строить логическую цепочку рассуждений, сопоставлять полученный результат с условием задачи.

Доказывать и опровергать с помощью контр примеров утверждения

Ученик получит возможность повторить и откорректировать знания по теме: «Решение задач на растворы и смеси»:

Углубить и развить представления о решении задач на растворы и смеси.

Исследовать новые простейшие, необычные представления о числовых закономерностях в решении задач.

Познавательные:

- Выдвижение гипотез и их обоснование;

- Умение составлять схемы и уравнения к текстовым задачам.

- Поиск и выделение необходимой информации;

Регулятивные: Коррекция; Целеполагание

Коммуникативные: Эффективно сотрудничать и способствовать продуктивной кооперации

- Развитие логического мышления, внимания;

-Развитие математической и химической речи;

-Развитие интереса к предметам;

- Умение контролировать процесс и результат учебной математической деятельности;

Решаемые учебные проблемы

Осмысленное решение химических задач на уроке математики. Поиск более простого решения задач. Применение знаний в реальной жизни.

Основные понятия, изучаемые на уроке

раствор, растворитель, концентрация, процент, массовая доля, нахождение процента от числа, нахождение числа по его части, построение логической цепочки рассуждений, сопоставление полученного результата с условием задачи.

Вид, используемых на уроке средств ИКТ

Презентация

Методическое назначение средств ИКТ

Активизация познавательного процесса на уроке

Аппаратное и программное обеспечение

Мультимедийный проектор, компьютер, раздаточный материал

Образовательные Интернет-ресурсы

ОРГАНИЗАЦИОННАЯ СТРУКТУРА УРОКА

1. Структура интегрированного урока (по ФГОС)

ЭТАП 1. Организационный этап

Формирование конкретного образовательного результата (группы результатов)

Дли-тель

ность этапа

Основной вид учебной деятельности, направленной на формирование данного образовательного результата

Методы обучения

Средства ИКТ для реализации данного вида учебной деятельно-сти

Форма организации деятельности учащихся

Функции (роль учителя на данном этапе)

Основные виды деятельности учителя

Личностные: Нравственно-этическое оценивание исходя из социальных и личностных ценностей

2 мин.

Эмоциональный настрой и познавательный интерес к теме. Быстрое включение учащихся в деловой режим.

Работа с высказыванием:

Н.И. Лобачевский «Математика – это язык, на котором говорят все точные науки».

М.В. Ломоносов «Далеко простирает химия руки свои в дела человеческие»

Презентация,

Просмотр слайда и диалог с учителем.

проблемного характера: эмоционально настроить учащихся на интегрированный урок.

Проводит диалог с учащимися

учитель по высказыванию Н.И. Лобачевского;

М.В. Ломоносова

ЭТАП 2. Вхождение в тему урока и создание условий для осознанного восприятия нового материала

П- Поиск и выделение необходимой информации

К- оценка действий партнёра умение с достаточной полнотой и точностью выражать свои мысли

5 мин.

Установить правильность, осознанность усвоения учащимися типов текстовых задач

Диалог

Отвечают на вопрос учителя: 1. Какие типы текстовых задач решаем в школьном курсе математики?

2.Какой тип задач более связан с химией?

3.Какие слова навели вас на правильный ответ?

Организовать самопроверку

Учитель: Использование небольшой психологической паузы и вопроса: Какой тип задач более связан с химией?

побуждающего внимание учащихся к теме урока.

ЭТАП 3. Актуализация знаний. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

П- самостоятельное выделение и формулирование познавательной цели

Р- Целеполагание

5 мин.

1.Осмысленное восприятие информации

2.Формулировка темы и целей урока.

Практическая «разминка»

вопросы для «разминки».

1.Отвечают на вопросы. Выполняют задания, сообщают о результатах.

2.Делятся мнениями на поставленную проблему.

3.Выдвигают гипотезу.

4.Формулируют тему урока и цель урока.

Подвести ответы детей к проблеме: Решали или нет такого типа задачи на уроках химии и математики? И что же предстоит сделать на этом уроке? Актуальность этих задач?

Помогает сформулировать тему урока

1. Учитель даёт задания устного счёта на проценты.

ЭТАП 4. Применение знаний решения задач на растворы в реальной жизни.

П- самостоятельное выделение и формулирование познавательной цели

Л- Развитие математической и химической речи;

Р- Целеполагание

К- оценка действий партнёра умение с достаточной полнотой и точностью выражать свои мысли

10

мин

Текстовая постановка проблемных задач из реальной жизни.

Работа с химическими понятиями.

.1.Делятся мнениями на поставленную проблему.

2.Работают с химическими определениями и понятиями.

Настроить детей на применение методов решения задач

Учитель : Организация работы у доски по карточкам-заданиям.

ЭТАП 5. Организация и самоорганизация учащихся в ходе дальнейшего обобщения и систематизации знаний материала. Практикум.

П-Выбор эффективных способов решения задач

П-Извлечение необходимой информации из прослушанных, прочитанных текстов различных задач

К- оценка действий партнёра умение с достаточной полнотой и точностью выражать свои мысли

10 мин

1.Выполнение задачи №1 (на растворы ) по карточкам в тетрадях и у доски.

2, Защита приёмов решения задачи.

Работа с текстом ,

представление основного материала одновременно в словесной, знаково-символической форме и в виде таблицы

1.Выполняют задание №1 письменно.

2.Делятся мнениями на поставленную проблему.

3.Работают с определением молярной массы и концентрации.

4.Делают выводы в выборе метода решения, в выборе схемы решения, учитывая знание формул по химии и химических обозначений.

Создание условий для освоения учащимися знаний преимущественно в форме деятельности

Учитель:

1.Руководит последователь

ностью защиты методов решения задачи.

2. Предлагает сделать

выводы.

3.Организует обсуждение результатов.

.

ЭТАП 6. Новое, давно забытое старое. Или арифметический способ решения задач на растворы.

П-Выбор эффективных способов решения задач

Умение составлять схемы и уравнения к текстовым задачам.

Р- Коррекция; Целеполагание

Л - Развитие интереса к предметам;

5мин

1.Выполнение задач арифметическим методом.

Работа со схемой и самостоятельное составление схемы и решение задачи.

1.Работают в парах.

2.Делают выводы в выборе решения.

Создание условий для освоения учащимися знаний преимущественно в форме деятельности.

Предлагает сделать

выводы.

Организует обсуждение результатов.

Руководит работой на местах.

ЭТАП 7. Первичная проверка полученных результатов. Коррекция.

Длительность этапа

Виды учебной деятельности для проверки полученных образовательных результатов

Средства ИКТ для реализации данного вида учебной деятельности

Методы контроля

Способы коррекции

Форма организации деятельности учащихся

Функции(роль учителя на данном этапе)

Основные виды деятельности учителя

3-5мин.

Выполнение по карточкам: 1 вариант: задача №3;

2 вариант: задача №4.

Слайд с текстом

проверка выполнения в тетради

Комментарии

учеников и учителя к решению на слайде

Работа с карточками-заданиями

Настраивает детей на быстрое выполнение задания

Помогает комментировать

задания после проверки тетрадей.

ЭТАП 8. Информация о домашнем задании, инструктаж по его выполнению.

Образовательные задачи этапа учебного занятия

Содержание этапа учебного занятия

Показатели выполнения образовательных задач этапа

Условия выполнения образовательных задач этапа

Возможный метод и приём обучения

Обеспечить понимание учащихся цели содержания и способов выполнения домашнего задания.

1.информация о домашнем задании

2.инструктаж по выполнению д/з.

находить необходимую для выполнения работы инфор­мацию в материалах учебника

Соответствие содержания д/з уровню обученности учащихся.

Запись домашнего задания в дневник

Задание:

1 уровень: на карточках две задачи

2уровень: на карточках две задачи

ЭТАП 9. Рефлексия (Подведение итогов занятия)

Образовательные задачи этапа учебного занятия

Содержание этапа учебного занятия

Показатели выполнения образовательных задач этапа

Условия выполнения образовательных задач этапа

Возможный метод и приём обучения

1.Дать качественную оценку работы класса

2.Инициировать рефлексию учащихся по поводу своего эмоционального состояния, мотивации своей деятельности и взаимодействия с учителями и одноклассниками

1.Подведение итогов урока

2.Мобилизация учащихся на рефлексию своего поведения

1.Чёткость и краткость

2.Открытость учащихся в осмыслении своих действий и самооценке

Умение учителя давать качественную характеристику работы класса

Развитие способностей учащихся к рефлексии

Приём «Смайлики»:

Суть- зафиксировать свои достижения на уроке:

Я разобрался в теме…

Я пропускаю ход…

Сокращения в технологической карте: П- познавательные УУД; К- коммуникативные; Р- регулятивные; Л-личностные

Ход урока:

Этапы урока

Деятельность

учителя

ученика

ЭТАП 1.

Организационный этап

Здравствуйте, дети.

Я рада вас видеть.

Кто сегодня дежурный? Назовите отсутствующих. Сегодняшнее число? (учитель записывает число на доске). Совершенно верно.

Итак, начинаем наш урок.

Сегодня у нас не совсем обычный урок, у нас интегрированный урок по решению задач на растворы. Просим вас по ходу урока активно работать.

Эпиграфом к уроку мы взяли слова:

Н.И. Лобачевского «Математика – это язык, на котором говорят все точные науки» Ну а М.В. Ломоносов - «Далеко простирает химия руки свои в дела человеческие» (говорит учитель математики)

1.Приветствуют учителя. Готовятся к уроку:

в тетрадях записывают число и классная

работа.

2.Смотрят

на слайд презентации.

3.Отвечают

на вопрос учителя.

ЭТАП 2.

Вхождение в тему урока и создание условий для осознанного восприятия нового материала

Учитель: В курсе школьной математики изучают различные практические, текстовые задачи. Давайте вспомним их и кто мне подскажет типы этих задач? (ведётся диалог).

Задачи на числа

Задачи на движение

Задачи на работу

Задачи на растворы, смеси и сплавы

Скажите: какой тип задач более связан с химией? (Высказывания детей)

Да! Ближе всех к химии задачи на растворы, смеси и сплавы. Какие слова навели вас на правильный ответ? (ответы детей).

Когда мы решаем такие задачи на уроке математики, то нам не хватает химического обоснования этих задач.

1.Ученики отвечают на вопросы учителя:

1. Какие типы текстовых задач решаем в школьном курсе математики?

2.Какой тип задач более связан с химией?

3.Какие слова навели вас на правильный ответ?

ЭТАП 3. Актуализация знаний. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

Учитель : Давайте мы с вами подумаем и сформулируем цель урока: чем же сегодня будем заниматься на уроке математики? (Учитель подводит ответы детей к проблеме: Решали или нет такого типа задачи на уроках химии и математики? И что же предстоит сделать на этом уроке? Актуальны ли эти задачи? Учитель помогает сформулировать тему и цель урока).

Итак, мы пришли к цели урока:

- Вспомним, обобщим, свяжем решение задач на растворы, сплавы и смеси с химическими понятиями и, конечно же, будем искать более простое и оригинальное решение.

А нужно ли нам это? Актуальны ли эти задачи? Для чего же нужно уметь решать такие задачи? (Учитель подводит диалог с учащимися к ответам:

- Для успешной сдачи ОГЭ и по химии и по математике.

- Для дальнейшей нашей жизни и деятельности.).

Запишем тему урока: Систематизация и обобщение знаний по решению задач на растворы и смеси (учитель записывает тему на доске).

А для старта нам необходима небольшая «разминка» (проводится устный счёт по теме «Проценты»):

Посмотрите на слайд, и проведём небольшой устный счёт.

(Понятие «процент». Предоставлены примеры на темы: Перевод процентов в десятичную дробь и десятичной дроби в проценты. Как найти процент от числа? Как найти число по его части?).

1.Отвечают на вопросы учителя

. 2.Делятся мнениями на поставленную проблему.

3.Выдвигают гипотезу.

4.Формулируют с помощью учителя тему урока и цель урока.

ЭТАП 4. Применение знаний решения задач на растворы в реальной жизни.

Учитель : Размялись, а теперь за задачи на растворы:

К доске пойдут Грищенко Катя ,Потовский Владислав , Семененко Катя .(Всем троим предстоит решить одну и ту же задачу, но только применяя указанный на листочке метод. Эта задача №1 из раздаточного материала к уроку, которая есть у каждого ученика на его столе. Учитель контролирует решение и оформление решения на доске).А также обращается к ученикам со следующими вопросами:

У нас дома есть скутер и машина. И мне часто приходится слышать об аккумуляторах и электролите. Что это такое? В чём могут быть проблемы? Как их решить? И нужно ли мне это знать?

Ответ: (в виде диалога учителя с учениками). Конечно, всё готовое в наше время можно купить в специализированных магазинах, но знать, с чем имеешь дело, должен каждый. Бывают моменты, когда магазина рядом нет, а проблема есть и необходимо её решить.

- Кто знает: Что такое электролит?

- Электролит - это раствор солей, щелочей и кислот.

- Что такое кислотный электролит?

- Раствор концентрированной серной кислоты H2SO4 в дистиллированной воде H 2O.

- Для чего он используется?

- Электролит в аккумуляторе является средой, в которой происходят химические реакции, позволяющие накапливать электрическую энергию и отдавать её.

Саша, ты понял, что такое электролит? А как приготовить электролит, ты узнаешь подробнее на уроке химии . А в следующей задаче указана одна из проблем, которая может возникнуть с аккумулятором. Эта проблема представлена в задаче.

Задача: Приготовить 980 граммов кислотного электролита для аккумулятора, имея 98% раствор серной кислоты H2SO4 . Сколько нужно взять воды H2O и серной кислоты H2SO4, чтобы получить 37%-ный раствор электролита?

Теперь послушаем Катю.

Катя: А меня интересует, как решить вот такую задачу:

Как из 78%-ной уксусной эссенции в домашних условиях приготовить 9%-ный уксус. И для чего в заготовках на зиму используют уксус?

Ответ: (в виде диалога: учитель и ученики)

Учитель математики: Задачи-проблемы Саши и Кати мы увидели. Как видите это задачи из нашей повседневной жизни. Но решать мы их сейчас не будем. В конце урока вы сами сможете помочь им решить их задачи, применяя выбранный вами способ решения.

1.Делятся мнениями на поставленную проблему.

2.Работают с химическими определениями и понятиями.

3.Отвечают у доски по заданиям.

ЭТАП 5. Организация и самоорганизация учащихся в ходе дальнейшего обобщения и систематизации знаний материала. Практикум.

Учитель: А сейчас рассмотрим алгоритмы решения задач, в которых фигурируют растворы.

Ученики-консультанты по химии и математике подготовили нам решение задачи №1, которая есть на каждом столе. Вначале мы с вами ознакомимся с текстом. (Читает вслух один из учеников)

Задача №1: Смешали 30%-ный раствор соляной кислоты с 10%-ным раствором и получили 600г 15%-ного раствора. Сколько граммов каждого раствора было взято?

Решение задачи №1:

Алгебраический способ (слово предоставлено ученикам у доски):

(Учитель руководит последовательностью защиты метода решения задачи №1с помощью системы уравнений с двумя переменными).

Составляем систему уравнений:

х + у = 600,

0,3х + 0,1у = 90; выразив из первого уравнения У через Х и подставив во второе уравнение полученный результат получим уравнение:

0,3х + 0,1 (600 - х) = 90

0,3х + 60 - 0,1х = 90

0,2х = 30

x = 30 / 0,2

x = 300 / 2

x = 150 (г) – масса 1 р-ра

Тогда y = 600 – x = 600 – 150 = 450 – масса 2 р-ра

Ответ: 150г.; 450г.

Учитель руководит последовательностью защиты метода решения задачи №1 математическим с помощью уравнения :

0,3х + 0,1 (600 - х) = 90

0,3х + 60 - 0,1х = 90

0,2х = 30

x = 30 : 0,2

x =300 : 2

x = 150 (г) – масса 1 р-ра

600 – 150 = 450 – масса 2 р-ра Ответ: 150г.; 450г.

Сравним решение задачи всеми способами. Кто может сделать вывод? (Учитель предлагает сделать

выводы. Организует обсуждение результатов.)

ВЫВОД: Разница в решении в том, что в математике - схема, а в химии – описание и формула расчёта, а уравнение для расчёта одно и то же. Может быть стоит совместить решения? А это будет выглядеть так:

В тетрадях пишем № задачи и перепишем обобщённую таблицу. Запишем уравнение:

0,3х + 0,1 (600 - х) = 90

и ответ: 150г.; 450г.

1.Выполняют задание №1 письменно, применяя последнюю обобщённую схему.

2.Делятся мнениями на поставленную проблему.

3.Работают с определением молярной массы и концентрации.

4.Делают выводы в выборе метода решения, в выборе схемы решения, учитывая знание формул по химии и химических обозначений.

ЭТАП 6. Новое, давно забытое старое. Или арифметический способ решения задач на растворы.

Существует ещё один способ решения задач такого типа – это арифметический способ. Этот способ более приближён к реальной жизни и его иногда называют «решение крестом».

Решим арифметическим методом задачу №1. Текст у вас есть. (Учитель, составляя схему решения данной задачи, читает каждую строчку. Комментирует каждую запись. Попутно отвечая на возникшие вопросы.)

Задача №1

Смешали 30%-ный раствор соляной кислоты с 10%-ным раствором и получили 600 г 15%-ного раствора. Сколько граммов каждого раствора было взято?

Решение:

Итак, читаем условие задачи №1 и составляем в тетради схему по условию задачи: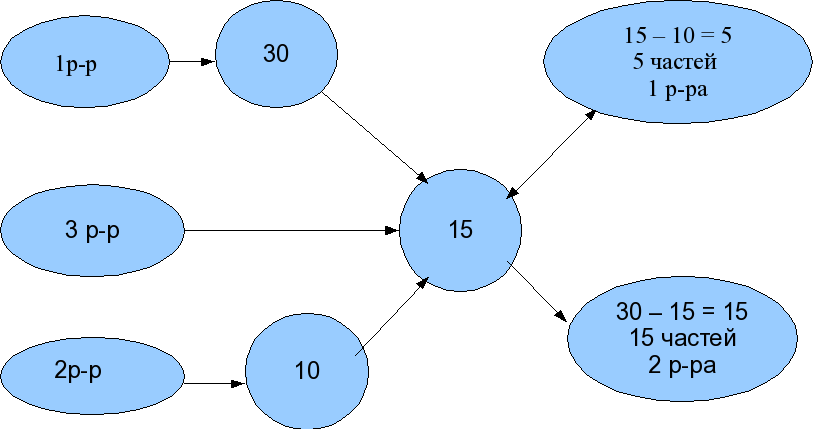

Числа 5 и 15 – это части! первого и второго растворов

Отношение 5 : 15 или, упрощая получим 1 : 3. Т.е. взяв 1 часть 1 р-ра и 3 части 2-го р-ра получим третий раствор нужной концентрации. Значит в третьем растворе массой 600 граммов 1 +3 = 4 части. Отсюда следует:

(600 : 4) * 1 = 150(г) – масса 1 раствора,

(600 : 4) * 3 = 450(г) – масса 2 раствора,

Ответ: 150г, 450г

Теперь читаем задачу №2 и, вместе со мной учимся записывать решение « крестом» этой задачи.

Итак, читаем условие задачи №2 (учитель просит ученика прочитать задачу) и составляем в тетради схему по условию задачи самостоятельно. А теперь проверим себя (учитель составляет схему пошагово для этой задачи):

1р-р 30 50 – 45 = 5(частей)

3 р-р 45

2 р-р 50 45 – 30 = 15(частей)

Числа 5 и 15 – это части! первого и второго р-ров

берём отношение 5 : 15 или 1 : 3.

Ответ: 1 : 3

1.Выполняют задание №1и №2 письменно, применяя предложенную схему арифметического решения.

2.Делятся мнениями. 3.Работают в парах.

4.Делают выводы в выборе решения для данного типа задач.

ЭТАП 7. Первичная проверка полученных результатов. Коррекция.

Наконец пришло время помочь Саше и Кате справиться с их проблемой. Их задачи – это №3, №4 на карточках.

Попробуем поработать в парах: по вариантам.

(учителя проверяют правильность решения тех, кто быстрее справился с заданием, и оценивают их)

А теперь обменяемся тетрадями, сверим решение и найдём ошибки:

Задача: Как из 78%-ной уксусной эссенции в домашних условиях приготовить 9%-ный уксус?

Решение:

1 р-р: 78%(эссенция) 9 – 0 = 9(частей)

3 р-р 9%

2 (р-р) вода 0% 78 – 9 = 69 (частей)

Итак 9 : 69 или 3 : 23. Ответ: 3 : 23.

Задача: Приготовить 980 граммов кислотного электролита для аккумулятора, имея 98% раствор серной кислоты H2SO4 . Сколько нужно взять воды H2O и серной кислоты H2SO4, чтобы получить 37%-ный раствор электролита?

Решение:

. H2SO4 98% 37 – 0 = 37(частей)

Электролит(980г) 37%

H2O 0% 98 – 37 = 61(частей)

980 : (37+61) * 37 = 980 : 98 * 37 = 370(г) - кислоты,

980 : 98 * 61 = 610(г) – воды

Ответ: 370г (H2SO4) , 610г (H2O).

Всё выполнено? Обратите внимание на последний пункт: поиск более простого решения задач. Да, мы познакомились с необычной схемой решения для одного из видов химических задач на растворы и смеси, схема «креста». Для других видов задач, может быть, вы придумаете или найдёте схемы сами? Всё в ваших руках.

Работа с карточками-заданиями: задачи №3 и №4.

ЭТАП 8. Информация о домашнем задании, инструктаж по его выполнению.

А теперь запишем домашнее задание: у каждого на столе лежат карточки с домашним заданием, положите в дневник. На обратной стороне листка написаны дополнительные

задания «для тех, кто хочет знать больше».

Задание:

1 уровень: на карточках две задачи - это для всех.

2 уровень: на карточках две задачи для более сильных.

ЭТАП 9. Рефлексия (Подведение итогов занятия)

Учитель: Мне хочется сказать вам дети, что вы все сегодня на уроке работали замечательно.

Сегодня кого нам хочется похвалить?… Я с вами согласна. В тетради некоторым из вас поставлены оценки за решение задач в самостоятельной работе. Я их выставила в журнал. Можете подать дневники. А кто хочет тоже себя похвалить пусть за самое маленькое, но открытие для себя, вам наши аплодисменты.

А кому сегодня не повезло, то повезёт потом, нужно только постараться.

А сейчас, ребята, я бы хотела узнать мнение об уроке. Для этого заполните, пожалуйста, листочки со смайликами и на переменке мне их на стол.

До свидания.

Приём «Смайлики»:

Суть - зафиксировать свои достижения на уроке:

Я понял…

Я пропускаю ход

Приложение:

Задания на карточке к уроку (на каждый стол):

1. Смешали 30%-ный раствор соляной кислоты с 10%-ным раствором и получили 600 г 15%-ного раствора. Сколько граммов каждого раствора было взято?

2. Смешали 30%-ный и 50%-ный растворы азотной кислоты и получили 45%-ный раствор. Найдите отношение массы 30%-ного раствора к массе 50%-ного раствора, взятых первоначально.

3. Задача: Приготовить 980 граммов кислотного электролита для аккумулятора, имея 98% раствор серной кислоты H2SO4 . Сколько нужно взять воды H2O и серной кислоты H2SO4, чтобы получить 37%-ный раствор электролита?

4. Задача: Как из 78%-ной уксусной эссенции в домашних условиях приготовить 9%-ный уксус?

Карточки с домашним заданиеь (на каждый стол):

1. Смешали 20%-ный раствор соляной кислоты с 40%-ным раствором и получили 800 г 25%-ного раствора. Сколько граммов каждого раствора было взято?

2. Смешали 75%-ный и 25%-ный растворы азотной кислоты и получили 40%-ный раствор. Найдите отношение массы 75%-ного раствора к массе 25%-ного раствора, взятых первоначально.

3. Задача: Приготовить 490 граммов кислотного электролита для аккумулятора, имея 49% раствор серной кислоты H2SO4 . Сколько нужно взять воды H2O и серной кислоты H2SO4, чтобы получить 20%-ный раствор электролита?

4. Задача: Как из 72%-ной уксусной эссенции в домашних условиях приготовить 8%-ный уксус?